Производная и дифференциал функции
Что такое производная
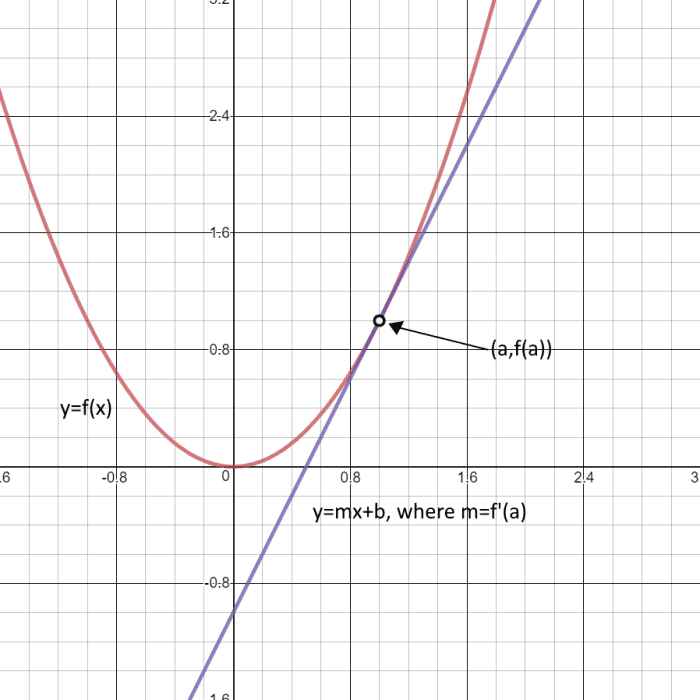
Производная функции — это одно из основных понятий математики. Производные измеряют мгновенную скорость изменения в точке. Мгновенная скорость изменения функции в точке равна наклону касательной линии в этой точке. Скорость изменения можно оценить, вычислив отношение изменения функции Δy к изменению независимой переменной Δx. В определении производной это отношение рассматривается в пределе при Δx → 0.
Например, наклон прямой, определяющий скорость ее изменения, постоянен на всем ее протяжении. Производная позволяет узнать, каков наклон параболы в конкретной точке, поскольку наклон параболы колеблется.
Производную от f(x) чаще всего обозначают \(f'(x) или df/dx\), и она определяется следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(f'(x) = lim (f(x+h) - f(x))/h\)
Предел — это предел для h, переходящий в 0.
Нахождение производной функции называется дифференцированием. Вычисляется наклон прямой, проходящей через f в точках x и x+h. Поскольку мы берем предел для h равным 0, эти точки будут лежать бесконечно близко друг к другу; следовательно, это наклон функции в точке x. Этот предел не обязательно существует. Если он существует, то функция дифференцируема; если нет, то функция не дифференцируема.
Что такое дифференциал
Дифференцирование функции — это способ показать скорость изменения функции в данной точке. Для вещественных функций это наклон касательной линии в точке графика.
Производная y по x определяется как изменение y по сравнению с изменением x, когда расстояние между x0 и x1 становится бесконечно малым (бесконечно малым). Производная часто записывается как \(dy/dx.\)
Говоря математическим языком, если f — вещественная функция, a — точка в ее области определения, то производная f в точке a определяется следующим образом:
\(f'(a) = lim h→0 ((f(a+h)-f(a) / h)\)
Отличия
Дифференциал и производная тесно связаны друг с другом. Дифференциальные уравнения описывают связь между переменными и их производными. Нахождение производной — это процесс дифференцирования.
- Основное различие между дифференциалом и производной заключается в том, что производная относится к скорости изменения функции, а дифференциал — к фактическому изменению функции.
- Другой способ определить производные — рассмотреть соотношение дифференциалов функции и переменной.
- Еще одно различие между дифференциалом и производной заключается в том, что дифференциал — это изменение переменной (dx). В отличие от этого, производная — это изменение функции (dy/dx) (dy/dx) (dx).
- Производная — это отношение дифференциалов, поскольку функция представляет собой связь между двумя переменными. Дифференциалы показывают фактическое изменение значения через линейное отображение, тогда как производные представляют то же самое изменение через карту наклона.
Как найти производную и дифференциал функции
Вычисление производной
Первый способ вычислить производную функции — это просто вычислить ее предел. Если он существует, значит, у вас есть производная, иначе вы знаете, что функция не дифференцируема.
Пример:
В качестве функции возьмем f(x) = x2.
\((f(x+h)-f(x))/h = ((x+h)2 - x2)/h = (x2 + 2xh +h2 - x2)/h = 2x + h\)
Теперь нам нужно взять предел для h, чтобы увидеть 0:
f'(x) = 2x.
Вычисление производной функции может стать намного проще, если использовать некоторые свойства:
Правило суммы: (af(x)+bg(x))' = af'(x) + bg'(x)
Правило квотирования: (f(x)/g(x))' = (f'(x)g - f(x)g'(x))/g(x)2
Правило произведения: (f(x)g(x))' = f'(x)g(x) + f(x)g'(x)
Правило цепочки: f(g(x))' = f'(g(x))g'(x)
Источник: owlcation.com
Производная встречается во многих математических задачах. Примером может служить нахождение касательной к линии функции в определенной точке. Чтобы получить наклон этой линии, понадобится производная для нахождения наклона функции в этой точке.
Источник: owlcation.com
Другое применение — поиск экстремальных значений функции, то есть (локального) минимума или максимума функции. Поскольку в минимуме функция находится в точке минимума, наклон переходит от отрицательного значения к положительному. Поэтому производная равна нулю в минимуме и наоборот: она также равна нулю в максимуме.
Многие физические явления описываются дифференциальными уравнениями. В этих уравнениях есть производные, а иногда и производные более высокого порядка (производные производных). Решение этих уравнений позволяет многое узнать, например, о динамике жидкостей и газов.
Знание следующих правил облегчит расчет производных.
Многочлены
Многочлен — это функция вида a1 xn + a2xn-1 + a3 xn-2 + ... + anx + an+1.
Таким образом, многочлен — это сумма нескольких членов вида axc. Поэтому по правилу суммы, если мы теперь имеем производную каждого члена, мы можем просто сложить их, чтобы получить производную многочлена. Этот случай известен, и мы его получили: d/dx xc = cxc-1
Тогда производная многочлена будет: na1 xn-1 + (n-1)a2xn-2 + (n-2)a3 xn-3 + ... + an
Экспоненты и логарифмы
Экспоненциальная функция ex обладает тем свойством, что ее производная равна самой функции. Поэтому: d/dx ex = ex
Найти производную других степеней e можно с помощью цепного правила. Например, \(e2x^2\) — это функция вида f(g(x)), где f(x) = ex и g(x) = 2x2. Тогда производная по правилу цепочки становится равной 4x \(e2x^2\).
Если основанием экспоненциальной функции является не e, а другое число a, то производная будет другой.
d/dx ax = ax ln(a), где ln(a) — натуральный логарифм от a.
Производная логарифма 1/x в случае натурального логарифма и 1/(x ln(a)) в случае логарифма с основанием a.
Отрицательные и дробные числа
d/dx xc = cxc-1 выполняется и в том случае, если c — отрицательное число, поэтому, например:
1/x = x-1
d/dx 1/x = -1/x2
Более того, она справедлива и при дробном c. Это позволяет нам вычислять производную, например, квадратного корня:
\(d/dx sqrt(x) = d/dx x1/2 = 1/2 x-1/2 = 1/2sqrt(x)\)
Гониометрические функции
Синус, косинус и тангенс также имеют производную.
d/dx sin(x) = cos(x)
d/dx cos(x) = - sin(x)
d/dx tan(x) = 1 - tan2(x)
d/dx arcsin(x) = 1/sqrt(1-x2)
d/dx arccos(x) = -1/sqrt(1-x2)
d/dx arctan(x) = 1/(1+x2)
Вычисление дифференциала
Предположим, что существует функция f(x) = x2. Наклон этой функции в определенной точке, скажем, 3, можно определить с помощью дифференциального исчисления. Производная этой функции будет f'(x) = 2x. Подставив в это уравнение x = 3, получим f'(x) = 6. Таким образом, наклон касательной линии при x = 3 равен 6.
Различные формулы дифференциального исчисления используются для нахождения производных различных типов функций. Согласно определению, производная функции может быть определена следующим образом:
\(f'(x) = limh→0 f(x+h)-f(x) / h\)
Ниже приведены важные формулы дифференциального исчисления для различных функций:
Элементарные:
d/dx ex = ex
d/dx ax = ax. ln .a , где a > 0, a ≠ 1
d/dx ln x = 1/x, x > 0
d/dx √x = 1/(2 √x)
Гиперболические:
d/dx sinhx = coshx
d/dx coshx = sin hx
d/dx tan hx = sec h2x
d/dx cot hx = -cosec h2x
d/dx sec hx = -sech hx tan hx
d/dx cosec hx = -cosec hx cot hx
Тригонометрические:
d/dx sin x = cos x
d/dx cos x = -sin x
d/dx tan x = sec2 x , x ≠ (2n + 1) π / 2 , n ∈ I
d/dx cot x = - cosec2 x, x ≠ nπ, n ∈ I
d/dx sec x = sec x tan x, x ≠ (2n + 1) π / 2 , n ∈ I
d/dx cosec x = - cosec x cot x, x ≠ nπ, n ∈ I
Примеры решения задач
Примеры дифференциального исчисления:
f(x) = x3
Решение:
Известно, d(xn) / dx = n xn-1
Следовательно, f'(x) = dx3 /dx
f'(x)= 3 x3-1
f'(x)= 3 x2
Найдите дифференциал функции y = sin x - x cos x
Решение:
Определите производную заданной функции: y' = (sin x - x cos x)' = cos x - (x' cos x + x (cos x)') = cos x - (cos x + x (-sinx)) = cos x - cos x + x sin x = x sin x.
Дифференциал имеет следующий вид: dy = y'dx - x sin x dx.
f(x) = 3x2-2x+1
Решение:
Дано f(x) = 3x2-2x+1
Дифференцируя обе стороны, получаем:
f'(x) = 6x - 2, где f'(x) — производная от f(x).
Вычислите dy и Δy, если y = cos(x2+1)-x, также x меняет значение от x = 2 на x = 2.03.
Решение: Сначала вычислим реальное изменение y, Δy.
Δy = cos((2.03)2+1)-2.03-(cos(22+1)-2) = 0.083581127
Теперь получим формулу для dy.
dy=(-2xsin(x2+1)-1)dx
Далее, вычтем x = 2 от x = 2.03, получим Δx=0.03.
Поэтому мы предполагаем, что dx≈Δx=0.03.
dy = (-2(2)sin(22+1)-1)(0.03) = 0.085070913
Мы видим, что на самом деле имеем Δy≈dy при условии, что мы сохраняем значение Δx небольшим.
Примеры вычисления производной:
Найдите производную от x6+x3+2.
Решение:
(d/dx)x6 = 6x5
(d/dx)x3 = 3x2
(d/dx)2 = 0
Следовательно, производная x6+x3+2 = 6x5+3x2
Если f(x) = logx (logx), то f′(x) при x = e — это _____.
Решение:
f(x) = logx (logx)
= log (log x) / logx
f′(x)= 1 / x - 1 / x log (logx) / (logx)2
⇒ f′(e) = [1 / e - 0] / 1
Чему равен дифференциальный коэффициент ax + log x . sinx?
Решение:
Пусть y = ax + log x . sinx
Дифференцируя по x, получаем
dy / dx = ax loge(a) + (1 / x) sin x + log x . cos x
= 1 / e
Используя определение предела, найдите производную функции f(x) = 3x + 2.
Решение:
Запишите приращение функции: Δy = y(x+Δx)-y(x) = [3(x+Δx)+2] - [3x+2] = 3x+3Δx+2-3x-2 = 3Δx.
Коэффициент разности равен:
Δy/Δx = 3Δx/Δx = 3.
Тогда производная имеет вид:
f'(x) = lim Δx→0 Δy/Δx = lim Δx→0 3 = 3.
Используя определение производной, докажите, что производная от константы равна 0.
Решение:
В данном случае функция y (x) всегда равна константе C. Поэтому мы можем записать: y (x) = C, y (x+Δx) = C.
Приращение функции тождественно равно нулю: Δy = y(x+Δx) - y(x) = C - C ≡ 0.
Подставляя это в предельное определение производной, получаем:
y'(x) = lim Δx→0 Δy/Δx = lim Δx→0 y(x+Δx)-y(x) / Δx = lim Δx→0 0/Δx = lim Δx→0 =0.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так