Уравнение директрисы параболы
Что такое директриса параболы
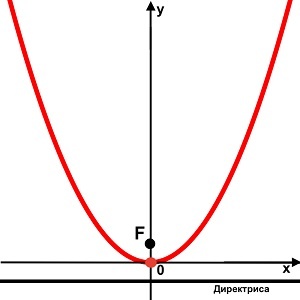
Директриса параболы — такая прямая, кратчайшее расстояние от которой до любой точки, принадлежащей параболе, точно такое же, как расстояние от этой точки до фокуса.
Вершина параболы — точка пересечения параболы с ее осью. Она считается началом системы координат, канонической для данной кривой.
Вершина — середина перпендикуляра, опущенного из фокуса на директрису. Таким образом, директриса перпендикулярна оси симметрии и проходит на расстоянии р/2 от вершины параболы. Число р — фокальный параметр, расстояние от фокуса до директрисы. Поскольку все параболы подобны, именно эта характеристика определяет масштаб конкретной параболы.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Каноническое уравнение параболы
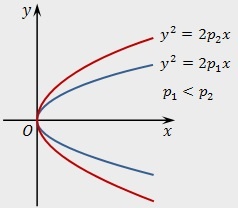
Каноническое уравнение параболы:
\(y^2\;=\;2px\)
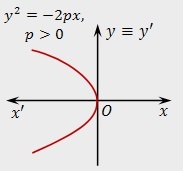
Если расположить параболу слева от оси ординат, уравнение примет вид:
\(y^2\;=\;-\;2px\)
Уравнение директрисы параболы, если вершина не в пересечении осей координат
Формула директрисы параболы имеет вид:
\(х\;=\;-\frac р2\)
Если вершину перенести в точку \((x_0;\;y_0)\), отличную от начала осей координат, каноническое уравнение примет вид:
\({(y\;-\;y_0)}^2\;=\;2p\;\times\;(x\;-\;x_0)\)
Алгоритм расчета
- Если уравнение параболы приведено в виде квадратного многочлена, перенесем все слагаемые с y в левую часть уравнения, а с х — в правую.
- Упростим выражение, выделив полный квадрат относительно одной из переменных.
- Введем новые переменные \((x_1;\;y_1)\), чтобы привести уравнение к каноническому виду, ведя при этом отсчет с новой точки начала координат.
- Вычислим параметр р и фокус, запишем уравнение директрисы.
- Вернемся к старым координатам, заменив \((x_1;\;y_1)\) на х и y.
Фокус параболы
Расстояние от точки фокуса (F) до любой точки параболы равняется расстоянию от этой точки к директрисе.
Чтобы составить уравнение директрисы, нужно знать фокальный параметр.
Фокальный параметр — половина длины хорды, проходящей через её фокус перпендикулярно фокальной оси.
Примеры решения задач
Задача №1
Составить уравнение директрисы параболы \(y^2\;=\;6x\).
Решение
Сравнив каноническое уравнение с данным, получим:
\(2р = 6 \)
\(р = 3\)
\(\frac р2\;=\;\frac32\)
Уравнение директрисы — \(х\;=\;-\frac р2.\)
В данном случае оно будет выглядеть так:
\(х\;=\;-\;\frac32\)
Задача №2
Найти директрису параболы, заданной уравнением \(4х^2\;-\;12х\;+\;y\;+\;6\;=\;0.\)
Решение
Преображаем многочлен, находим полный квадрат относительно переменной х:
\(4х^2\;-\;12х\;+\;y\;+\;6\;=\;0\;\Rightarrow\;4(х^2\;-\;3х)\;+\;y\;+\;6\;=\;0\;\Rightarrow\;\;4((х^2\;-\;2\;\times\frac32х\;+\;\frac94)\;-\;\frac94)\;+\;y\;+\;6\;=\;0\;\Rightarrow\;\)
\(\;\Rightarrow\;(4\;{(х\;-\;\frac32)}^2\;-\;9\;+\;y\;+\;6\;=\;0\;\Rightarrow\;y\;-\;3\;=-\;4\;{(х\;-\;\frac32)}^2\;\Rightarrow\;{(х\;-\;\frac32)}^2\;=\;-\;\frac14\;(y\;-\;3)\)
Пусть \((y — 3)\) будет \(y_1\), а \((х\;-\;\frac32)\) — \(х_1\).
Тогда, перенеся начало координат в точку \((x_1;\;y_1)\), получим каноническое уравнение \(х_1^2\;=\;-{\textstyle\frac14}y_1\).
\(2р\;=\;\frac14\;\Rightarrow\;р\;=\;\frac18\;\Rightarrow\;\frac р2\;=\;\frac1{16}\)
Тогда уравнение директрисы — \(y_1=\;\frac1{16}\).
Заменив \(y_1\) на \((y — 3)\), получим уравнение: \(y\;–\;3\;=\;\frac1{16}\)
Следовательно, \(y\;–\;\frac{49}{16}\;=\;0\).
В старой системе координат уравнение директрисы:
\(16у — 49 = 0, у\;=\;\frac{49}{16}\).
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так