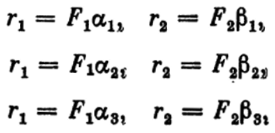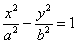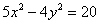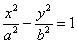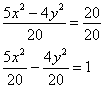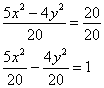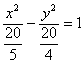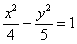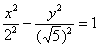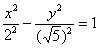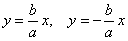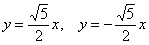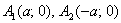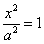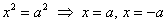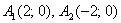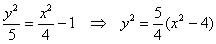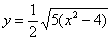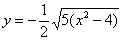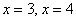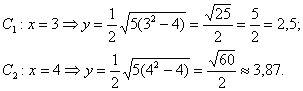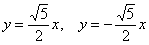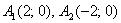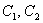Способы построения гиперболы самостоятельно
Гипербола в математике — что это такое
Гипербола представляет собой линию, определяемую в некой декартовой прямоугольной системе координат каноническим уравнением:
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1.\label{ref9}\)
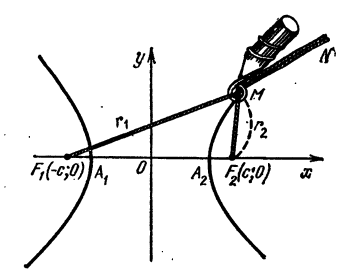
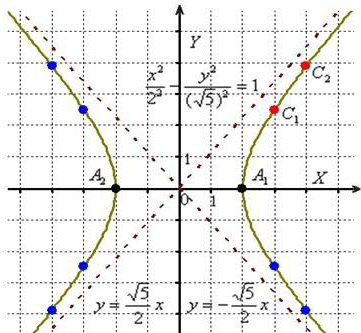
Согласно записанному правилу, все точки гиперболы \(|x| \geq a\). Таким образом, данные точки расположены за пределами вертикальной полосы ширины \(2a\), как показано на рисунке. Ось абсцисс канонической системы координат имеет точки пересечения с гиперболой. Координаты этих точек соответствуют: \((a, 0)\) и \((-a, 0)\). Такие точки называют вершинами гиперболы.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Ось ординат не имеет общих точек с гиперболой. В состав гиперболы входят две части, которые не связаны между собой. Они носят название ветвей гиперболы. Числа «a» и «b» являются соответственно вещественной и мнимой полуосями гиперболы.
Ветви гиперболы — это две отдельные кривые, из которых состоит гипербола.
Ближайшие друг к другу точки двух ветвей гиперболы являются вершинами гиперболы.
Большая ось гиперболы — наименьшее расстояние между двумя ее ветвями.
Центр гиперболы — это середина ее большой оси.
Большая полуось гиперболы — расстояние, на которое удалены центр и одна из вершин, обозначается «а».
Фокальное расстояние гиперболы — расстояние, на которое удалены друг от друга центр и один из фокусов, обозначается «с».
Оба фокуса гиперболы расположены на продолжении большой оси и равноудалены от центра гиперболы.
Прямая, включающая в себя большую ось гиперболы, носит название действительной, или поперечной, оси гиперболы.
Прямая в виде перпендикуляра к действительной оси, которая пересекает центр гиперболы — мнимая, или сопряженная ось гиперболы.
Отрезок между фокусом гиперболы и гиперболой, который перпендикулярен к действительной оси, — это фокальный параметр.
Прицельный параметр — расстояние от фокуса до асимптоты гиперболы, обозначается «b».
Перицентрическое расстояние — расстояние, на которое фокус удален от ближайшей вершины гиперболы, обозначается \({\displaystyle r_{p}}r_{p}\).
Перечисленные характеристики гиперболы взаимосвязаны. Справедливы следующие соотношения:
- \({\displaystyle c^{2}=a^{2}+b^{2}}{\displaystyle c^{2}=a^{2}+b^{2}}\)
- \({\displaystyle \varepsilon =c/a}{\displaystyle \varepsilon =c/a}\)
- \({\displaystyle b^{2}=a^{2}\left(\varepsilon ^{2}-1\right)}{\displaystyle b^{2}=a^{2}\left(\varepsilon ^{2}-1\right)}\)
- \({\displaystyle r_{p}=a\left(\varepsilon -1\right)}{\displaystyle r_{p}=a\left(\varepsilon -1\right)}\)
- \({\displaystyle a={\frac {p}{\varepsilon ^{2}-1}}}{\displaystyle a={\frac {p}{\varepsilon ^{2}-1}}}\)
- \({\displaystyle b={\frac {p}{\sqrt {\varepsilon ^{2}-1}}}}{\displaystyle b={\frac {p}{\sqrt {\varepsilon ^{2}-1}}}}\)
- \({\displaystyle c={\frac {p\varepsilon }{\varepsilon ^{2}-1}}}{\displaystyle c={\frac {p\varepsilon }{\varepsilon ^{2}-1}}}\)
- \({\displaystyle p={\frac {b^{2}}{a}}}p={\frac {b^{2}}{a}}\)
Оси симметрии гиперболы представляют собой оси канонической системы координат, а начало канонической системы является центром симметрии.
Когда требуется исследовать форму гиперболы, следует начать с поиска ее пересечения с произвольной прямой, пересекающей начало координат. Уравнение прямой можно задать в виде:
\(y=kx\)
Такой выбор связан с тем, что прямая \(x=0 \) не пересекает гиперболу. Абсциссы точек пересечения можно вычислить с помощью уравнения:
\(\frac{x^{2}}{a^{2}}-\frac{k^{2}x^{2}}{b^{2}}=1\)
Таким образом, при \(b^{2}-a^{2}k^{2} > 0\) получим:
\(x=\pm \frac{ab}{\sqrt{b^{2}-a^{2}k^{2}}}\)
Полученное равенство позволит рассчитать координаты точек пересечения:
\((ab/v, abk/v)\)
\((-ab/v, -abk/v)\)
В данном случае:
\(v=(b^{2}-a^{2}k^{2})^{1/2}\)
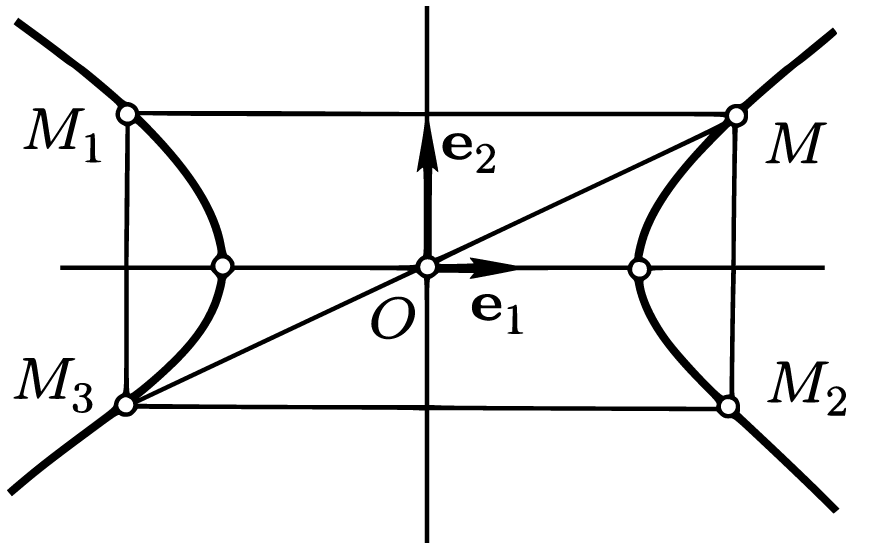
Руководствуясь свойством симметрии, можно проанализировать смещение первой из точек при изменении k, как показано на рисунке.
Числитель дроби \(ab/v\) является постоянной величиной, а знаменатель характеризуется максимальным значением, если \(k=0\). Таким образом, самую маленькую абсциссу имеет вершина \((a, 0)\). При увеличении \(k \) знаменатель убывает, и x растет, стремясь к бесконечности, когда k приближается к числу \(b/a\).
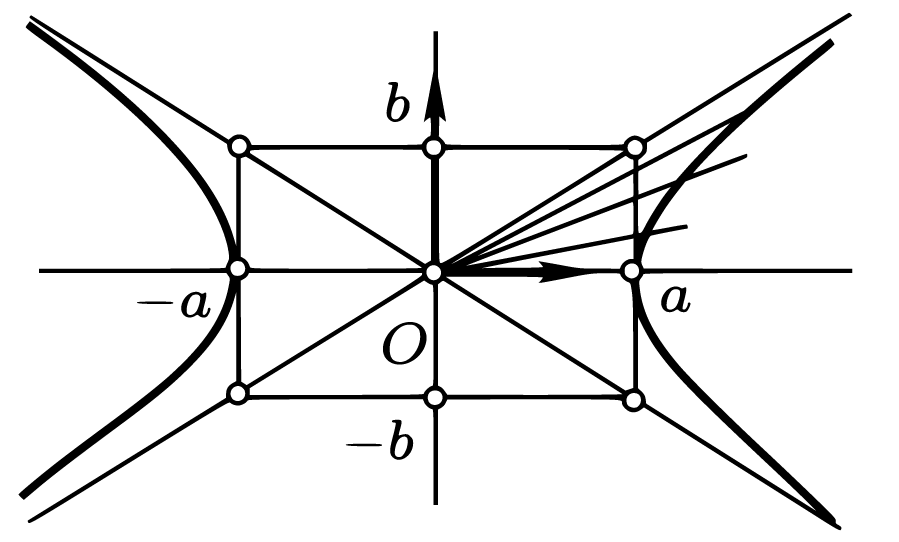
Прямая \(y=bx/a\) с угловым коэффициентом \(b/a\) не имеет точек пересечения с гиперболой, как и прямые с большими угловыми коэффициентами. Какая-либо прямая, обладающая меньшим положительным угловым коэффициентом, пересекает гиперболу.
При сдвиге прямой от горизонтального положения по часовой стрелке, k будет уменьшаться, \(k^{2}\) — увеличиваться, и прямая будет иметь удаляющиеся точки пересечения с гиперболой до тех пор, пока не займет положения с угловым коэффициентом \(-b/a\).
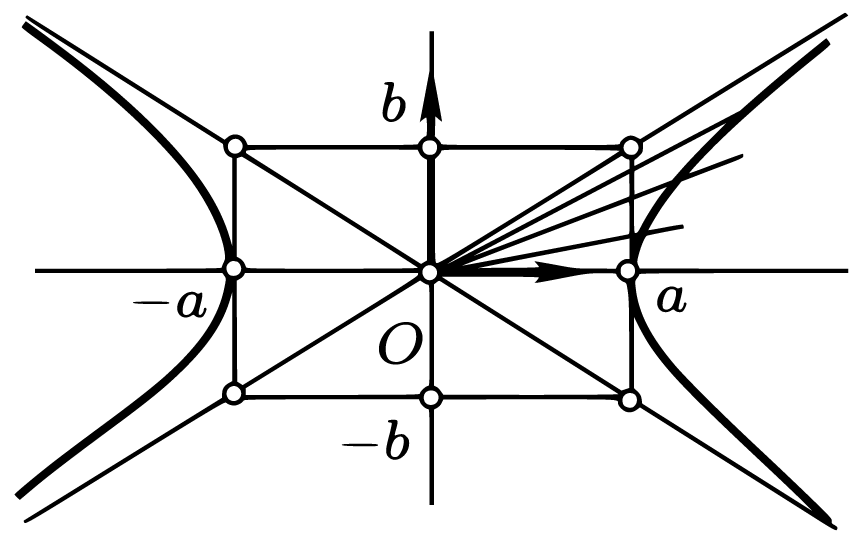
К прямой \(y=-bx/a\) относится все, что было сказано о \(y=bx/a\): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из вышесказанного следует вывод, что гипербола имеет вид, изображенный на рисунке.
Асимптоты гиперболы являются прямыми, описываемыми уравнениями \(y=bx/a\) и \(y=-bx/a \) в канонической системе координат.
Предположим, что уравнения асимптот имеют вид:
\(bx-ay=0\)
\(bx+ay=0\)
Расстояния от точки \(M(x, y)\) до асимптот составят
\(h_{1}=\frac{|bx-ay|}{\sqrt{a^{2}+b^{2}}},\)\(\ h_{2}=\frac{|bx+ay|}{\sqrt{a^{2}+b^{2}}}\)
В том случае, когда точка M расположена на гиперболе:
\(b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2}\)
\(h_{1}h_{2}=\frac{|b^{2}x^{2}-a^{2}y^{2}|}{a^{2}+b^{2}}=\frac{a^{2}b^{2}}{a^{2}+b^{2}}\)
Произведение расстояний от точки гиперболы до асимптот является постоянным и соответствует \(a^{2}b^{2}/(a^{2}+b^{2})\).
Из данного определения можно вывести ключевое свойство, которым обладают асимптоты гиперболы.
В том случае, когда точка совершает движение по гиперболе таким образом, что ее абсцисса по абсолютной величине неограниченно возрастает, расстояние от точки до одной из асимптот стремится к нулю.
В действительности получим, что хотя бы одно из расстояний \(h_{1}\) или \(h_{2}\) при этих условиях должно неограниченно увеличиваться. Если предположить, что утверждение не справедливо, то произведение не было бы постоянной величиной.
Введем такое число с, что:
\(c^{2}=a^{2}+b^{2}\)
и \(c > 0\)
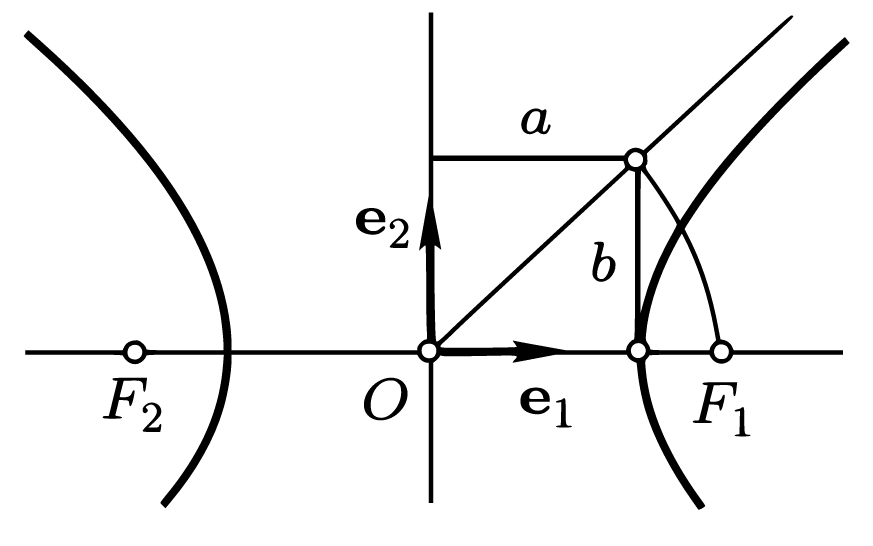
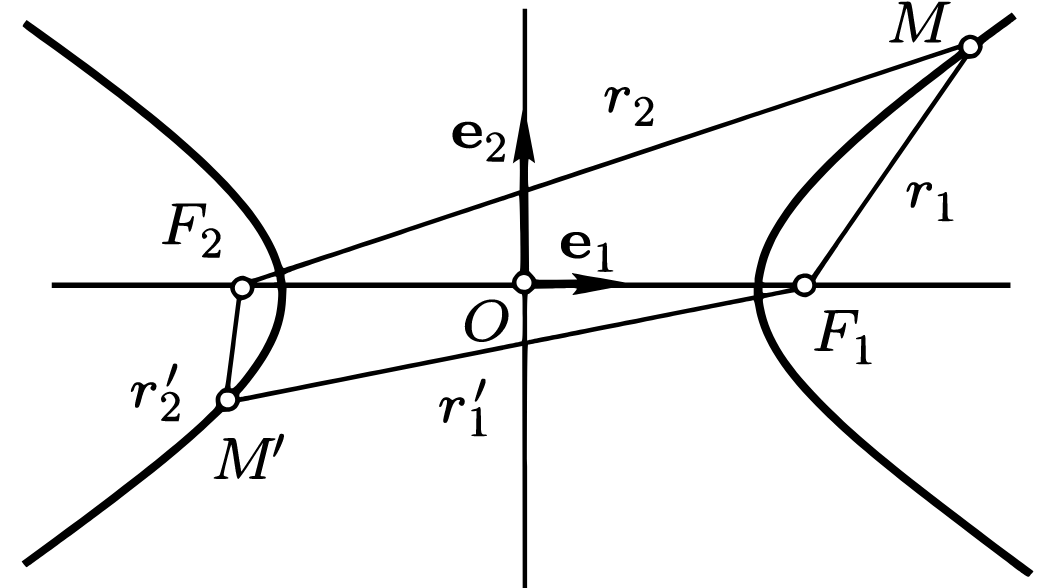
Фокусы гиперболы — точки \(F_{1}\) и \(F_{2}\) с координатами \((c, 0)\) и \((-c, 0)\) в канонической системе координат.
Отношение \(\varepsilon=c/a\), как и для эллипса, называется эксцентриситетом. У гиперболы \(\varepsilon > 1\).
Расстояния от произвольной точки \(M(x, y)\) на гиперболе до каждого из фокусов определяются абсциссой \(x\):
\(r_{1}=|F_{1}M|=|a-\varepsilon x|,\ r_{2}=|F_{2}M|=|a+\varepsilon x|\)
Следует отметить, что равенства \eqref{ref11} можно представить в более подробной форме:
- для правой ветви гиперболы \((x \geq a): r_{1}=\varepsilon x-a\), \(\ r_{2}=\varepsilon x+a\);
- для левой ветви гиперболы \((x \leq -a): r_{1}= a-\varepsilon x\), \(\ r_{2}=-\varepsilon x-a\).
Таким образом, для правой ветви \(r_{2}-r_{1}=2a\), а для левой ветви \(r_{1}-r_{2}=2a\). В обоих случаях:
\(|r_{2}-r_{1}|=2a\)
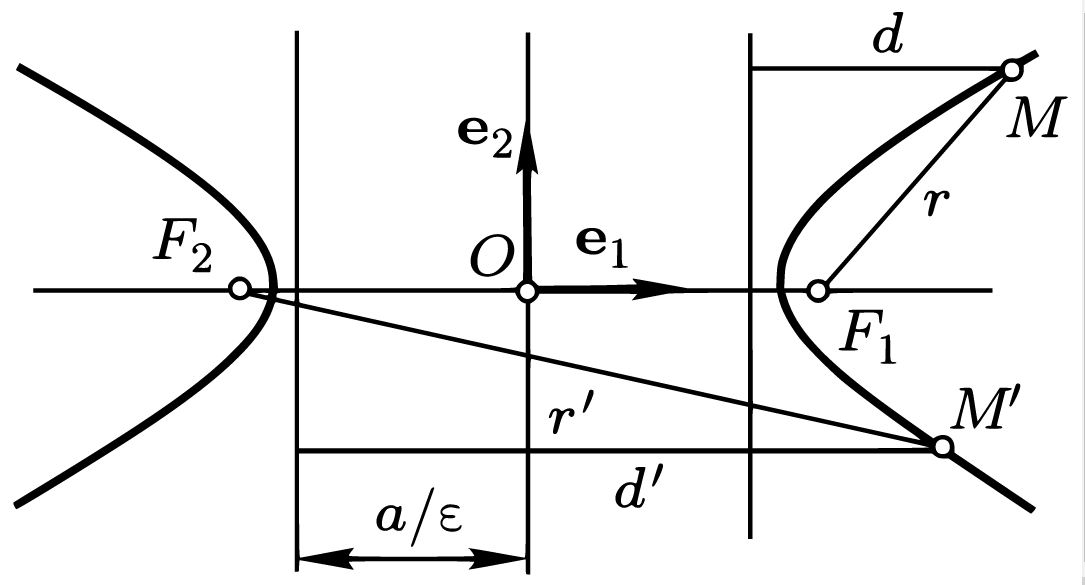
Директрисы гиперболы — прямые, заданные в канонической системе координат уравнениями: \(x=\frac{a}{\varepsilon}\), \(\ x=-\frac{a}{\varepsilon}\).
Директрисы расположены поблизости от центра в отличие от вершин. Из этого можно сделать вывод, что директрисы не имеют точек пересечения с гиперболой. Директриса и фокус, которые расположены по одну сторону от центра, считаются соответствующими друг другу.
Для того чтобы точка \(M\) была расположена на гиперболе, необходимо и достаточно, чтобы разность ее расстояний до фокусов по абсолютной величине равнялась вещественной оси гиперболы 2a.
С целью доказательства достаточности данного условия его следует записать в виде:
\(\sqrt{(x-c)^{2}+y^{2}}=\pm 2a+\sqrt{(x+c)^{2}+y^{2}}\)
Следующие действия отличаются от доказательства соответствующего утверждения для эллипса только тем, что нужно воспользоваться равенством:
\(c^{2}=a^{2}+b^{2}\), а не \(c^{2}=a^{2}-b^{2}\)
Для того чтобы точка была расположена на гиперболе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету \(\varepsilon\).
Можно доказать, к примеру, необходимость условия для фокуса \(F_{2}(-c, 0).\) Предположим, что \(M'(x, y)\) является точкой гиперболы. Расстояние от \(M’\) до директрисы с уравнением \(x=-a/\varepsilon\) равно:
\(d’=\left|x+\frac{a}{\varepsilon}\right|=\frac{1}{\varepsilon}|\varepsilon x+a|\)
Таким образом:
\(r’/d’=\varepsilon\).
Уравнение касательной к гиперболе в точке \(M_{0}(x_{0}, y_{0})\), которая принадлежит данной гиперболе, можно записать так же, как подобное уравнение в случае эллипса. Уравнение касательной к гиперболе:
\(\frac{xx_{0}}{a^{2}}-\frac{yy_{0}}{b^{2}}=1\)
Касательная к гиперболе в точке \(M_{0}(x_{0}, y_{0})\) представляет собой биссектрису угла между отрезками, которые соединяют рассматриваемую точку с фокусами.
Как построить гиперболу самостоятельно
Построение графика гиперболы следует начать с изображения прямоугольной системы координат Декарта. Алгоритм действий:
- На листе бумаги нарисовать горизонтальную прямую. Выполнить действие следует таким образом, чтобы конец прямой с правой стороны был обозначен с помощью стрелки. Данная прямая является осью \(X\) и носит название абсциссы.
- На середине оси \( Х\) необходимо опустить перпендикуляр. Конец полученной прямой в верхней части нужно обозначить стрелкой. В результате получена ось \(Y\), которую называют ординатой.
- На следующем шаге необходимо пронумеровать шкалу. С правой стороны на оси \(Х\) расположены положительные значения \(Х\) в порядке возрастания — от 1 и выше. С левой стороны — отрицательные. В верхней части на оси \(Y\) расположены положительные значения \(Y\) в порядке возрастания. В нижней части — отрицательные.
Точка, в которой пересекаются абсцисса и ордината является началом координат, то есть числом 0. От данной точки следует откладывать все значения \(Х\) и \(Y\).
С помощью прямоугольной системы координат плоскость поделена на четыре части, которые называют четвертями и нумеруют против часовой стрелки. Для того чтобы построить график, требуется определить точки. Каждая точка координатной плоскости определяется парой чисел \((x;y)\). Данные числа представляют собой координаты точки, где:
- \(х\) — абсцисса точки;
- \(y\) — ордината.
Гипербола представляет собой график функции, которая задана формулой:
\(y=k/x\)
где \(k\) — является каким-то коэффициентом, не равным нулю;
\(x\) — представляет собой независимую переменную.
Гипербола включает в себя две части, расположенные симметрично в разных четвертях. Данные части носят название ветвей гиперболы. При \(k>0\), ветви расположены в 1 и 3 четвертях. При \(k<0\), ветви гиперболы размещены во 2 и 4 четвертях.
Принцип построения гиперболы можно рассмотреть на примере, когда функция задана следующей формулой:
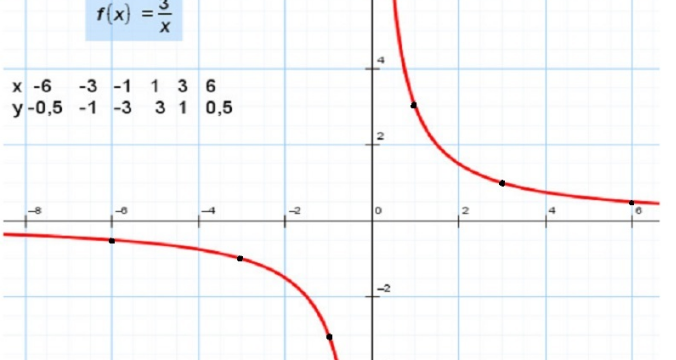
\(y=3/х\)
Так как коэффициент 3 обладает положительным значением, гипербола, соответственно, будет находиться в 1 и 3 четвертях. Можно взять произвольно значения \(Х\) и найти значения \(Y\). Таким образом, получатся координаты точек, с помощью которых можно изобразить гиперболу. Важно отметить, что \(Х\) не должно иметь нулевое значение, так как на 0 делить нельзя.
Поскольку мы знаем, что гипербола располагается в двух четвертях, то берем как положительные значения, так и отрицательные. Предположим, что \(Х\) равен: -6, -3, -1, 1, 3, 6. Далее можно рассчитать ординаты путем подстановки каждого значение \(Х\) в начальную формулу:
\(y=3/-6\)
\(у=3/-3\)
\(у=3/-1\)
\(у=3/1\)
\(у=3/3\)
\(у=3/6\)
В результате, значения \( Y\) равны: -0.5, -1, -3, 3, 1, 0.5.
Полученные 6 точек с координатами необходимо отложить на системе координат. Далее точки соединяют с помощью кривых линий, как изображено на рисунке. В итоге получилась гипербола.
Построение гиперболы по фокусам
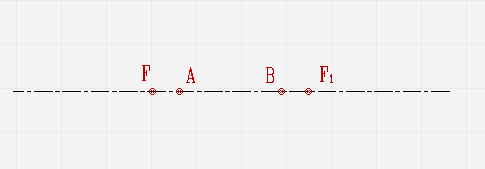
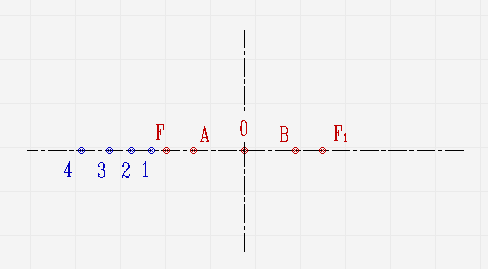
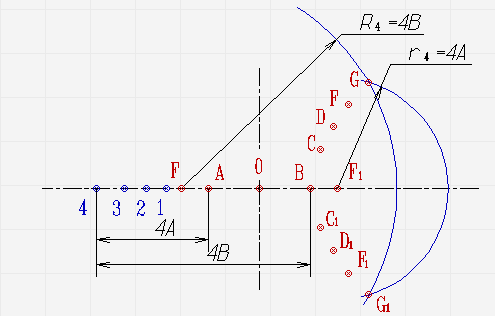
Гиперболу можно построить, зная заданные вершины \(А\) и \(В\) и фокусное расстояние \(FF1\). Алгоритм построения следующий:
- В первую очередь фокусное расстояние следует разделить пополам, чтобы получить точку 0.
- Далее с левой стороны от фокуса \(F\) можно отметить ряд произвольных точек 1, 2, 3, 4 и так далее, расстояние между которыми постепенно увеличивается.
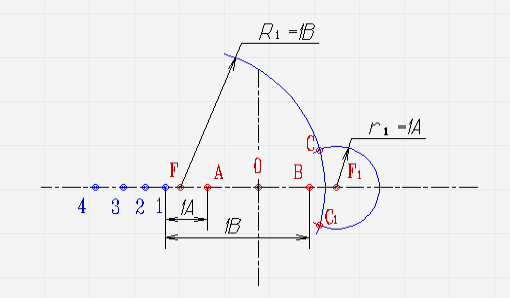
- Затем нужно начертить вспомогательные окружности с центром в фокусе \(F\), имеющие радиусы \(R1=1B\), \(R2=2B\), \(R3=3B\), \(R4=4B\) и так далее.
- На следующем этапе можно изобразить вспомогательные окружности с центром в фокусе \(F1\) и радиусами \(r1=1A\), \(r2=2A\), \(r3=3A\), \(r4=4A\) и так далее.
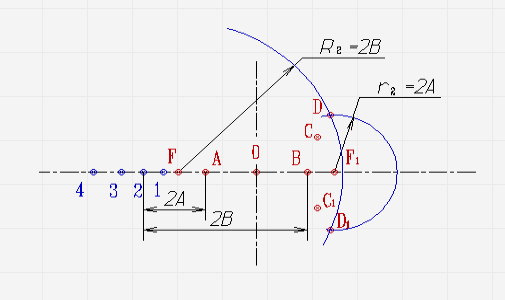
- При пересечении вспомогательных окружностей определяется положение точек гиперболы. \(С\), \(С1 \)представляют собой точки, которые образованы в результате пересечения окружностей радиусов \(R1\) и \(r1\). Точки \(D,D1\) являются точками, в которых пересекаются окружности \(R2\) и \(r2\).
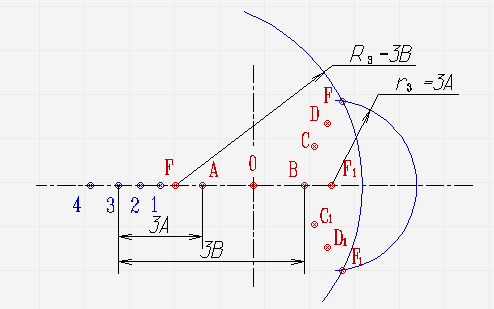
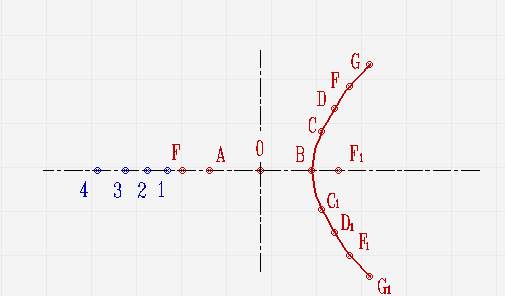
- Полученные точки остается соединить с помощью плавной кривой линии, чтобы получить правую ветвь гиперболы.
- Аналогичным способом следует выполнить построение левой ветви гиперболы.
Как построить гиперболу по точкам
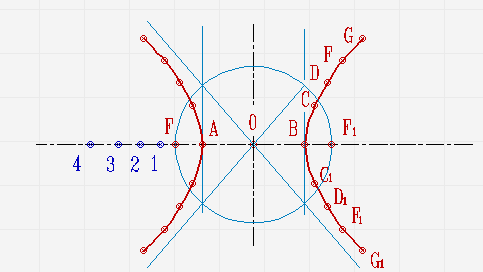
Исходя из определения гиперболы, разница между расстояниями \(r1\) и \(r2\) для всех ее точек является постоянной величиной. Таким образом, переход от одной точки гиперболы к другой осуществляется путем увеличения или уменьшения данных характеристик. Алгоритм действий:
- В первую очередь следует отложить точки \(А1\) и \(А2\). Точка \( А2\) является точкой касания двух окружностей, центр одной из которых расположен в фокусе \( F1\), а радиус составляет F1A2. Другая окружность обладает центром в фокусе \(F2\) и радиусом \(F2A2\).
- Следующие точки гиперболы можно определить при пересечении пар окружностей с радиусами, которые равны:
Таким образом, новые значения радиусов превышают предыдущие на одинаковую величину. Чем ближе расположены точки, тем точнее будет построен график гиперболы.
Как построить график гиперболы по уравнению
Каноническое уравнение гиперболы записывают таким образом:
где \(«a»\) и \(«b»\) являются положительными действительными числами, причем, \(«а»\) может быть больше или меньше, чем \(«b»\).
Важно отметить, что гипербола обладает двумя симметричными ветвями и двумя асимптотами.
Построение гиперболы можно рассмотреть на примере. Предположим, что она задана следующим уравнением:
Рассматриваемое уравнение необходимо привести к каноническому виду:
Так как в правой части требуется получить единицу, необходимо обе части начального уравнения поделить на 20:
Далее следует сократить обе дроби:
Затем нужно выделить квадраты в знаменателях:
В результате получено каноническое уравнение:
Существует два подхода к построению гиперболы:
- геометрический;
- алгебраический.
С практической точки зрения, эффективнее воспользоваться расчетами. В первую очередь следует определить асимптоты:
Асимптоты равны:
На втором этапе можно определить вершины гиперболы, которые соответствуют точкам на оси абсцисс с координатами:
При у=0, каноническое уравнение гиперболы примет вид:
Таким образом:
Вершины гиперболы:
Затем необходимо определить дополнительные точки. В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Согласно каноническому уравнению, можно выразить:
В результате получим две функции. Первая функция определяет верхние дуги гиперболы:
Вторая функция выражает нижние дуги гиперболы:
Напрашивается нахождение точек с абсциссами:
На последнем этапе следует изобразить асимптоты, вершины, дополнительные точки, симметричные точки в других координатных четвертях:
После того, как все точки соединены, будет изображена гипербола.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так