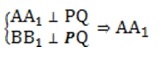Перпендикулярные прямые

Какие прямые называются перпендикулярными

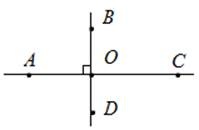
Схематично перпендикулярные линии АС и ВD будут выглядеть таким образом:

Обозначение перпендикулярных прямых в геометрии имеет такой вид:

\(AC\perp BD\)

Признак перпендикулярности, какие условия необходимы, чему равен угол

Угол между парой пересекающихся линий в пространстве может быть прямым. В таком случае рассматриваемые прямые будут перпендикулярными.

Если угол, который образовали две скрещивающиеся прямые, будет прямым, то такие линии также будут перпендикулярными. Исходя из данного утверждения, можно заключить, что перпендикуляры на плоскости являются пересекающимися, а перпендикулярные линии в пространстве могут быть пересекающимися и скрещивающимися. Таким образом, выражения «прямые а и b перпендикулярны» и «прямые b и а перпендикулярны» можно считать равноправными. Согласно этому определению, сформулировано понятие взаимно перпендикулярных прямых.

При определении перпендикулярности линий необходимо учитывать их характеристики, которые имеют большое значение в решении задач. Основные признаки:

1. Через какую-то точку А возможно начертить единственную перпендикулярную линию основному отрезку, остальные линии будут являться наклонными и могут скрещиваться.
2. Несколько перпендикуляров ни при каких условиях не будут между собой пересекаться.

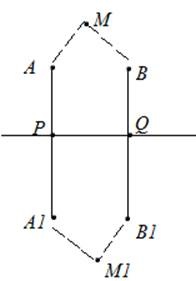
К примеру, можно изобразить на рисунке прямую PQ и пару линий, которые перпендикулярны ей: АА и ВВ. Необходимо доказать, что заданные прямые не имеют точек пересечения.

Подтверждение целесообразно строить с помощью метода «от обратного». Предположив, что прямые будут пересекаться в точке М1, получим какую-то точку М в другой полуплоскости, относительно прямой PQ. Таким образом, две точки пересекают две прямые, что не соответствует аксиоме. Поэтому предположение является неверным, а линии АА и ВВ не имеют точек пересечения:

Можно сделать вывод о том, что пара прямых, перпендикулярных третьей, не обладают общими точками пересечения.                          

Теорема о перпендикулярных прямых, как доказать

Задачи на перпендикулярные прямые, как правило, решают с учетом свойств этих линий. Доказательством перпендикулярности прямых является прямой угол, который они составляют. В том случае, когда требуется определить их перпендикулярность при известных уравнениях прямоугольной системы координат, следует применить необходимое и достаточное условие перпендикулярности линий.

Теорема 1

Подтверждением  данной теоремы является определение направляющего вектора прямой и перпендикулярности линий.

Допустим, что имеется прямоугольная декартовая система координат Оху, на которой заданы уравнения для прямой на плоскости, определяющие линии а и b. Направляющие векторы, характерные для данных прямых а и b, можно обозначить, как:

\(\vec{a}\) и \(\vec{b}\)

Согласно формуле прямых а и b, необходимым и достаточным условием является перпендикулярность векторов \(\vec{a}\) и \(\vec{b}.\)

Данное утверждение справедливо в том случае, когда скалярное произведение векторов:

\(\vec{a}=(a_{x};a_{y})\) и \(\vec{b}=(b_{x};b_{y})\) не равно нулю, а запись обладает таким видом:

\((\vec{a};\vec{b})=a_{x}*b_{x}+a_{y}*b_{y}=0\)

Таким образом, необходимое и достаточное условие перпендикулярности линий а и b, которые расположены в прямоугольной системе координат Оху на плоскости, представляет собой следующее выражение:

\((\vec{a};\vec{b})=a_{x}*b_{x}+a_{y}*b_{y}=0\)

где \(\vec{a}=(a_{x};a_{y})\) и \(\vec{b}=(b_{x};b_{y})\) являются направляющими векторами линий а и b.

Данную теорему целесообразно использовать в том случае, когда требуется определить координаты направляющих векторов, либо, когда известны канонические или параметрические уравнения прямых на плоскости заданных линий а и b.

В данном отношении запись будет иметь такой вид:

\((\vec{a};\vec{b})=a_{x}*b_{x}+a_{y}*b_{y}+ a_{z}*b_{z}=0\)

где \(\vec{a}=(a_{x};a_{y})\)

\(\vec{b}=(b_{x};b_{y})\)

\(\vec{z}=(z_{x};z_{y})\)

являются направляющими векторами прямых а и b.

Теорема 2

Доказательство этой теоремы заключается в применении рассматриваемого условия в том случае, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. Таким образом, имея общее уравнение прямой вида:\( A_{x}+B_{y}+C=0\)

а также уравнение прямой в отрезках вида:

\(\frac{x}{a}+\frac{y}{b}=1\)

и уравнение прямой с угловым коэффициентом вида y = kx + b, координаты векторов можно определить.

В том случае, когда линия а на плоскости определена с помощью уравнения с угловым коэффициентом:

\(y=k_{1}x+b_{1}\)

и прямая b имеет вид:

\(y=k_{2}x+b_{2}\)

тогда координаты нормальных векторов будут следующие:

\((k_{1};-1)\) и \((k_{2};-1)\)

Условие перпендикулярности соответствует выражению:

\(k_{1}*k_{2}+(-1)*(-1)=0\Leftrightarrow k_{1}*k_{2}=-1\)

Теорема 3

Данное условие действует при наличии возможности определения направляющего вектора одной прямой и координат нормального вектора другой. Одна прямая должна быть задана каноническим или параметрическим уравнением, а другая представлена в виде общего уравнения прямой, уравнением в отрезках или уравнением с угловым коэффициентом.