Как построить график линейной функции
Что такое линейная функция
В математической науке установленные и предполагаемые связи между теми или иными величинами принято обозначить функциональными зависимостями. В качестве примера можно рассмотреть объем денежных средств, который является функцией заработной платы сотрудника. Вес представляет собой функцию от потребляемого количества пищи. Расстояние считают функцией времени, то есть при увеличении времени в пути растет число пройденных метров. При рассмотрении данной темы в математике нередко можно встретить понятие «линейная функция». Представим определение этого термина.
Линейной называют функцию, записанную в следующем виде: y=kx+b
Сформулированное понятие применимо к функциональным зависимостям с единственной переменной. Таким образом, функция представляет собой правило, согласно которому одному из элементов некоторого множества, то есть аргументу, ставится в соответствие определенный компонент в единственном числе, принадлежащий другому множеству. В процессе рассмотрения функции y=f(x) допустимо записать для каждого приемлемого значения, которое принимает переменная x в виде аргумента, соответствующее одно значение переменной у, являющейся функцией.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Ограничение для линейной функции в виде области определения имеет большое значение. В определенных ситуациях для функциональных зависимостей подходят только те аргументы, которые удовлетворяют некоторым условиям. К примеру, если х стоит в выражении под знаком квадратного корня, то для переменной следует исключить значения с отрицательным знаком.
В том случае, когда линейная функция записана в формате y=kx+b, коэффициенты k и b представляют собой любые числовые значения. Таким образом, под линейной функцией понимают взаимосвязь, выраженную прямо пропорциональным отношением функции и аргумента. Выбор наименования линейной функциональной зависимости обусловлен ее графическим изображением в виде прямой линии.
При рассмотрении какой-либо функции оперируют понятиями ее области определения D(y) и области значений E(y). Руководствуясь изученным теоретическим материалом по теме, допустимо сделать вывод о том, что в случае линейной функции y=kx+b аргумент принимает любые значения. Таким образом, областью определения рассматриваемой функциональной зависимости является множество действительных чисел D(y)=R, то есть \(D(y)=(−\infty;+\infty)\).
С другой стороны, функция и ее аргумент прямо пропорционально взаимосвязаны. В результате описанной зависимости во время увеличения аргумента х возрастает значение функции у. Допустимо предположить справедливость равенства у любым значениям по аналогии с х, то есть E(y)=R. У данного утверждения существуют некоторые ограничения. Озвученные условия обусловлены тем, что в соотношении y=kx+b при нулевом значении коэффициента k и любом значении коэффициента b функция обладает одинаковыми величинами, независимо от х. Озвученные рассуждения можно представить с помощью математической записи:
\(y = kx + b:{\rm{ }}\left[ \begin{array}{l}E\left( y \right) = \mathbb{R}{\rm{ при }}k \ne 0\\E\left( y \right) = \left\{ b \right\}{\rm{ при }}k = 0.\end{array} \right.\)
Свойства
В процессе решения заданий на линейные функции полезно использовать общепринятые правила, чтобы упростить вычисления и исключить ошибки. С помощью таких закономерностей допустимо выражать величины с помощью известных значений компонентов функциональных зависимостей, рассчитывать переменные, формулировать порядок действий при построении графических изображений. Главным свойством множества линейных функций считают пропорциональность приращения функции и увеличения ее аргумента. Подобная закономерность обобщает прямую пропорциональность в математике и других науках. Перечислим полезные свойства линейных функций:
- величина k, обозначающая угловой коэффициент прямой, равна тангенсу угла \(\alpha \in \left[0;{\frac {\pi }{2}}\right)\cup \left({\frac {\pi }{2}};\pi \right)\), образованному прямой линией и положительным направлением оси абсцисс, и рассчитывается путем следующих вычислений: \(k=\mathrm {tg} \,\alpha ={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}={\frac {y_{1}-y_{2}}{x_{1}-x_{2}}}\);
- при выполнении условия, когда коэффициент k обладает строго положительным значением, то есть k>0, прямая линия составляет острый угол с положительным направлением оси абсцисс;
- в том случае, когда коэффициент k принимает строго отрицательное значение, то есть k<0, между прямой линией и положительным направлением оси абсцисс образуется тупой угол;
- если коэффициент k характеризуется нулевым значением, то есть k=0, то графическое изображение функции в виде прямой и ось абсцисс расположены параллельно относительно друг друга;
- пара прямых, выраженных с помощью \(y=k_{1}x+b_{1} и y=k_{2}x+b_{2}\), образуют угол на координатной плоскости, который рассчитывается с помощью формулы \(\mathrm {tg} \,\alpha =\left|{\frac {k_{1}-k_{2}}{1+k_{1}k_{2}}}\right|, где k_{1}k_{2}\neq -1\), где \(k_{1}k_{2}\neq -1\), то есть прямые линии нельзя назвать взаимно перпендикулярными, при \(k_{1}=k_{2} ~\alpha =0\), и прямые расположены на графике параллельно;
- величина b представляет собой параметр ординаты точки, в которой прямая пересекается с осью ординат;
- в том случае, когда b=0, прямая обладает общей точкой пересечения с началом координат на плоскости;
- линейная функция характеризуется монотонностью и не является выпуклой при рассмотрении на всей области определения \((\mathbb {R} )\);
- производная f'(x) и первообразная F(x) функции f(x)=kx+b вычисляются с помощью формул \(f'(x)=k, F(x)={\frac {kx^{2}}{2}}+bx+C\);
- функцию, которая является обратной относительно функциональной зависимости f(x), рассчитывают с помощью соотношения \(f^{-1}(x)={\frac {1}{k}}\,x-{\frac {b}{k}}\).
Как построить
Графическое решение задач в алгебре, физике, геометрии и других областях научных знаний позволяет наглядно представить зависимость между теми или иными величинами, выявить связи между параметрами каких-либо процессов или явлений. В частности, линейная функция, являющаяся вещественной, с единственной вещественной переменной на координатной плоскости имеет вид прямой линии. С целью построения графика такой функциональной зависимости y=kx+b удобно воспользоваться стандартным алгоритмом действий:
- в начале построения на оси ординат Y (Х=0) обнаружить точку, характеризующуюся равенством y=b,;
- двигаясь по графику в правую сторону относительно оси абсцисс Х и совершая k шагов вверх (или вниз, в зависимости от знака k), следует отметить точку графика;
- предыдущий этап необходимо повторить в случае необходимости более точного построения графического изображения рассматриваемой функциональной зависимости;
- в результате последующего соединения построенных точек формируется прямая линия, которая представляет собой график изучаемой линейной функции.
Формула
Рассмотрим, чему равна линейная функция n при условии, что переменные соответствуют следующим значениям:
\(x=(x_{1},x_{2},\dots ,x_{n})\)
В таком случае справедливым является следующее соотношение:
\(f(x)=a_{0}+a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}\)
Тогда \(a_{0},a_{1},a_{2},\dots ,a_{n}\) обозначают фиксированные числовые значения. В качестве области, на которой определяется рассматриваемая линейная функциональная зависимость, подразумевают n-мерное пространство переменных \(x_{1},x_{2},\dots ,x_{n}\) из множества вещественных или комплексных чисел.
Если предположить, что \(a_{0} \) обладает нулевым значением, то в таком случае линейная функция приобретает свойство однородности, то есть становится линейной формой. При выполнении условия, когда используемые в записи функциональной зависимости переменные \(x_{1},x_{2},\dots ,x_{n}\) и коэффициенты \(a_{0},a_{1},a_{2},\dots ,a_{n}\) принадлежат к множеству вещественных чисел, линейная функция характеризуется определенным графическим изображением. В (n+1)-мерном пространстве переменных \(x_{1},x_{2},\dots ,x_{n}\),y такой график представляет собой n-мерную гиперплоскость \(y=a_{0}+a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}\). Частным случаем служит прямая линия на координатной плоскости при условии, что n=1.
График
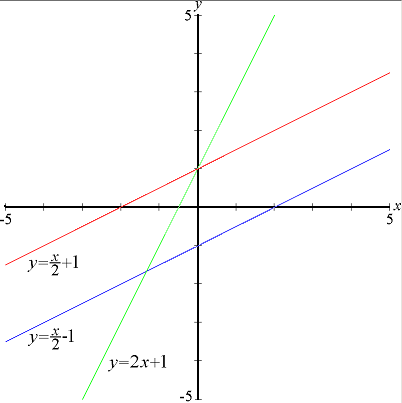
Примеры графического изображения линейной функции на плоскости с координатными осями:
Источник: ru.wikipedia.org
Примеры решения задач
Задано несколько линейных функций:
y=-2x+4;
y=2x-4;
y=2x+4.
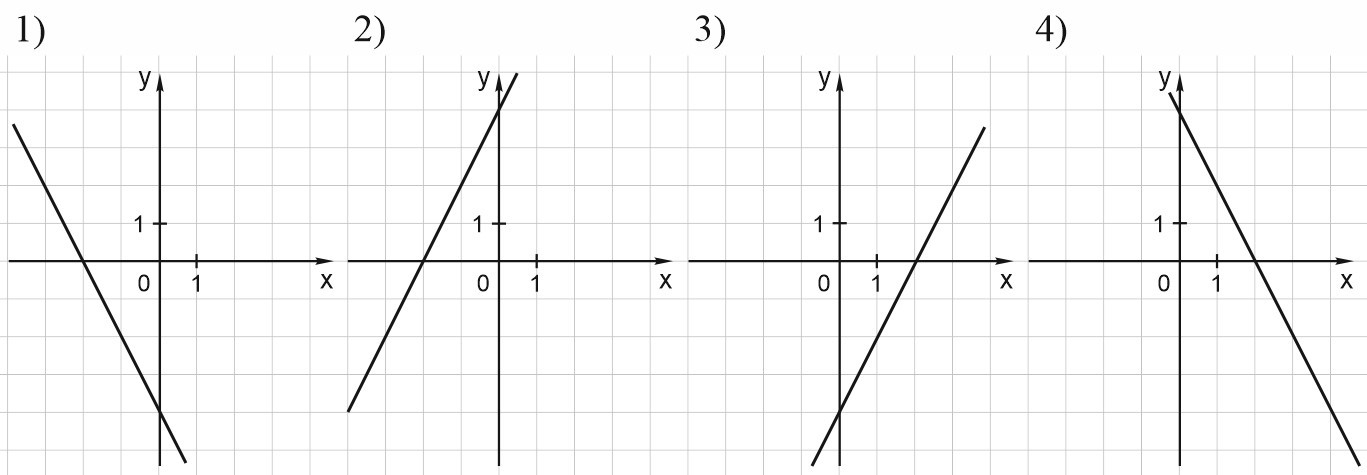
Необходимо выявить, в чем заключается соответствие между представленными функциональными зависимостями и их графическими изображениями.
Источник: ege-study.ru
Решение
Поиск ответа на задачу следует начать с рассмотрения первой по порядку функции:
y=-2x+4
Заметим, что данная функциональная зависимость представлена в стандартном формате. Таким образом, целесообразно воспользоваться свойствами для коэффициента функции, изученными в теоретическом разделе. Проанализируем значение коэффициента:
k=-2 < 0
Так как коэффициент принимает отрицательное значение, допустимо сделать вывод об убывании исследуемой функции. Далее заметим, что b=4. При этом точка, в которой пересекаются прямая и ось ординат, расположена выше, чем нулевая отметка на графике. Удовлетворяет озвученным условиям построения графика функциональной зависимости изображение под номером 4.
Перейдем к следующей формуле:
y=2x-4.
Аналогично предыдущему примеру рассмотрим в первую очередь коэффициент:
k=2 > 0
Исходя из того, что значение коэффициента больше нуля, допустимо сделать вывод о возрастании функции на графике. Одновременно с этим условием b=-4. Тогда общая точка для прямой линии и оси ординат будет отмечена ниже относительно нуля. Таким образом, описание графического изображения рассматриваемой функции совпадает с примером на рисунке 3.
Завершим решение задания определением графика для функциональной зависимости, выраженной уравнением:
y=2x+4
Значение коэффициента со знаком плюса, то есть k=2 > 0, свидетельствует о возрастании функции в рамках координатной плоскости. Вместе с тем, b=4. Таким образом, точка, в которой пересекаются прямая линия и ось Оу, расположена выше, чем нулевая отметка. Данное описание соответствует графическому изображению на 2 рисунке.
Ответ: графики под номерами 4, 3, 2.
Требуется подобрать для заданных линейных функций соответствующие графические изображения:
y=2x;
y=-2x;
y=x+2;
y=2.
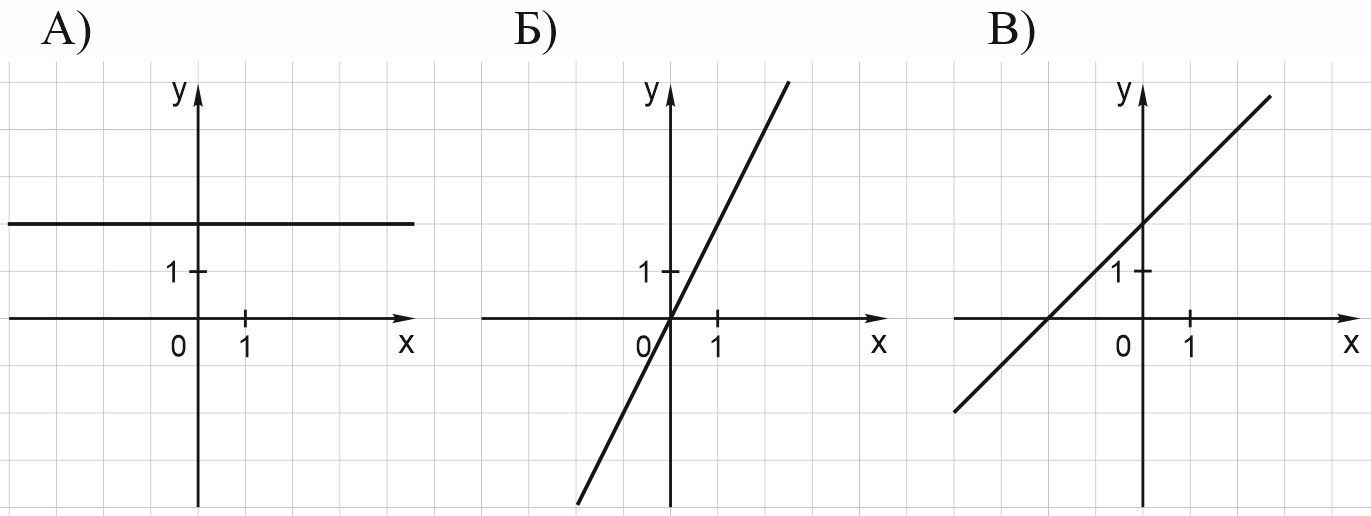
Источник: ege-study.ru
Решение
По аналогии с первой задачей воспользуемся стандартным алгоритмом исследования функциональных зависимостей. Целесообразно обратиться к перечисленным ранее свойствам линейных функций. В результате в зависимости от значений, которые принимают коэффициенты, записанные в формулах по условию, допустимо выявить особенности размещения графических изображений функций на координатной плоскости. По итогам анализа остается сопоставить полученные сведения с представленными в задании графиками.
Начнем с первого изображения. Здесь прямая линия расположена параллельно оси абсцисс и пересекает отметку с координатами (0;2). Таким образом, первый график соответствует выражению для функциональной зависимости под номером 4, то есть:
у=2.
Следующая прямая линия пересекает точку начала координат. Под озвученные условия подходит пара вариантов, то есть первая и вторая формула. Заметим, что рассматриваемая функция характеризуется свойством возрастания. Таким образом, второму рисунку соответствует математическое соотношение, записанное под номером 1:
у=2х.
На графике под номером 3 изображена возрастающая функция. При таком поведении на координатной плоскости точка, в которой пересекаются прямая линия и ось ординат, расположены выше, чем нулевая отметка. Из записанного рассуждения можно сделать вывод о том, что изучаемому графическому изображению соответствует третий вариант формулы, а именно:
y=x+2.
Ответ: изображенные в условии задания графики соответствуют функциям под номерами 4, 1, 3.
Нужно вычислить значения, которые принимают координаты точки пересечения графических изображений следующих функциональных зависимостей:
\(y_1=2x-5\);
\(y_2=x+3\).
Решение
Исходя из особенностей условия, задачу допустимо решать двумя способами. В первом случае можно выполнить построение графических изображений представленных функциональных зависимостей с последующим поиском координат точки, в которой прямые линии пересекаются. По озвученному алгоритму реализован графический метод решения. С целью тренировки практических навыков применим в данном примере аналитический метод поиска ответа, который состоит в решении уравнений.
Заметим, что общая точка для рассматриваемых функций расположена одновременно на прямых линиях, которые являются их графиками. Таким образом, координаты этой отметки допустимо применить для первой и второй функциональной зависимости путем подстановки. В результате будут сформированы справедливые равенства. В процессе вычисления абсциссы точки пересечения графических изображений необходимо записать правые части уравнений через знак равенства:
2x-5=x+3
На следующем этапе рассчитаем ответ к полученному линейному уравнению:
2x-x=3+5
х=8
Выполним повторно подстановку рассчитанного значения переменной в математическое выражение для какой-либо исходной функции. Получим следующее соотношение:
\(y=2\cdot 8-5=16-5=11\)
Ответ: (8;11).
Требуется определить координаты точек, в которых пересекается графическое изображение линейной функции y=0,5x+3 и координатные оси на плоскости.
Решение
На первом этапе рассмотрим алгоритм действий для поиска отметки, являющейся общей для графика функциональной зависимости из условия задания и оси абсцисс:
y=0
0,5x+3=0
0,5x=-3
\(x=-3 \div 0,5\)
x=-6.
Таким образом, искомая точка расположена на плоскости в отметке с координатами (-6;0). Затем перейдем к вычислению координат точки, в которой пересекаются графическое изображение заданной функции и ось ординат:
x=0
\(y=0,5\cdot 0+3=3\)
Общая точка графика функциональной зависимости и оси Oy соответствует координатам (0;3).
Ответ: (-6;0), (0;3).
Необходимо выяснить, принадлежат ли точки с координатами (3;-13) и (-5;-4) графику линейной функциональной зависимости, выраженной формулой: y=-4x-1.
Решение
Поочередно выполним подстановку координат каждой из представленных в условии задания отметок в математическое соотношение, выражающее линейную функцию. На следующем шаге проверим справедливость полученных уравнений.
x=3, y=-13
\(-13=-4\cdot 3-1\)
-13=-13
Сформулированная запись справедлива. Из данного утверждения можно сделать вывод о принадлежности рассматриваемой точки исходной прямой. Таким образом, первая отметка расположена на графическом изображении функции.
x=-5, y=-4
\(-4=-4\cdot (-5)-1\)
-4=19
Полученное равенство является неверным. Исходя из этого, прямая через вторую точку не проходит.
Ответ: график линейной функции проходит только через первую точку, имеющую координаты (3;-13).
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так