Решение линейных уравнений с двумя переменными

Понятие линейного уравнения с двумя переменными

Определение 1

Определение 2

Как выглядит график, особенности построения

В качестве эффективного метода решения линейного уравнения можно изобразить график в виде прямой линии, точки которой будут лежать в координатной плоскости xOy. Пусть дано линейное уравнение:

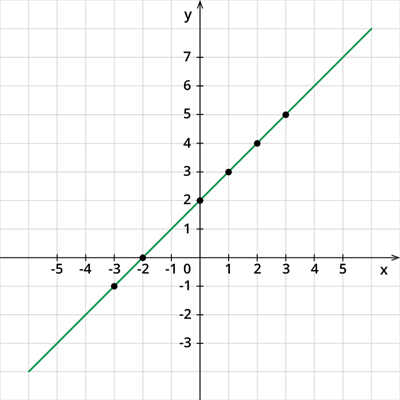
−x+y−2=0

Достаточно просто подобрать несколько решений:

(3;5), (2;4), (1;3), (0;2), (−2;0)

Далее необходимо построить найденные точки в общей координатной плоскости, а также убедиться, что эти точки расположены на одной прямой t.

Прямая t представляет собой график уравнения, определяемого по формуле:

−x+y−2=0

Так же данная прямая t является геометрической моделью этого уравнения.

Можно сделать основной вывод: в том случае, когда пара чисел (x; y) удовлетворяет уравнению ax+by+c=0, точка М(x; y) расположена на прямой t. Обратная формулировка: при расположении точки М(x; y) на прямой t, пара чисел (x; y) удовлетворяет уравнению ax+by+c=0. График уравнения ax+by+c=0 представляет собой прямую при коэффициентах a и b, которые одновременно не равны.

Алгоритм, согласно которому можно построить график уравнения ax+by+c=0 при \(a\neq0\), \(b\neq0\), включает следующие пункты:

1. Выбрать какое-либо подходящее значение для переменной \(x=x_{1}\). Далее из уравнения \(ax_{1}+by+c=0\) найти значение \(y=y_{1}\).
2. Определить другое значение переменной \(x=x_{2}\). Затем из уравнения \(ax_{2}+by+c=0\) рассчитать значение \(y=y_{2}\).
3. На координатной плоскости xOy отметить точки: \((x_{1};y_{1});(x_{2};y_{2})\).
4. Через данные точки построить прямую, представляющую собой искомый график.

Примеры задач, как решать систему с двумя неизвестными

Решение

В первую очередь следует выполнить подстановку x=0 в уравнение:

0−2y−4=0

−2y=4

y=4:(−2)

y=−2

Далее необходимо подставить в уравнение y=0:

x−2⋅0−4=0

x−4=0

x=4

Точки (0;−2) и (4;0), полученные в результате расчетов, можно отметить на графике в прямоугольной системе координат. На следующем этапе требуется соединить полученные точки прямой линией. График примет следующий вид:

Ответ: построенная линия представляет собой график линейного уравнения x−2y−4=0.

Решение

В первую очередь необходимо выполнить подбор соответствующей пары чисел х и y. Предположим, что х = 0, в таком случае начальное уравнение примет вид уравнения с одной неизвестной:

0 + у – 3 = 0

у = 3

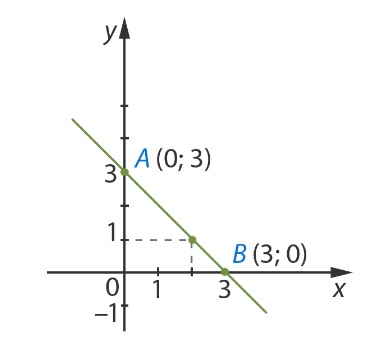
Таким образом, первая пара чисел, которая соответствует решению заданного уравнения (0; 3). В результате определена точка А(0; 3).

Предположим, что у = 0. Тогда заданное уравнение примет вид уравнения с одной переменной:

х + 0 – 3 = 0

Таким образом:

х = 3

В результате определена точка В(3; 0).

Затем можно отметить на графике полученные точки и провести через них прямую линию:

Ответ: любая точка на построенной на графике прямой является решением заданного уравнения.

Решение

Так как для построения графика достаточно знать две точки, найдем их и возьмем третью точку для контроля:

Можно выбрать х = 0 и найти у:

3 * 0 – 2у + 6 = 0

-2у = -6

у = 3

Далее возьмем для расчетов у = 0 и определим х:

3x – 2*0 + 6 = 0

3x + 6 = 0

3x = -6

х = -2

Для проверки подберем х = 2 и вычислим у:

3 * 2 – 2у + 6 = 0

-2у = -12

у = 6

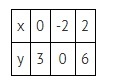
Пользуясь полученными данными, составим таблицу:

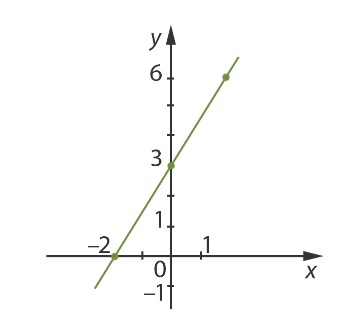
С ее помощью можно построить график:

Ответ: построенный график является решением данного уравнения.