Можно ли вписать окружность в параллелограмм и наоборот
Параллелограмм, вписанный в окружность
Параллелограмм — это четырехугольник с попарно параллельными и равными противолежащими сторонами.
Все четыре стороны этой фигуры принадлежат одной плоскости.
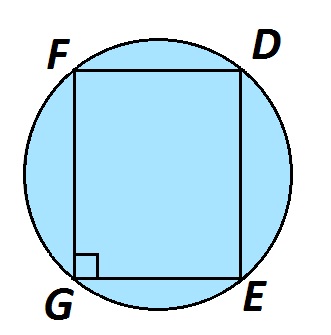
Четырехугольник можно вписать в окружность, если сумма его противоположных углов равна 180°. Если сумма противоположных углов параллелограмма равна 180°, то такой параллелограмм — прямоугольник.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
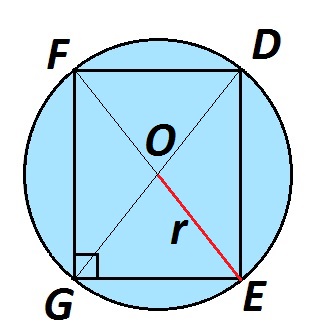
Точка пересечения диагоналей прямоугольника является центром описанной окружности.
Свойство радиуса окружности, описанной около прямоугольника
Радиус описанной окружности равен половине диагонали прямоугольника.
Пример решения задачи. Параллелограмм и описанная окружность
Дано: прямоугольник со сторонами 8 см и 6 см.
Найти: радиус описанной окружности.
Решение: диагональ прямоугольника равна \(\sqrt{8^2+6^2}=10 (см)\); следовательно, радиус описанной окружности равен 10÷2=5 (см).
Ответ: 5 см.
Параллелограмм, описанный около окружности
Когда параллелограмм можно описать около окружности? Другими словами — при каком условии можно вписать окружность или круг в параллелограмм?
Так как параллелограмм — это частный случай четырехугольника, будет действовать то же правило, что и для любого другого четырехугольника. Окружность можно вписать в параллелограмм, только если суммы его противоположных сторон равны.
Это условие выполняется только для тех параллелограммов, у которых все стороны равны, то есть только для ромба (и квадрата, как частного случая ромба).
Если в задаче дано, что в параллелограмм вписана окружность, то из этого условия можно сделать вывод, что все его стороны равны, и данный параллелограмм является ромбом. Если по условию один из углов этого параллелограмма прямой, то такой параллелограмм — квадрат.
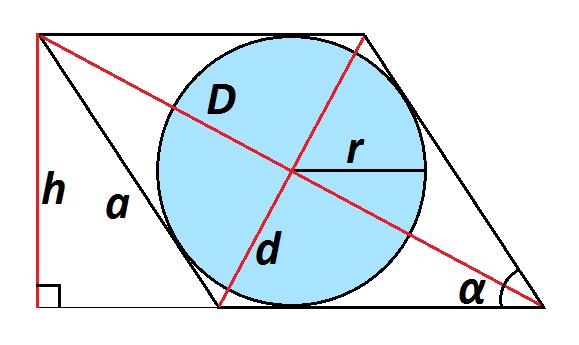
Радиус окружности, вписанной в ромб
Радиус вписанной в ромб окружности можно найти несколькими способами.
Если известны диагонали и сторона
\(r=\frac{Dd}{4a}\), где:
- r — радиус вписанной окружности;
- а — сторона ромба;
- D — большая диагональ;
- d — меньшая диагональ.
Если известны диагонали
\(r=\frac{Dd}{2\sqrt{D^2+d^2}}\), где:
- r — радиус вписанной окружности;
- D — большая диагональ;
- d — меньшая диагональ.
Если известны сторона и угол
\(r=\frac{a·\sin\alpha}2\), где:
- r — радиус вписанной окружности;
- а — сторона ромба;
- α — острый угол.
Если известны диагонали и угол
\(r=\frac d2\cos\alpha/2=\frac d{2\sqrt2}\sqrt{1+\cos\alpha}\)
\(r=\frac D2\sin\;\alpha/2=\frac D{2\sqrt2}\sqrt{1-\cos\alpha}\), где:
- r — радиус вписанной окружности;
- D — большая диагональ;
- d — меньшая диагональ;
- α — острый угол.
Если известны диагонали и сторона
\(r=\frac{D\sqrt{a^2-D^2/4}}{2a}\)
\(r=\frac{d\sqrt{a^2-d^2/4}}{2a}\), где:
- r — радиус вписанной окружности;
- D — большая диагональ;
- d — меньшая диагональ;
- а — сторона ромба.
Если известна высота ромба
\(r=\frac h2\), где:
- r — радиус вписанной окружности;
- h — высота ромба.
Если известны площадь и полупериметр
\(r=\frac Sp\), где:
- r — радиус вписанной окружности;
- S — площадь ромба;
- p — полупериметр ромба.
Задачи. Параллелограмм и вписанная окружность.
Дано: параллелограмм со вписанной окружностью. Одна из сторон параллелограмма равна 5 см.
Найти: периметр параллелограмма.
Решение: в параллелограмм можно вписать окружность только если это ромб. Четыре стороны ромба равны. Следовательно, периметр данного параллелограмма равен 5·4=20 (см).
Ответ: 20 см.
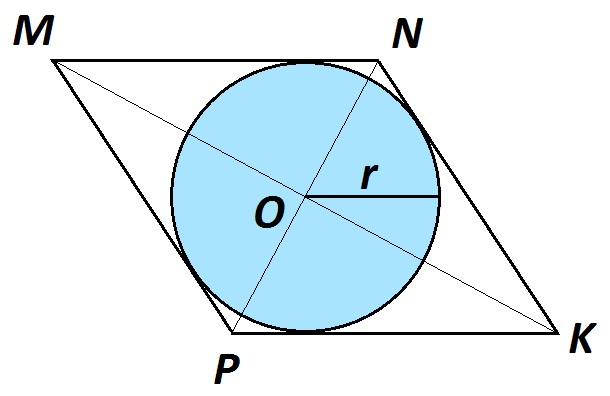
Дано: параллелограмм MNKP с диагоналями 12 см и 16 см. В MNKP вписана окружность.
Найти: радиус вписанной окружности.
Решение:
Из того, что в параллелограмм MNKP вписана окружность, делаем вывод, что MNKP — ромб.
Параллелограмм MNKP не является квадратом, так как его диагонали не равны. MK=16 см, NP=12 см.
ΔMOP прямоугольный, \(∠MOP=90°. MO=8 см, OP=6 см. S_{MОР}=(8·6)÷2=24 (см^2)\).
\(S_{MNKP}=24·4=96 (см^2)\).
По теореме Пифагора \( MP=\sqrt{MО^2+ОР^2}=\sqrt{8^2+6^2}=10 (см)\).
Полупериметр MNKP равен 20 см.
Следовательно, радиус вписанной окружности равен
\(r=\frac Sp=96÷10=9,6 (см)\).
Ответ: 9,6 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так