Метод координат
Что такое метод координат в алгебре и геометрии
Часто при решении задач в алгебре и геометрии используют метод координат.
Сущность метода заключается в том, что наиболее удобным способом задается система координат, затем находят координаты точек и определяют искомые величины с помощью уравнений.
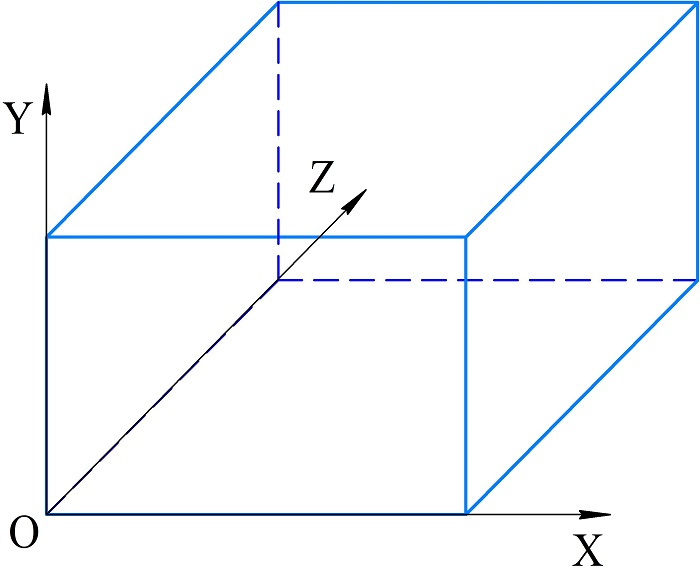
Например, начало системы координат располагают в какой-либо вершине фигуры, а координатные оси направляют вдоль ребер.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Приведем общий алгоритм решения задач с использованием метода координат:
- Задают систему координат (пространственную или на плоскости).
- Находят и записывают координаты опорных точек, например, координаты начала и конца отрезка, координаты точек на плоскости.
- Составляют необходимые уравнения: плоскости, прямой.
- Решают задачу с использованием формул.
Метод координат применяется для определения:
- расстояний между прямыми, плоскостями, прямой и плоскостью;
- углов между прямой и плоскостью, прямыми и плоскостями.
Основное преимущество рассматриваемого метода состоит в том, что для решения задач нет необходимости делать дополнительные построения. Достаточно задать и указать на чертеже оси координат.
Применение метода координат в пространстве
Положение объекта в пространстве однозначно задается тремя координатами. Поэтому при использовании метода координат в стереометрии задают трехмерную систему координат.
При решении задач в пространстве оперируют понятием вектора. В данном случае вектор по своей сути является отрезком. Координаты вектора находят как разницу координат начальной и конечной точек.
Выпишем уравнения применяемых пространственных объектов:
- Координаты вектора \(\overrightarrow{AB}\), где начальная точка — \(A\;(x_1,\;y_1,\;z_1)\), конечная — \(B\;(x_2,\;y_2,\;z_2)\): \(\overrightarrow{AB}\;(x_2-x_1;\;y_2-y_1;\;z_2-z_1)\).
- Уравнение плоскости: \(A\cdot x+B\cdot y+C\cdot z+D=0\).
- Каноническое уравнение прямой, проходящей через точку \(N\;(x_1,\;y_1,\;z_1): \frac{x-x_1}m=\frac{y-y_1}r=\frac{z-z_1}p\).
- Уравнение прямой в общем виде задается как линия пересечения двух плоскостей: \(\left\{\begin{array}{l}A_1x+B_1y+C_1z+D_1=0\\A_2x+B_2y+C_2z+D_2=0\end{array}\right.\)
- Нормальный вектор к плоскости, заданной уравнением \(A\cdot x+B\cdot y+C\cdot z+D=0:\overrightarrow n\;(A;\;B;\;C)\).
- Направляющий вектор прямой, заданной уравнением \(\frac{x-x_1}m=\frac{y-y_1}r=\frac{z-z_1}p: \overrightarrow s\;(m;\;r;\;p)\).
Нормальным вектором называется вектор, перпендикулярный к данной плоскости.
Направляющим вектором называют любой вектор, лежащий на данной прямой или параллельны ей. Координаты направляющего вектора не равны нулю.
Рассмотрим пример того, как составить уравнения прямой и плоскости по известным координатам точек.
Пусть имеются три точки \(A\;(x_1;\;y_1;\;z_1), B\;(x_2;\;y_2;\;z_2), C\;(x_3;\;y_3;\;z_3)\). Составить уравнение плоскости, проходящей через указанные точки, и уравнение прямой, проходящей через точки А, В.
Решение
Уравнение прямой \(АВ\) будет иметь вид: \(\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}\).
Уравнение плоскости в общем виде имеет вид: \(Ax+By+Cz+D=0\). Подставим известные координаты и запишем систему уравнений:
\(\left\{\begin{array}{l}A_1\cdot x_1+B_1\cdot y_1+C_1\cdot z_1+D=0\\A_1\cdot x_2+B_1\cdot y_2+C_1\cdot z_2+D=0\\A_1\cdot x_3+B_1\cdot y_3+C_1\cdot z_3+D=0\end{array}\right.\)
В системе три уравнения и четыре неизвестных. Поделим каждое уравнение на \(D\), получим:
\(\left\{\begin{array}{l}A\cdot x_1+B\cdot y_1+C\cdot z_1+1=0\\A\cdot x_2+B\cdot y_2+C\cdot z_2+1=0\\A\cdot x_3+B\cdot y_3+C\cdot z_3+1=0\end{array}\right.\)
Из полученной системы можно выразить коэффициенты \(A, B, C.\)
Применение метода координат на плоскости
Вариант применения метода координат на плоскости отличается лишь числом координат в уравнениях. Поскольку положение любого объекта на плоскости задается двумя координатами, уравнения также будут содержать две координаты — x и y.
При решении задач оперируют понятиями вектора и прямой.
Координаты вектора находят аналогично пространственным задачам.
Каноническое уравнение прямой на плоскости имеет вид: \(\frac{x-x_1}m=\frac{y-y_1}r\).
Примеры решения и формулы
Перейдем от теории к практике. Приведем основные формулы и рассмотрим конкретные примеры.
Формулы для вычисления углов
Косинус угла между прямыми равен косинусу угла между их направляющими векторами:
\(\cos\alpha=\frac{\overrightarrow{s_1}\cdot\overrightarrow{s_2}}{\left|\overrightarrow{s_1}\right|\cdot\left|\overrightarrow{s_2}\right|}=\frac{m_1\cdot m_2+r_1\cdot r_2+p_1\cdot p_2}{\sqrt{m_1^2+r_1^2+p_1^2}\cdot\sqrt{m_2^2+r_2^2+p_2^2}}\)
Синус угла между прямой и плоскостью равен синусу угла между направляющим вектором прямой и нормальным вектором плоскости:
\(\sin\alpha=\frac{\vert\overrightarrow s\cdot\overrightarrow n\vert}{\left|\overrightarrow s\right|\cdot\left|\overrightarrow n\right|}=\frac{\vert m\cdot A+r\cdot B+p\cdot C\vert}{\sqrt{m^2+r^2+p^2}\cdot\sqrt{A^2+B^2+C^2}}\)
Косинус угла между плоскостями равен косинусу угла между их нормалями:
\(\cos\alpha=\frac{\overrightarrow{n_1}\cdot\overrightarrow{n_2}}{\left|\overrightarrow{n_1}\right|\cdot\left|\overrightarrow{n_2}\right|}=\frac{A_1\cdot A_2+B_1\cdot B_2+C_1\cdot C_2}{\sqrt{A_1^2+B_1^2+C_1^2}\cdot\sqrt{A_2^2+B_2^2+C_2^2}}\)
Найти угол между прямой, заданной уравнением \(\frac{x-2}5=\frac{y-1}2=\frac z3\), и плоскостью, заданной уравнением \(-x+3y+4z=0\).
Решение
Угол между прямой и плоскостью равен углу между направляющим вектором прямой и нормалью плоскости. Направляющий вектор прямой — \(\overrightarrow s\;(5;\;2;\;3)\), нормаль к плоскости — \(\overrightarrow n\;(-1;\;3;\;4)\). Тогда синус угла между прямой и плоскостью вычисляется по формуле: \(\sin\alpha=\frac{\vert\overrightarrow s\cdot\overrightarrow n\vert}{\left|\overrightarrow s\right|\cdot\left|\overrightarrow n\right|}=\frac{\left|5\cdot(-1)+2\cdot3+3\cdot4\right|}{\sqrt{25+4+9}\cdot\sqrt{1+9+16}}=\frac{13}{\sqrt{988}}\).
Ответ: \(\sin\alpha=\frac{13}{\sqrt{988}}\).
Формулы расстояний
Расстояние от точки \(N\;(x_0;\;y_0;\;z_0)\) до плоскости определяют как длину перпендикуляра к плоскости, опущенного из заданной точки:
\(d=\left|\frac{Ax_0+By_0+Cz_0+D}{\sqrt{A^2+B^2+C^2}}\right|\)
Расстояние от точки \(N\;(x_0;\;y_0;\;z_0)\) до прямой, заданной уравнением \(Ax+By+C=0\):
\(d=\left|\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}\right|\)
Расстояние между скрещивающимися прямыми равно длине отрезка, проходящего через точку \(N\;(x_1,\;y_1,\;z_1)\), принадлежащую первой прямой, и точку \(M\;(x_2,\;y_2,\;z_2)\), принадлежащую второй прямой. Тогда расстояние между скрещивающимися прямыми вычисляется через смешанное произведение направляющих векторов \(\overrightarrow{s_1}\) и \(\overrightarrow{s_2}\) и вектора \(\overrightarrow{MN}\):
\(d=\frac{\left|(\overrightarrow{s_1}\times\overrightarrow{s_2})\cdot\overrightarrow{MN}\right|}{\left|\overrightarrow{s_1}\times\overrightarrow{s_2}\right|}\)
Решение смешанного произведения векторов не рассматривается в рамках школьного курса алгебры и геометрии.
Расстояние между двумя плоскостями можно также вычислить по расстоянию между скрещивающимися прямыми. Для этого на каждой из плоскостей задают прямую, затем вычисляют расстояние между прямыми, которое будет равно расстоянию между плоскостями.
Найти расстояние между плоскостью, заданной уравнением \(9x-y+5z-2=0\), и точкой \(M (-1; -2; -3)\).
Решение
Подставим известные координаты в формулу для вычисления расстояния от точки до плоскости, получим:
\(d=\frac{\left|9\cdot(-1)+(-1)\cdot(-2)+5\cdot(-3)+(-2)\right|}{\sqrt{81+1+25}}=\frac{\left|-24\right|}{\sqrt{107}}\approx2.3\).
Ответ: 2.3.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так