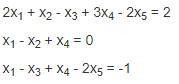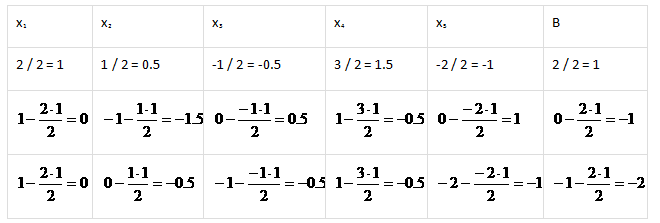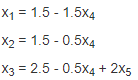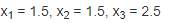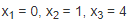Решение системы линейных уравнений методом Жордана-Гаусса

Метод Жордана Гаусса — история возникновения

Метод Жордана-Гаусса, то есть способ полного исключения неизвестных, применяют в алгебре для решения следующих задач:

• квадратные системы линейных алгебраических уравнений;
• поиск обратной матрицы;
• определение координат вектора в заданном базисе;
• поиск ранга матрицы.

Рассматриваемый метод представляет собой модифицированную теорию Гаусса. Методика получила название в честь К. Ф. Гаусса и немецкого геодезиста и математика Вильгельма Йордана.

Предпосылки для возникновения метода Гаусса появились еще до нашей эры. Объяснение этого способа можно найти в древней китайской книге под названием «Математика в девяти книгах». Труд был написан приблизительно в 150 году до нашей эры. Трактат является сборником разных задач по математике и способов их решений.

В Европе впервые начал изучать данный метод Исаак Ньютон. В процессе исследований древней литературы по математике ученый пришел к выводу о том, что отсутствует способ решения систем уравнений, которые предусматривают большое количество переменных.

Ньютон разработал схему решения в своем труде, который был представлен общественности в 1707 году. Данную методику активно использовали в разных пособиях и арифметических справочниках в течение последующих 100 лет.

Немецкий ученый К.Ф. Гаусс в 1810 году модернизировал способ Ньютона. Усовершенствованная методика была опубликована вместе с другими разработками исследователя. В результате метод преобразования в треугольную матрицу завоевал популярность и получил название в честь ученого.

Во второй половине ХІХ века ученый Жордан доработал способ Гаусса. Таким образом удалось получить способ приведения к диагональной матрице. Интересным фактом является точно такое же открытие другого ученого, однако название методики в настоящее время содержит имена Гаусса и Жордана.

Метод Жордана-Гаусса получил широкое распространение. Кроме поиска ответов к примерам по математике, данный способ необходим для решения инженерных задач, содержащих большое число неизвестных. В процессе решения систем уравнений, полученных из инженерно-технических задач, в первую очередь выбирают максимально большие по модулю переменные. Это позволяет минимизировать погрешность. Затем из матрицы по очереди убирают ненужные переменные.

Занимаясь расчетами инженерно-технических задач рассматриваемым способом, целесообразно использовать разные алгоритмы программирования. В результате полученные ответы характеризуются минимальной погрешностью.

Отличия рассматриваемого метода от метода Гаусса заключаются в том, что в последнем к нулям приводится только нижняя часть матрицы. Метода Жордана-Гаусса предполагает, что к нулям нужно привести также и верхнюю часть матрицы.

Обе методики позволяют определить базисное и общее решения системы уравнений. В случае базисного решения системы уравнений каждая свободная переменная обладает нулевым значением.  При общем решении системы уравнений основные переменные выражают через свободные переменные.

Практическое применение для решения систем линейных уравнений

Существует простой алгоритм действий для решения задач методом Жордана-Гаусса. Он состоит из следующих этапов:

1. Выбор первого с левой стороны столбца матрицы, содержащего, как минимум, одно отличное от нуля значение.
2. Когда самое верхнее число в данном столбце является нулем, следует заменить полностью первую строку матрицы на другую строку матрицы, в которой в аналогичном столбце отсутствует нуль.
3. Каждый элемент, находящийся в первой строке, необходимо поделить на верхний элемент выбранного столбца.
4. Из оставшихся строк требуется отнять первую строку, умноженную на первый элемент соответствующей строки для получения первым элементом каждой строки (за исключением первой) нуля.
5. Аналогичные действия предусмотрены для матрицы, которая получена из начальной матрицы путем удаления первой строки и первого столбца.
6. Процедуру повторяют n-1 раз. В результате получается верхняя треугольная матрица.
7. С целью оставить в предпоследней строке лишь 1 на главной диагонали, нужно отнять из предпоследней строки последнюю строку, которую умножили на соответствующий коэффициент.
8. В случае последующих строк предыдущий шаг повторяют. Таким образом, формируется единичная матрица и решение на месте свободного вектора (для него предусмотрены аналогичные преобразования).

Расширенный алгоритм действий, позволяющий найти обратную матрицу, целесообразно рассмотреть на примере решения задачи. Предположим, что:

\(A=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix} \quad a_{ii} \ne 0 \quad I=\begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix}\)

Прямой ход (алгоритм образования нулей под главной диагональю) предполагает в первую очередь деление первой строки матрицы А на \(a_{11},\) что даст в результате:

\({a_{11}}\) \(a_{1j}^1 \)\(= \frac{a_{1j} }{a_{11} },\)

j — столбец матрицы А.

Далее необходимо повторить действия для матрицы I. Запишем формулу:

\(b_{1s}^1 = \frac{b_{1s} }{a_{11} }\),

s — столбец матрицы I.

Таким образом:

\(A=\begin{pmatrix} 1 & a_{12}^1 & \cdots & a_{1n}^1 \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix} \qquad I=\begin{pmatrix} b_{11}^1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix}\)

Для того чтобы нуль образовался в первом столбце, потребуется:

\({\displaystyle a_{2j}^{1}=a_{2j}-a_{1j}^{1}a_{21}\ ,\dots ,\ a_{nj}^{1}=a_{nj}-a_{1j}^{1}a_{n1}}\)

В случае матрицы І следует повторить действия по формулам:

\({\displaystyle b_{2s}^{1}=b_{2s}-b_{1s}^{1}a_{21}\ ,\dots ,\ b_{ns}^{1}=b_{ns}-b_{1s}^{1}a_{n1}}\)

В результате:

\({\displaystyle A={\begin{pmatrix}1&a_{12}^{1}&\cdots &a_{1n}^{1}\\0&a_{22}^{1}&\cdots &a_{2n}^{1}\\\vdots &\vdots &\ddots &\vdots \\0&a_{n2}^{1}&\cdots &a_{nn}^{1}\end{pmatrix}}\qquad I={\begin{pmatrix}b_{11}^{1}&0&\cdots &0\\b_{21}^{1}&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\b_{n1}^{1}&0&\cdots &1\end{pmatrix}}}\)

Можно записать уравнения:

\(a_{ij}^k=\frac{a_{ij}^k}{a_{ii} } \qquad a_{ij}^k=a_{ij}^{k-1}-a_{kj}^k a_{ik}^{k-1}\)

С их помощью необходимо повторить действия, учитывая условия:

\(k = 1 \rightarrow n,i = k + 1 \rightarrow n,j = 1 \rightarrow n\)

Повтор операций для матрицы І по формулам:

\(b_{ik}^k=\frac{b_{ik}^k}{a_{ii} } \qquad b_{is}^k=b_{is}^{k-1}-b_{ks}^k a_{ik}^{k-1}\)

Следует принять во внимание, что:

\(k=1 \to n,\; i=k+1 \to n,\; s=1 \to n\)

В результате:

\({\displaystyle A={\begin{pmatrix}1&a_{12}^{1}&\cdots &a_{1n}^{1}\\0&1&\cdots &a_{2n}^{2}\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{pmatrix}}\qquad I={\begin{pmatrix}b_{11}^{1}&0&\cdots &0\\b_{21}^{2}&b_{22}^{2}&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\b_{n1}^{n}&b_{n2}^{n}&\cdots &b_{nn}^{n}\end{pmatrix}}}\)

Если использовать обратный ход, то есть алгоритм образования нулей над главной диагональю, в первую очередь нужно воспользоваться формулой:

\(a_{ij}^{k-1}=a_{ij}^{k-1}-a_{ij}^k a_{ik}^i,\)

В данном случае необходимо учитывать, что:

\(k=n \to 1,\; i=1 \to k-1,\; j=1 \to n\)

Затем требуется повторить действия для матрицы І, по формуле:

\(b_{is}^{k-1}=b_{is}^{k-1}-b_{is}^k a_{ik}^i\)

Выполняется условие:

\(k=n \to 1,\; i=1 \to k-1,\; s=1 \to n\)

В итоге получим, что:

\(A=\begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix} \qquad I=A^{-1}\)

Произвольный способ выбора разрешающих элементов

Особенность данного способа решения состоит в том, что столбы матрицы системы перебираются в определенной последовательности. В каждой колонке необходимо выбрать какой-то элемент с нулевым значением. Данный элемент называют разрешающим. Предположим, что в текущем столбце разрешающим элементом является:

\( \displaystyle{a_{ij}}.\)

Когда \(\displaystyle{a_{ij}\neq{1}}\), умножив строку \(\displaystyle{r_i} на \displaystyle{\frac{1}{a_{ij}}}\), требуется привести разрешающий элемент к значению 1. На следующем этапе предполагаются действия со строками. Это позволит обнулить каждый ненулевой элемент j-го столбца, за исключением разрешающего элемента.

Далее следует перейти к следующему столбцу. В процессе из каждой строки можно позаимствовать разрешающий элемент лишь единожды. Строки, которые являются нулевыми, исключаются по мере их возникновения. В том случае, когда разрешающий элемент станет невозможно выбрать, алгоритм прекращается.

Можно подробно рассмотреть этот способ. Сначала работать необходимо в первой колонке матрицы системы. Здесь требуется выбрать произвольный ненулевой элемент \(\displaystyle{a_{i1}\neq{0}}\), который является разрешающим. Если \(\displaystyle{a_{i1}\neq{1}}\), то следует умножить строку  \(\displaystyle{r_i} \) с разрешающим элементом на \(\displaystyle{\frac{1}{a_{i1}}}\).

В результате разрешающий элемент станет равен 1. При  \(\displaystyle{a_{i1}=1}\) не требуется выполнять умножение. Используя строку  \(\displaystyle{r_i}\), нужно обнулить другие ненулевые элементы первого столбца. Из строки  \(\displaystyle{r_i} \) выбирать разрешающие элементы в последующих шагах запрещено. Допустимо из некой строки выбирать разрешающий элемент только один раз.

На втором шаге нужно перейти к следующей колонке матрицы системы. Необходимо проверить наличие или отсутствие в этом столбце ненулевого элемента, который не принадлежит строке, имеющей разрешающий элемент, выбранный на предыдущем шаге.

Когда такой разрешающий элемент во втором столбце отсутствует, можно переходить к третьей, четвертой колонке и так далее. Переход следует закончить после нахождения столбца с нужным элементом, либо при отсутствии искомого столбца в матрице системы. В результате алгоритм будет завершен.

Предположим, что искомый столбец найден, и в нем присутствует разрешенный элемент.  Данный элемент нужно обозначить \(\displaystyle{b_{nk}}\). Далее по аналогии с первым шагом, если \(\displaystyle{b_{nk}\neq{1}}\), необходимо умножить строку \(\displaystyle{r_n}\) с разрешающим элементом на \(\displaystyle{\frac{1}{b_{nk}}}\). Затем следует обнулить другие ненулевые элементы k-го столбца.

Запрещено выбирать разрешающие элементы из строк, в которых были обнаружены разрешающие элементы на первом и втором этапе алгоритма. Когда обнуление завершено, можно переходить к следующему столбцу и так далее. Как только выбор разрешающего элемента станет невозможен, алгоритм закончится.

Выбор разрешающих элементов на главной диагонали матрицы системы

Данный способ предполагает использование метода прямоугольника. Результатом является диагональная матрица, то есть квадратная матрица с элементами, расположенными вне главной диагонали и равными нулю.

В качестве примера можно рассмотреть решение системы линейных уравнений:

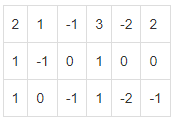
 Данную систему можно представить в виде матрицы:

 Векторы-столбцы базисного решения являются единичными векторами, которые образуют базис, а соответствующие им переменные называются базисными. Для получения единичных векторов применяют метод Жордана-Гаусса. Опорным решением называют базисное неотрицательное решение. Базисное решение системы линейных уравнений возможно в том случае, когда свободные переменные \((m>n)\) принимают нулевые значения.

Предположим, что имеется система линейных уравнений. Необходимо определить три базисных решения с помощью метода Жордана-Гаусса, а также назвать, какие из них являются опорными.

Система имеет вид:

 В определенной последовательности необходимо выбирать разрешающий элемент, расположенный на главной диагонали матрицы. Разрешающий элемент равен (2).
На его месте получаем 1, а в самом столбце следует записать нули. Другие элементы матрицы, в том числе, элементы столбца B, вычисляются, согласно правилу прямоугольника.

В процессе нужно выбрать четыре числа, которые расположены в вершинах прямоугольника и в любом случае содержат разрешающий элемент.

\(НЭ = СЭ - (А*В)/РЭ\)

\(РЭ \)— разрешающий элемент (2);

А и В — элементы матрицы, которые формируют прямоугольник с элементами СТЭ и РЭ.

Записать расчеты для каждого элемента можно в виде таблицы:

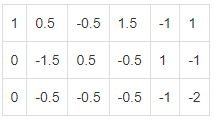
 Таблицу допустимо представить в таком виде:

 Разрешающий элемент равен (-1.5). Можно записать расчет каждого элемента в виде таблицы:

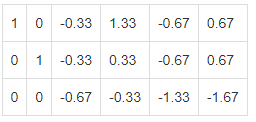
 Разрешающий элемент равен (-0.67). По результатам пересчета общее решение системы примет следующий вид:

Нужные переменные Х4 и Х5 можно рассматривать, как свободные переменные, чтобы выразить с их помощью базисные переменные. Для этого данные переменные следует приравнять к нулю. Таким образом, получим базисное решение системы.

 В связи с тем, что в базисном решении отсутствуют отрицательные значения, полученное решение можно считать опорным. Для того чтобы получить частное решение, требуется задать какие-либо значения Х4 и Х5. Например, они равны 1. Тогда:

Примеры решения систем линейных алгебраических уравнений методом Гаусса-Жордана