Вычисление площади правильной треугольной пирамиды
Вычисление площади правильной треугольной пирамиды
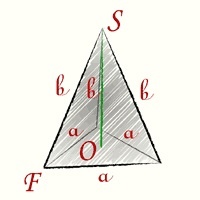
Правильная треугольная пирамида (тетраэдр) — это многогранник, в основании которого лежит правильный треугольник со сторонами a и боковыми гранями в виде равнобедренных треугольников с основанием a и сторонами b.
Площадь поверхности такой фигуры складывается из площадей основания многогранника и трех боковых граней. В записи на математический язык это выглядит так:
\((1)\;S=S_{осн}+3\times S_{бок}\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Нахождение площади основания пирамиды
Поскольку правильный тетраэдр основан на треугольнике, для определения площади основания рассматриваемого многогранника воспользуемся формулой нахождения площади треугольника:
\(S=\frac12ah\)
Значение переменных: a — длина стороны равностороннего треугольника, h — его высота.
Далее произведем подстановку формулы вычисления высоты правильного треугольника и получим искомое выражение:
\((2)\;S_{осн}=\frac{\sqrt3}4a^2\)
Вычисление площади боковых граней и полной поверхности
Боковые грани правильной треугольной пирамиды представлены тремя равнобедренными треугольниками. Выведем формулу расчета площади каждого из них из классического способа вычисления площади треугольника:
\(S=\frac12ah\)
Здесь переменная a обозначает основание треугольника, h — его высоту.
Теперь выполним подстановку выражения, с помощью которого находится высота треугольника с одинаковыми бедрами, и получим уравнение определения площади равнобедренного треугольника:
\((3)\;S_{бок}=\frac{a\sqrt{b^2-\frac{a^2}4}}2\)
В этом случае b — это боковые ребра треугольника, равные между собой.
Подставим в выражение (1) формулы (2) и (3) и получим уравнение, с помощью которого рассчитывается площадь полной поверхности правильного тетраэдра:
\(S=\frac{\sqrt3}4a^2+\frac32\times a\sqrt{b^2-\frac{a^2}4}\)
Примеры задач с решением
Задача
Дано
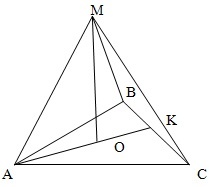
Правильный тетраэдр MABC с вершиной М. Высота основания AK=3 см.
∠MAB=∠MAC=∠MBA=∠MBC=∠MAB=∠MCA=∠MCB=45°. Необходимо вычислить площадь пирамиды MABC.
Решение
В основании правильного тетраэдра лежит равносторонний треугольник с известной длиной высоты. Применим свойство правильного треугольника, состоящее в следующем:
\(h=\frac{\sqrt3}2a\)
Преобразуем данное выражение так, чтобы вывести формулу стороны a:
\(a=\frac h{\frac{\sqrt3}2}\)
Теперь найдем a:
\(a=\frac3{\frac{\sqrt3}2}=\frac{3\times2}{\sqrt3}=\frac6{\sqrt3}\)
Подставим полученное выражение в формулу нахождения площади основания правильного многогранника с тремя боковыми гранями:
\(S_{осн}=\frac{\sqrt3}4\times\left(\frac6{\sqrt3}\right)^2=\frac{\sqrt3}4\times\frac{6^2}{\sqrt3^2}=\frac{36\sqrt3}{4\times3}=3\sqrt3\)
Далее необходимо найти площадь боковых граней тетраэдра. Для этого произведем вычисление высоты MK. Так как угол между гранью и основанием пирамиды равен 45°, то ∠OKM=45°, следовательно:
\(\frac{OK}{MK}=\cos\left(45^\circ\right)=\frac{\sqrt2}2\)
По свойству правильного треугольника, отрезок OK равен радиусу вписанной в ΔABC окружности.
Найдем ее по соответствующей формуле:
\(OK=r=\frac{\sqrt3}6a=\frac{\sqrt3}6\times\frac6{\sqrt3}=\frac{6\sqrt3}{6\sqrt3}=1\)
Подставим найденную величину в отношение ОК к МК:
\(\frac{OK}{MK}=\frac{\sqrt2}2\)
\(\frac1{MK}=\frac{\sqrt2}2\)
Из данной пропорции выведем выражение, по которому можно определить длину высоты MK:
\(MK=\frac2{\sqrt2}\)
Теперь, когда известны основание и высота равнобедренного треугольника, составляющего боковую грань пирамиды MABC, подставим значения в классическую формулу нахождения площади треугольника:
\(S_{бок}=\frac12ah=\frac12\times\frac6{\sqrt3}\times\frac2{\sqrt2}=\frac{1\times6\times2}{2\times\sqrt3\times\sqrt2}=\frac{12}{2\sqrt6}=\frac6{\sqrt6}\)
Суммируем площадь основания и боковых граней пирамиды:
\(S_{MABC}=3\sqrt3+3\times6\sqrt6=3\sqrt3+18\sqrt6\)
Ответ, выраженный в квадратных сантиметрах: \(3\sqrt3+18\sqrt6\;(см^2)\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так