Как найти площадь трапеции
Что такое площадь трапеции
Трапеция — четырехугольник, две стороны которого, называемые основаниями, параллельны друг другу, а две другие стороны — нет.
Вычисление площади трапеции входит в раздел геометрии, который называется планиметрия и занимается фигурами на плоскости.
Площадь трапеции, как и любой другой геометрической фигуры — это часть плоскости, ограниченная периметром и измеряемая в квадратных единицах.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В формулах основания обозначаются буквами a и b, боковые стороны — с и d.
Способы нахождения площади
Существует более двадцати способов вычисления площади трапеции. Выбор способа расчета зависит от известных данных, которые можно подставить в формулу, и от типа самой трапеции: она может быть равнобедренной (равнобокой) или прямоугольной, тогда задача упростится.
Например, если трапеция равнобедренная, вычислить длину ее сторон можно, разбив ее на прямоугольник и два прямоугольных треугольника.
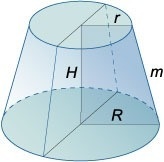
Если трапеция прямоугольная, легко запомнить соотношение ее сторон, пользуясь формулами для усеченного конуса, который образуется при ее вращении вокруг ее боковой стороны, находящейся под прямым углом к основаниям:
Стороны такой трапеции, наглядно видные на схеме, связаны следующим соотношением:
\(H = \sqrt{m^{2} - (R – r)^{2}}.\)
Но большинство формул подходит и для разносторонних трапеций. Если задача практическая и трапеция имеет материальную форму, основания, боковые стороны, высоту и диагонали легко измерить с помощью линейки.
Формулы для вычисления площади равнобедренной и неправильной трапеций
По длине оснований и высоте
Площадь трапеции равна произведению половины суммы оснований на высоту:
\(S = \frac{1}{2} (a+b) \times h.\)
Через длины всех сторон (Формула Герона)
Чтобы посчитать площадь через длины сторон, можно воспользоваться следующей формулой:
\(S = \frac{1}{2} (a+b) \times \sqrt{c^{2} - (\frac{(a - b)^{2} + c^{2} - d^{2}}{2 (a — b)})^{2}}.\)
Существует более простая формула, известная, как формула Герона. Для облегчения ее запоминания вводится р, полусумма всех четырех сторон:
\(p = \frac{1}{2} (a+b+c+d).\)
Формула Герона выглядит так: \(S = \frac{a + b}{\left|a\;-\;b\right|} \times \sqrt{(p - a) (p - b) (p - a - c) (p - a — d)}.\)
Через диагонали и угол между ними
\(S = \frac{1}{2}\times d_{1} \times d_{2} \times \sin\alpha.\)
Здесь \(d_{1}\) и \(d_{2}\) — диагонали, а \(\alpha\) — угол, образованный ими.
Через радиус вписанной окружности
Вписать окружность в трапецию можно только тогда, когда сумма ее оснований равна сумме боковых сторон.
Площадь любой трапеции можно найти через радиус вписанной окружности, зная длину оснований:
\(S = (a + b) \times r.\)
Площадь равнобокой трапеции также можно найти через круг, вписанный в нее. Для этого нужно знать радиус этого круга, а также угол \(\alpha\) при основании.
\(S = \frac{4r^{2}}{\sin\alpha}.\)
Через среднюю линию, боковую сторону и угол при основании
Такой способ нахождения площади подходит только для равнобоких трапеций. В этой формуле средняя линия обозначается буквой m, боковая сторона — буквой с, а угол при основании — \(\alpha\). Зная длину средней линии и боковой стороны, достаточно найти синус угла и умножить эти значения друг на друга:
\(S = m \times c \times \sin\alpha.\)
Примеры решения задач
Найти площадь трапеции, размер одной диагонали которой равен 6 см, второй — 9 см, а угол между ними — \(30^\circ.\)
Решение:
Подставим известные данные в формулу:
\(S = \frac{1}{2}\times d_{1} \times d_{2} \times \sin\alpha\)
Получим:\(S = \frac{1}{2}\times 6 \times 9 \times \sin30^\circ = 13,5. \)
Ответ: 13,5 \(см^{2}.\)
Параллельные стороны плоской геометрической фигуры равны 9 и 5 см. Расстояние между ними — 7 см. Найти площадь фигуры.
Решение:
Подставим известные данные в формулу:
\(S = \frac{1}{2} (a+b) \times h\)
Получим:
\(S = \frac{1}{2} (9+5) \times 7 = 49.\)
Ответ: 49 \(см^{2}\).
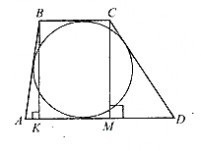
Найти площадь трапеции, если известны длины непараллельных сторон — 13 и 15 см, а также разность длин оснований — 14 см. В трапецию вписана окружность.
Решение:
Одно из основных свойств трапеции — в нее можно вписать окружность, если сумма оснований равна сумме боковых сторон. Следовательно, если представить две проведенные высоты, как на рисунке, АК + МD = АD — BC = 14.
AK = 14 — MD.
Поскольку углы К и М являются прямыми, воспользуемся теоремой Пифагора:
\(AB^{2} = AK^{2} + BK^{2}.\)
\(BK^{2} = AB^{2} — AK^{2}.\)
\(CD^{2} = CM^{2} + MD^{2}.\)
\(CM^{2} = CD^{2} — MD^{2}.\)
\(BK = CM.\)
\(AB^{2} — AK^{2} = CD^{2} — MD^{2}.\)
Подставим числовые значения:
\(13^{2} — (14 — MD)^{2} = 15^{2} — MD^{2}.\)
MD = 9 см.
\(CM^{2} = CD^{2} — MD^{2}.\)
\(CM = \sqrt{CD^{2} — MD^{2}} = \sqrt{15^{2} — 9^{2}} = 12.\)
Теперь, вычислив высоту, мы можем воспользоваться формулой:
\(S = \frac{1}{2} (a+b) \times h\)
Подставим в нее известные значения, получив:
\(S = \frac{28 \times 12}{2} = 168.\)
Ответ: 168 \(см^{2}\).
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так