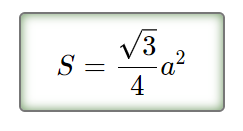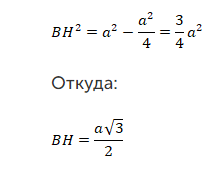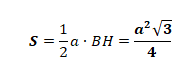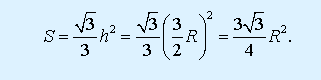Как найти площадь равностороннего треугольника
В задачах часто найти правильное решение можно зная площадь треугольника. Выбор формулы для этого действия зависит от его характеристик.
Что такое равносторонний или правильный треугольник
Для треугольника, как для геометрической фигуры, обязательным условием является наличие трех сторон, образующих три угла. В зависимости от соотношения длин сторон и величин углов треугольники подразделяются на:
- равносторонние;
- разносторонние;
- прямоугольные;
- равнобедренные.
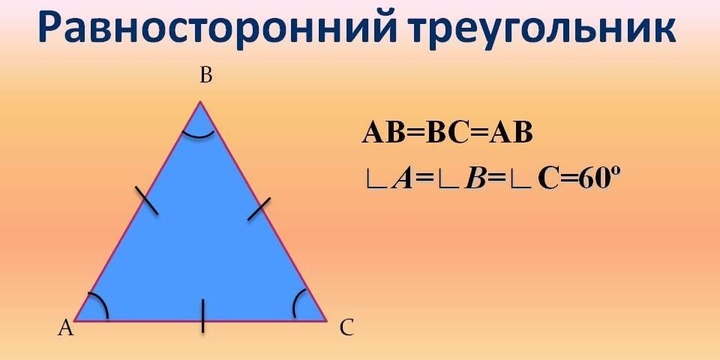
Треугольник, имеющий все стороны одинаковой длины, носит название равностороннего.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: ru-static.z-dn.net
Второе название такой фигуры — «правильный». Это самый простой правильный многоугольник, в котором биссектриса полностью совпадает с медианой и высотой.
Одной из важных характеристик равностороннего треугольника является та, что все три его внутренних угла равны и составляют 60о каждый. Это еще раз подтверждает, что сумма внутренних углов треугольника равна 180о.
В любой равносторонний треугольник может быть вписана окружность. При этом ее центральная точка непременно совпадет с тем местом, в котором пересекаются высота и медиана этого треугольника.
Площадь равностороннего треугольника через сторону, формула
Учитывая названные свойства треугольника с равными сторонами, высчитать его площадь можно несколькими способами:
- через длину стороны:
- через высоту;
- используя треугольник, вписанный в окружность.
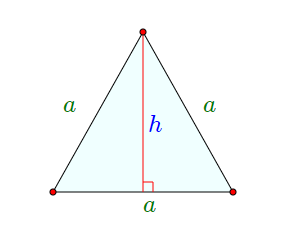
Чтобы понять формулы для вычисления, рассмотрим рисунок:
Источник: kalk.top
На данном рисунке условные обозначения следующие:
Источник: kalk.top
Чтобы находить площадь равностороннего треугольника через его сторону, можно использовать формулу:
Источник: kalk.top
Высота h, являющаяся одновременно биссектрисой и медианой, делит нижнюю сторону на две половины. Длину одной половину можно выразить \(a/2\).
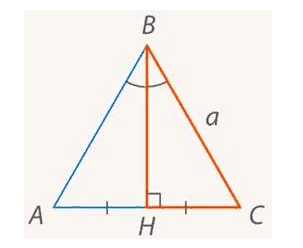
Кроме этого, она образует два прямоугольных треугольника, один из которых рассмотрим отдельно:
Источник: interneturok.ru
Используя теорему Пифагора, получаем равенство:
Источник: interneturok.ru
Из приведенных выражений легко вывести формулу для нахождения площади, если известна длина стороны:
Источник: interneturok.ru
Доказательство данной формулы настолько очевидно, что может быть легко восстановлено в памяти в любой момент.
Площадь равностороннего треугольника через высоту, формула
Рассчитать такую величину, как площадь треугольника со сторонами одной длины, можно не только зная это значение, но и используя саму высоту.
Согласно теореме о площади любого треугольника, она равна произведению двух величин: длины стороны и высоты, которая к ней проведена. Для равностороннего треугольника такое утверждение также справедливо.
\(S=(1/2)ah\)
В ходе доказательства этой формулы используется алгоритм построения из имеющегося треугольника параллелограмма, нахождения его площади и деления пополам.
Площадь равностороннего треугольника, вписанного в окружность
Источник: www.resolventa.ru
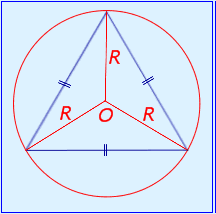
Основанием для выведения формулы площади равностороннего треугольника через радиус описанной вокруг него окружности, является утверждение, что:
В треугольнике с равными сторонами центр окружности, в которую вписан этот треугольник, является точкой пересечения его медианы, высоту и биссектрисы одновременно.
Тогда равенство \(2/3h=R\) подтверждено.
Следовательно, формулировка выражения для нахождения площади через радиус описанной окружности выглядит так:
Источник: www.resolventa.ru
Примеры решения задач
Периметр равностороннего треугольника составляет 36 см. Какова площадь данной геометрической фигуры?
Решение.
Первым действием будет нахождение длины стороны через известных периметр: 36:3=12 (см)
Второе действие основано на формуле: \(S=(a2√3)/4 = 144√3/4=36√3\)
Ответ: \(36√3\)
Площадь равностороннего треугольника равна \(25√3\). Какова длина его стороны?
Решение: Используя формулу площади равностороннего треугольника через известную длину стороны, получаем выражение:
\(S=(a2√3)/4\)
\(25√3=(a2√3)/4\)
\(25=a2\)
a=5
Ответ: сторона треугольника равна 5.
Площадь равностороннего треугольника равна \(49√3\). Чему равна высота этой фигуры?
Решение.
Первым действием находим длину его стороны:
\(S=(a2√3)/4\)
\(49√3=(a2√3)/4\)
\(49=a2\)
a=7
Во втором действии применяем формулу: \(h=a√3/2=7√3/2=3,5√3\)
Ответ: высота равна \(3,5√3\)
Радиус окружности, описанной вокруг равностороннего трегольника, равен 10. Найти площадь этого треугольника и длину его стороны.
Решение:
В первом действии применяем формулу:
\(S=3√3/4*R2\)
\(S=300√3/4=75√3\)
С другой стороны:
\(S=a2√3/4\)
\(75√3=a2√3/4\)
Сокращая √3, получаем: \(4a2=75\)
a=√18,75
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так