Площадь треугольника через радиус описанной окружности
Как найти площадь треугольника через радиус описанной окружности
Описанной около выпуклого многоугольника окружностью называют такую окружность, которая пересекает каждую из вершин рассматриваемого многоугольника.
Если около некоторого многоугольника описана окружность, то данный многоугольник является вписанным в эту окружность. Существует правило, согласно которому в выпуклый многоугольник можно также вписать какую-либо окружность. Для этого требуется, чтобы все серединные перпендикуляры сторонам многоугольника обладали единственной точкой пересечения. Данную точку называют центром вписанной в многоугольник окружности.
Центр окружности, которая описана около многоугольника, расположен на одинаковом расстоянии от всех вершин рассматриваемого многоугольника. При этом отрезок, один конец которого совпадает с центром окружности, а второй — с любой из вершин многоугольника, равен радиусу описанной окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Рассмотрим наглядный пример:
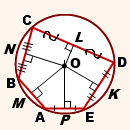
На рисунке изображен многоугольник с пятью углами ABCDE. Около этого пятиугольника описана окружность, центр которой обозначен О, а радиус равен R. Таким образом, ABCDE представляет собой вписанный пятиугольник, а O является точкой, в которой пересекаются серединные перпендикуляры, проведенные к сторонам ABCD. Запишем следующие соотношения:
\(AP = PE,OP \bot AE\)
\(AM = MB,OM \bot AB\)
\(BN = NC,ON \bot BC\)
\(CL = LD,OL \bot CD\)
\(DK = KE,OK \bot DE\)
Заметим, что точка O находится на одинаковом расстоянии, то есть равноудалена, от каждой из вершин рассматриваемого многоугольника с каким-то периметром:
Данное расстояние между точкой О и какой-либо вершиной соответствует радиусу описанной окружности:
OA=OB=OC=OD=OE=R
Окружность можно описать около любого треугольника. А, к примеру, около выпуклого четырехугольника имеется возможность описать окружность только в том случае, если противолежащие углы данной геометрической фигуры в сумме дают 180°.
Если имеется некий правильный многоугольник, то есть равносторонний, вокруг него можно описать окружность. Также в какой-либо правильный многоугольник представляется возможным вписать окружность. В данном случае центры вписанной и описанной окружности совпадают с центром правильного многоугольника.
Отсутствует стандартная формула, с помощью которой можно определить радиус окружности, описанной около многоугольника. Подобная формула предусмотрена для вычисления радиуса вписанной окружности. Поэтому радиус описанной окружности соответствует радиусу окружности, которая описана около какого-либо из треугольников с вершинами, являющимися вершинами описанного многоугольника.
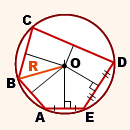
К примеру, представим, что имеется некий многоугольник ABCDE с пятью углами, около которого описана окружность. Радиус данной окружности равен радиусу окружности, описанной около какого-либо из перечисленных треугольников:
- ABC;
- ABD;
- ABE;
- BCD;
- BCE;
- ACD;
- ADE и так далее.
Частные случаи составления формул для расчета радиуса описанной окружности:
- правильные многоугольники;
- треугольники;
- прямоугольники.
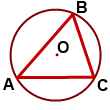
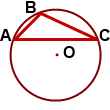
Описанная около треугольника окружность — это окружность, на которой расположены все вершины данного треугольника. В этом случае треугольник называют треугольником, вписанным в эту окружность.
Заметим, что:
\(OA=OB=OC=R\)
Расстояние, на которое удалена каждая из вершин треугольника от центральной точки описанной окружности, соответствует радиусу данной окружности. Заметим, что окружность допустимо описать около какого-либо треугольника без ограничений. Описанная около треугольника окружность обладает центром, совпадающим с точкой, в котором пересекаются серединные перпендикуляры, проведенные к граням треугольника. Данные отрезки перпендикулярны относительно сторон треугольника и пересекают середины этих сторон.
Предположим, что имеется некий треугольник с острыми углами. Если описать окружность около такой геометрической фигуры, то центр окружности будет расположен в ее внутреннем пространстве.
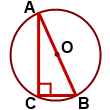
Представим, что имеется некий прямоугольный треугольник. Если описать около такой геометрической фигуры окружность, то ее центр будет расположен на середине гипотенузы.
Около треугольника с тупым углом также допустимо описать окружность. При этом центр данной окружности окажется вне геометрической фигуры. В данном случае центральная точка окружности расположена напротив тупого угла треугольника, за большей стороной.
Теорема с доказательством
Определить площадь треугольника можно путем деления результата от произведения сторон этого треугольника на четыре радиуса окружности, которая описана около данного треугольника.
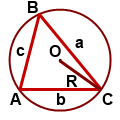
Докажем записанную теорему. Для этого представим, что существует некий треугольник АВС. Опишем около данного треугольника окружность (O; R). Обозначим стороны треугольника таким образом:
\(AB=c, BC=a, AC=b.\)
Нужно представить доказательство того, что:
\({S_{\Delta ABC}} = \frac{{abc}}{{4R}}\)
Изобразим данные треугольник и окружность для наглядности:
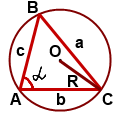
Ведем обозначение угла А. Пусть:
\(\angle A= \alpha\)
Вспомним, что вычислить площадь треугольника можно по двум сторонам и углу между ними, как половину от результата умножения пары сторон треугольника на синус угла, расположенного между ними.
Формула имеет вид:
\(S = \frac{1}{2}ab\sin \alpha\)
Применительно к нашему случаю, получим:
\({S_{\Delta ABC}} = \frac{1}{2}AC \cdot AB \cdot \sin \angle A = \frac{1}{2}bc\sin \alpha.\)
Далее требуется воспользоваться теоремой синусов, вернее, ее следствием. Заметим, что стороны треугольника относятся к синусу противолежащего угла, как радиус, описанной окружности около данного треугольника, умноженный на два:
\(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin \beta }} = \frac{c}{{\sin \gamma }} = 2R\)
Тогда:
\(R = \frac{a}{{2\sin \alpha }}.\)
С помощью данной формулы можно представить расчет синуса угла \(\alpha\):
\(\sin \alpha = \frac{a}{{2R}}\)
При подстановке полученного выражения в начальную формулу имеем:
\({S_{\Delta ABC}} = \frac{1}{2}bc\sin \alpha = \frac{1}{2}bc \cdot \frac{a}{{2R}} = \frac{{abc}}{{4R}}.\)
Теорема доказана.
Примеры задач
Ранее получилось доказать теорему о площади треугольника, вычисляемой с помощью радиуса описанной окружности. Запишем формулу, отражающую смысл этой теоремы:
\(S = \frac{{abc}}{{4R}}\)
Используя данную формулу, можно решать задачи по геометрии. Приведем несколько типичных примеров таких заданий.
Дан равнобедренный треугольник с боковыми гранями, равными 50. Основание фигуры составляет 80. Требуется определить радиус, которым обладает описанная около данного треугольника окружность.
Решение
Найдем радиус окружности через площадь треугольника:
\(R=\frac{abc}{4S}\)
С помощью формулы Герона рассчитаем площадь:
\(S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{90(90-50)^2(90-80)}=900\)
В результате:
\(R=\frac{90\cdot 50\cdot 50}{4\cdot 900}=62,5\)
Ответ: 62,5.
Имеется некий треугольник АВС. Одна из его сторон АВ составляет 28. Угол напротив этой стороны С составляет 150 градусов. Требуется определить радиус окружности, которая описана около данного треугольника.
Решение
Воспользуемся теоремой синусов и запишем:
\(\frac{AB}{sinC}=2R\)
\(\frac{28}{sin150^{\circ}}=2R\)
\(\frac{28}{\frac{1}{2}}=2R\)
В результате:
R=28.
Ответ: 28.
Дан некий треугольник АВС. Градусная мера угла С составляет 90 градусов, а стороны равны:
BC=16;
AC=30.
Нужно вычислить, каким радиусом обладает описанная около данного треугольника окружность.
Решение
Заметим, что в условии задачи речь идет о прямоугольном треугольнике. Тогда диаметр описанной около такого треугольника окружности является гипотенузой. Запишем:
\(R=\frac{AB}{2}\)
Согласно теореме Пифагора:
\(AB=\sqrt{BC^2+AC^2}=\sqrt{16^2+30^2}=34\)
В результате:
\(R=\frac{AB}{2}=\frac{34}{2}=17\)
Ответ: 17.
Около некого правильного треугольника описана окружность с радиусом \(17\sqrt{3}\). Нужно вычислить сторону данного треугольника.
Решение
Согласно теореме косинусов:
\( \frac{AB}{sinC}=2R\)
\(\frac{AB}{sin60^{\circ}}=2\cdot 17\sqrt{3}\)
\(\frac{AB}{\frac{\sqrt3}{2}}=34\sqrt{3}\)
В таком случае:
AB=51
Ответ: 51.
Имеется некий правильный треугольник, сторона которого равна \(7\sqrt3\). Требуется вычислить радиус окружности, описанной около этой геометрической фигуры.
Решение
Согласно теореме синусов:
\(\frac{AB}{sinC}=2R\)
\(\frac{7\sqrt3}{sin60^{\circ}}=2R\)
14=2R
В результате:
R=7
Ответ: 7.
Имеется окружность, на которой расположены точки А, В, С. Эти точки образуют три дуги с градусными мерами в соотношении 1:6:11. Нужно вычислить, какую градусную меру имеет самый большой угол треугольника АВС.
Решение
Обозначим дугу АВ за переменную х. В таком случае:
BC=6x
AC=11x
Далее запишем следующее соотношение:
x+6x+11x=360
18x=360
x=20
В результате:
\(\breve{AC}=20^{\circ}\cdot 11=220^{\circ}\)
Вспомним, что вписанный угол соответствует ½ дуги, на которую этот угол опирается. В результате:
\(\angle ABC=\frac{220^{\circ}}{2}=110^{\circ}\)
Ответ: \(110^{\circ}.\)
Даны треугольник и описанная около него окружность с радиусом 1. Одна из сторон треугольника равна \(\sqrt2\). Требуется определить градусную меру острого угла треугольника, который расположен напротив этой стороны.
Решение
Согласно теореме синусов:
\(\frac{a}{sin \alpha}=2R\)
\(\frac{\sqrt2}{sin \alpha}=2\cdot 1\)
\(sin\alpha=\frac{\sqrt2}{2}\)
\(\alpha=45^{\circ}\)
Согласно условию задачи, \(\alpha\) является острым углом.
Ответ: \(45^{\circ}\).
Углы некого четырехугольника составляют \(56^{\circ}\) и \(99^{\circ}\). Эта фигура вписана в окружность. Требуется определить самый большой из неизвестных углов.
Решение
Исходя из условия задачи, сделаем вывод о том, что данные углы не противоположны друг другу. В противном случае, эти углы в сумме составляли бы \(180^{\circ}\).
При \(\angle A=99^{\circ}\), то \(\angle C=180^{\circ}-99^{\circ}=81^{\circ}\)
При \(\angle B=56^{\circ}\), то \( \angle D=180^{\circ}-56^{\circ}=124^{\circ}\)
Тогда угол D является самым большим.
Ответ: \(124^{\circ}.\)
Имеется четырехугольник ABCD. Вокруг него описана окружность. Градусная мера угла АВС составляет \(38^{\circ}\), а угла CAD равна —\(38^{\circ}\). Нужно определить угол ABD в градусах.
Решение
По условию задачи:
\(\angle ABC=38^{\circ}\)
В результате, дуга ADC составит \(76^{\circ}.\)
Также в условии дано:
\(\angle CAD=33^{\circ}\)
Тогда дуга DC равна \(66^{\circ}.\)
В итоге получим:
\(\breve{AD}=\breve{ADC}-\breve{DC}=76^{\circ}-66^{\circ}=10^{\circ}\)
Таким образом:
\(\angle ABD=5^{\circ}\)
Ответ: 5.
Имеется квадрат, около которого описана окружность с радиусом \(45\sqrt2\). Требуется вычислить сторону квадрата.
Решение
Диаметр окружности равен диагонали BD квадрата, около которого она описана. Обозначим сторону квадрата за х. Используем теорему Пифагора и запишем:
\(x^2+x^2=(90\sqrt2)^2\)
\(2x^2=90^2\cdot 2\)
\(x^2=90^2\)
\(x=90\)
Ответ: 90.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так