Вычисление площади треугольника при помощи радиуса вписанной окружности
Формула 1Площадь треугольника через радиус вписанной окружности
Как найти, теорема и доказательство, формула
Площадь треугольника равна произведению полупериметра данного треугольника на радиус вписанной в него окружности.
S=pr где p — полупериметр,
r — радиус вписанной окружности,
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
a, b, c — стороны треугольника.
Доказательство:
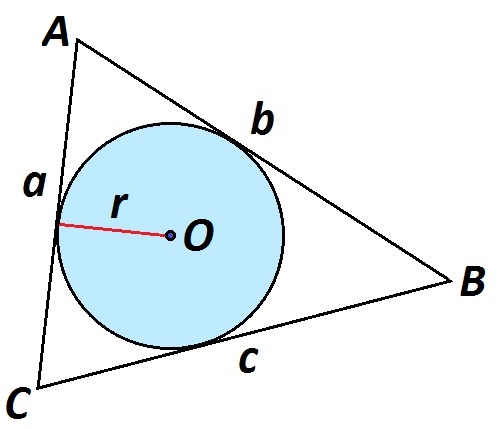
Пусть у ΔABC стороны равны a, b, c. AС=а, АВ=b, ВС=с. В ΔABC вписана окружность с центром в точке О и радиусом r.
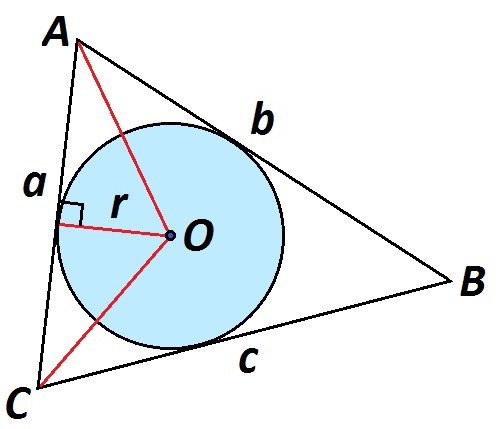
Проведем отрезки ОА и ОС. Радиус r является высотой ΔАОС, проведенной к АС, по свойству касательной к окружности и ее радиуса. Так как площадь треугольника равна половине произведения основания и проведенной к этому основанию высоты,
\(S_{\Delta AОC}=\frac12a·r.\)
Таким же образом найдем площади треугольников АОВ и ВОС.
\(S_{\Delta AОВ}=\frac12b·r, \)
\(S_{\Delta BОC}=\frac12c·r.\)
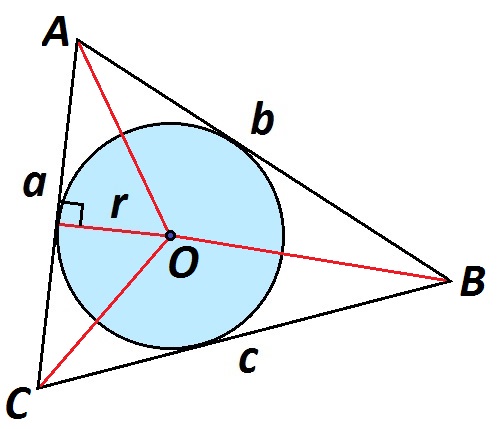
ΔABC разбит отрезками ОА, ОВ и ОС на ΔAОВ, ΔAОC и ΔBОC, и его площадь равна сумме площадей данных треугольников.
\(S_{\Delta AВС}=S_{\Delta AОC}+S_{\Delta AОВ}+S_{\Delta BОC},\)
\(S_{\Delta AВС}=\frac12a·r+\frac12b·r+\frac12c·r,\)
\(S_{\Delta AВС}=frac12r\left(а+b+c\right).\)
Периметр ΔABC равен сумме его трех сторон, а полупериметр равен \(\frac{\left(a+b+c\right)}2. \)
Отсюда делаем вывод, что \(S_{\Delta AВС}=pr\), где p — полупериметр.
Теорема доказана.
Примеры решения задач с ответами
Дано: ΔDEF — равнобедренный, DE=EF. В ΔDEF вписана окружность, к которой проведена касательная КМ.
При этом КМ||EF.
\(DK=\frac38·EF. S_{\Delta DEF}=12 см^2.\)
Найти: радиус вписанной окружности.
Решение:
Пусть N — точка касания окружности и КМ, Р — точка касания окружности и DE, Н — точка касания окружности и DF.
Обозначим DE=EF=а, DH=HF=b.
Тогда DP=b, так как DP=DH.
MN=MH.
KP=KN.
DP=DK+KP=DK+KN.
DH=DM+MH=DM+MN.
DP=DH.
ΔDKM и ΔDEF подобны.
Пусть \(p_1\) и p — их полупериметры. Тогда полупериметр \(ΔDKM p_1=DP=DH=b.\)
Полупериметр ΔDEF p=DE+DH=a+b
\(p_1:p=DK:DE=3:8\)
b=3a/5
Так как квадрат гипотенузы равен сумме квадратов катетов, то \(EH^2=DE^2-DH^2=a^2-(3a/5)^2. \)
Так как \(S_{\Delta DEF}=EH·DH\), то \(12=b·4a/5=3a/5·4a/5. a=5, b=3.\)
Следовательно, радиус вписанной окружности \(r=\frac{S_{\Delta DEF}}p=\frac{12}{a+b}=\frac32 (см).\)
Ответ: радиус вписанной окружности равен 1,5 см.
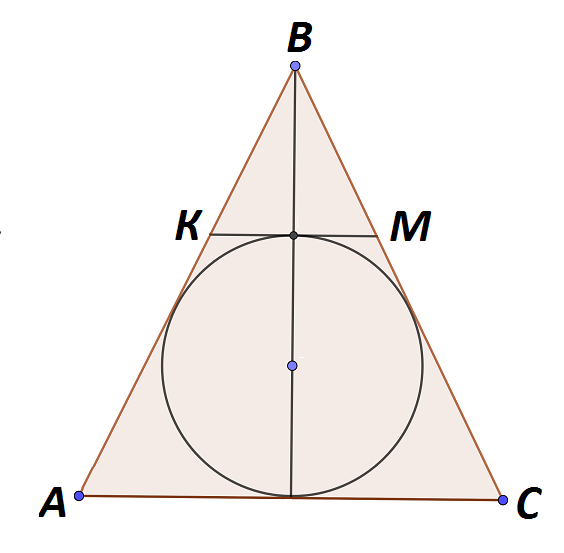
Дано: ΔАВС — равнобедренный. Его основание АС равно 12 см, а высота, проведенная к основанию — 8 см. В треугольник вписана окружность, к которой проведена касательная КМ, параллельная основанию.
Найти: КМ.
Решение:
ΔАВС и ΔКВМ подобны. Найдем коэффициент их подобия.
\(S_{\Delta АВС}=12·8=96 (см^2). \)
По теореме Пифагора найдем АВ и затем вычислим р — полупериметр ΔАВС, р=32 (см).
Радиус вписанной окружности \(r=\frac{S_{\Delta АВС}}р=96:32=3 (см).\)
Диаметр вписанной окружности равен 6 см, а высота ΔКВМ, проведенная к КМ равна 2 см.
Коэффициент подобия ΔАВС и ΔКВМ равен \(\frac14.\)
Значит \(КМ=\frac14·АС=3 (см).\)
Ответ: КМ=3 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так