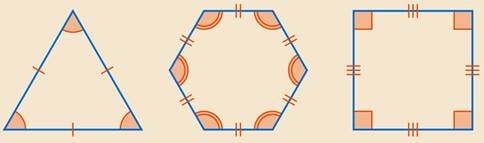
Определение правильного многоугольника

Правильный многоугольник — что значит

Многоугольники различают по количеству сторон и углов.

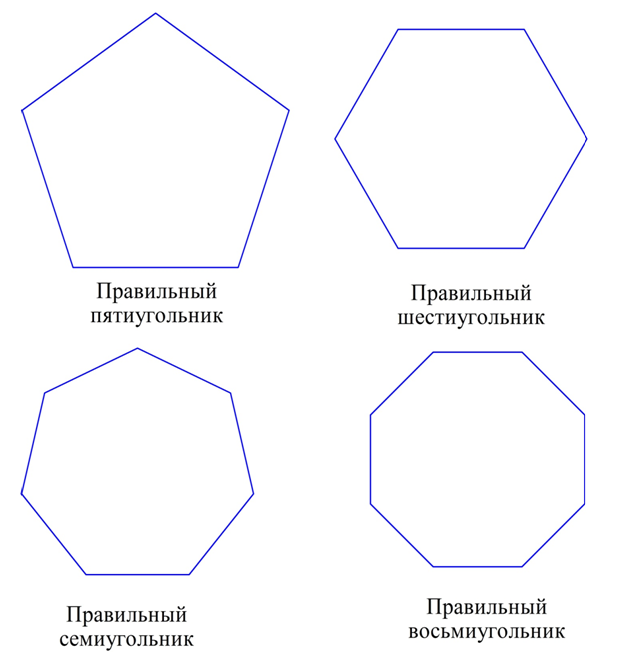
Существует несколько разновидностей правильных многоугольников. К наиболее известным относят равносторонний треугольник, который обладает тремя одинаковыми сторонами и углами, равными 60 градусов. В связи с этим данную геометрическую фигуру называют правильным треугольником.

Квадрат обладает четырьмя одинаковыми сторонами и углами по 90 градусов. Такую геометрическую фигуру называют правильным четырехугольником.

При каком-либо заданном числе n, начиная с n=3, можно построить правильный n-угольник. Примеры таких многоугольников изображены на рисунке:

Признаки и свойства правильного многоугольника

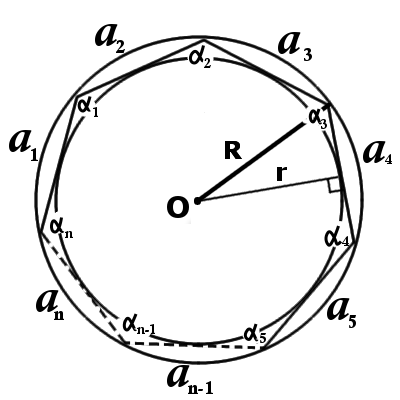
Многоугольник можно считать правильным в том случае, когда все его стороны и углы одинаковы. Таким образом, должно выполняться правило:

\(a_{1} = a_{2} = a_{3} = … = a_{n-1} = a_{n}\)

\(\alpha _{1} = \alpha _{2} = \alpha _{3} = … = \alpha _{n-1} = \alpha _{n}\)

Существуют основные свойства, характерные для правильных многоугольников.

1. Все стороны правильного многоугольника равны, то есть: \(a_{1} = a_{2} = a_{3} = … = a_{n-1} = a_{n}\)
2. Углы правильного многоугольника равны, то есть: \(\alpha _{1} = \alpha _{2} = \alpha _{3} = … = \alpha _{n-1} = \alpha _{n}\)
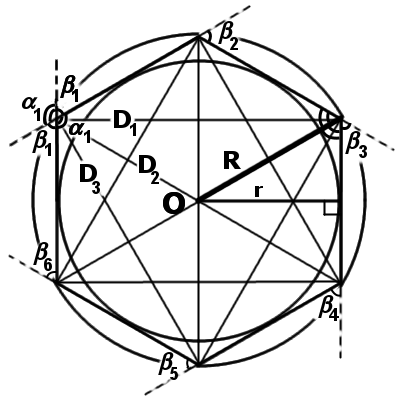
3. Центр вписанной в правильный многоугольник окружности \(O _{B}\) соответствует центру описанной вокруг этого многоугольника окружности \(O _{O}\), что в результате образует центр многоугольника О
4. Сумма всех углов n-угольника составляет: \(180^{0}*(n-2)\)
5. Внешние углы n-угольника в сумме равны 360^{0} или \(\beta _{1} + \beta _{2} + \beta _{3} + … + \beta _{n-1} + \beta _{n} = 360^{0}\)
6. Число диагоналей \(D _{n}\), которыми обладает n-угольник, соответствует половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины, то есть: \(\beta _{1}=\frac{n*(n-3)}{2}\)
7. В правильный многоугольник можно вписать окружность и описать круг. При этом площадь кольца, сформированного данными окружностями, определяется лишь длиной стороны многоугольника, то есть: \(S=\frac{\pi }{4}a^{2}\)
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника О.

Основные свойства, определение правильного n-угольника

Правильный n-угольник представляет собой особый вид многоугольника с равными между собой сторонами и углами.

Существует формула, с помощью которой можно определить его длину при известном радиусе вписанной в него окружности:

\(\alpha =2r*\tan \frac{180^{0}}{n}\)

\(\alpha =2r*\tan \frac{\pi }{n}\)

При этом радиус вписанной окружности n-угольника определяют через длину стороны:

\(r=\frac{a }{2\tan \frac{180^{0}}{n}}\)

\(r=\frac{a }{2\tan \frac{\pi }{n}}\)

Сторону правильного n-угольника можно определить на основании радиуса описанной вокруг него окружности:

\(a=2R*\sin \frac{180^{0}}{n}\)

\(a=2R*\sin \frac{\pi }{n}\)

Таким образом, радиус описанной окружности n-угольника составляет:

\(R=\frac{a}{2\sin \frac{180^{0}}{n}}\)

\(R=\frac{a}{2\sin \frac{\pi }{n}}\)

Площадь правильного n-угольника можно определить, зная длину стороны, по формуле:

\(S=\frac{na^{2}}{4}*ctg\frac{180^{0}}{n}\)

При известном радиусе вписанной окружности, площадь n-угольника равна:

\(S=nr^{2}*\tan \frac{180^{0}}{n}\)

Если известен радиус описанной окружности, то площадь n-угольника определяется по формуле:

\(S=\frac{nR^{2}}{2}*\sin \frac{360^{0}}{n}\)

Периметр правильного n-угольника составляет:

\(P=na\)

Определить угол между сторонами правильного n-угольника можно с помощью формулы:

\(\alpha _{n}=\frac{n-2}{n}*180^{0}\)

Известно, что треугольник можно задать с помощью длин трех его сторон. Однако в случае правильного треугольника необходимо знать только одну длину стороны, так как все правильные треугольники подобны. Таким образом, при отсутствии данных о масштабе или метрики, правильные треугольники эквивалентны друг другу.

Такими же свойствами обладает квадрат, то есть правильный четырехугольник.

В качестве примеров таких геометрических фигур можно рассмотреть правильные пяти, шести и сколь угодно большие n-угольники. Предельным случаем при бесконечно увеличивающемся n является окружность. Для всех таких многоугольников характерны следующие свойства:

• геометрические фигуры задают с помощью одного параметра, то есть длиной элемента;
• рассматриваемые многоугольники подобны всем многоугольникам своего класса.

В геометрии можно встретить разные виды правильных n-угольников. Все они обладают не только одним параметром, с помощью которого задаются, но и характеризуются осями и центром симметрии. Правильный треугольник возможно три раза повернуть вокруг центра. При этом разница между данными положениями отсутствует.

Квадрат можно повернуть таким же способом четыре раза. Предельным случаем является окружность, которую можно повернуть бесконечное число раз, но результат при этом не изменится, то есть данная геометрическая фигура обладает бесконечным количеством осей симметрии.

В природе невозможно найти идеальную окружность или любой другой правильный n-угольник. В реальности предметы рассматривают лишь в качестве их приближений. Однако многие практические задачи характеризуются достаточно точным приближением, что позволяет применять правильные многоугольники в их решении, как полезный инструмент. Свойства таких геометрических фигур изучают и фиксируют.

В дальнейшем при рассмотрении окружности в качестве предельного случая правильных n-угольников эти свойства переносят на нее для получения полезных утверждений не для ломаной, а для гладкой кривой.

Известно, что равносторонний треугольник представляет собой правильный треугольник. Необходимо выяснить, является ли любой равносторонний многоугольник также правильным многоугольником.

В качестве примера можно рассмотреть ромб, имеющий равные стороны. Таким образом, ромб является равносторонним четырехугольником, но не относится к правильным n-угольникам. К данной категории справедливо отнести только квадрат, так как он обладает не только равными сторонами, но и углами, что отличает его от ромба.

Напомним, что правильными многоугольниками являются те, которые имеют равные стороны и равные углы.

В случае треугольника достаточным условием является равенство сторон. Так как из этого следует равенство его углов. При рассмотрении других n-угольников это утверждение не верно.

Формула угла правильного многоугольника

Существует закономерность, согласно которой можно рассчитать угол правильного многоугольника. Известно, что для любого выпуклого n-угольника сумма углов составляет \(180^{0}(n-2)\). Предположим, что угол правильного многоугольника обозначен \alpha. Исходя из того, что у такой геометрической фигуры n углов, и они равны, можно записать следующее равенство:

\(n*\alpha =180^{0}(n-2)\)

Из записанного выражения можно выразить \(\alpha\), то есть записать формулу угла правильного многоугольника:

\(\alpha =\frac{180^{0}(n-2)}{n}\)

В данном случае n обозначает число сторон многоугольника.

Справедливость записанной формулы можно проверить на примере равностороннего треугольника и квадрата. В случае треугольника n=3, а угол составляет \(60^{0}\). Его можно определить по формуле:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(3-2)}{3}=\frac{180^{0}*1}{3}=60^{0}\)

В случае квадрата, у которого n=4, угол равен \(90^{0}\), что легко рассчитать:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(4-2)}{4}=\frac{180^{0}*2}{4}=90^{0}\)

Используя данную закономерность можно определить углы других правильных многоугольников.

Угол правильного пятиугольника равен:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(5-2)}{5}=\frac{180^{0}*3}{5}=108^{0}\)

Угол правильного шестиугольника составляет:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(6-2)}{6}=\frac{180^{0}*4}{6}=120^{0}\)

Угол правильного восьмиугольника равен:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(8-2)}{8}=\frac{180^{0}*6}{8}=135^{0}\)

В случае правильного многоугольника с 50 углами, каждый угол составит:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(50-2)}{50}=\frac{180^{0}*48}{50}=172,8^{0}\)

Далее в качестве примера использования формулы угла правильного n-угольника можно рассмотреть задачу на определение числа сторон у правильного многоугольника, каждый угол которого составляет \(179^{0}.\)

\(\alpha =\frac{180^{0}(n-2)}{n}\)

\(179=\frac{180(n-2)}{n}\)

\(179n=180(n-2)\)

\(179n=180n-360\)

\(179n-180n=-360\)

\(-n=-360\)

\(n=360\)

Таким образом, рассматриваемый правильный многоугольник обладает 360 сторонами.

С помощью формулы угла правильного многоугольника можно определить, существует ли такой правильный многоугольник, угол которого составляет \(145^{0}\). В том случае, когда такая геометрическая фигура существует, формула примет вид:

\(\alpha =\frac{180^{0}(n-2)}{n}\)

\(145=\frac{180(n-2)}{n}\)

\(145n=180(n-2)\)

\(145n=180n-360\)

\(145n-180n=-360\)

\(-35n=-360\)

\(n=\frac{360}{35}=\frac{72}{7}=10\frac{2}{7}\)

Исходя из того, что число сторон является не целым, а дробным, можно сделать вывод о невозможности существования такого многоугольника.