Правило трех сигм
В чем заключается правило трех сигм (3-sigma rule) в статистике
Математическое ожидание — это среднее значение случайной величины. Обозначается как \(\mu\).
Стандартное или среднеквадратичное отклонение — это наиболее частый показатель рассеивания значений величины относительно математического ожидания. Обозначается символом \(\sigma\), который произносится как «сигма».
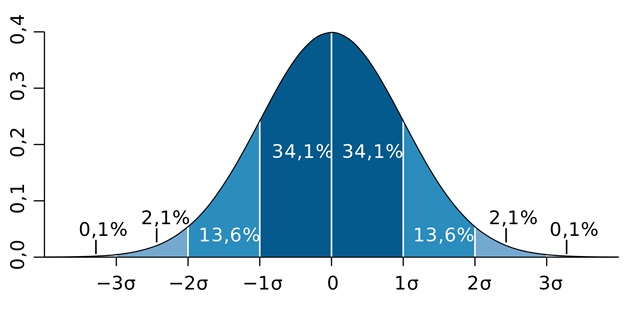
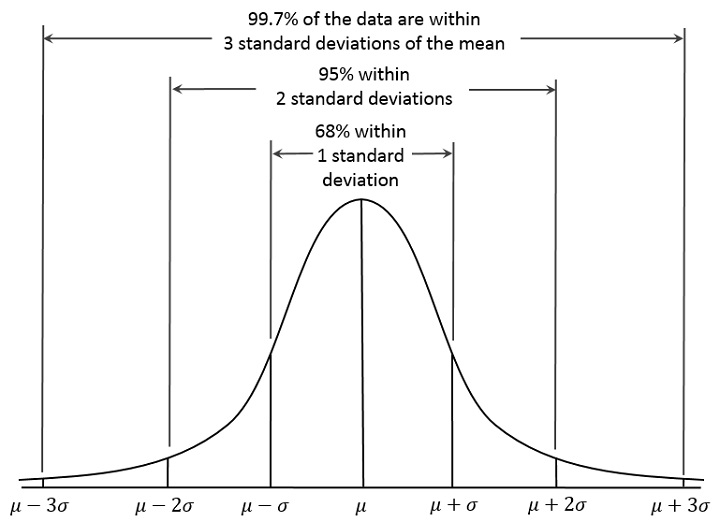
Правило трех сигм заключается в том, что при нормальном распределении практически все значения величины с вероятностью 0,9973 лежат не далее трех сигм в любую сторону от математического ожидания, то есть находятся в диапазоне \(\left[\mu-3\sigma;\;\mu+3\sigma\right]\).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Приблизительно 99,7% всех значений лежат в пределе трех сигм от математического ожидания, около 95% — в пределах двух сигм, а примерно 68% значений лежат в пределах всего одной сигмы.
Те значения, которые выходят за рамки 3 сигм, принято считать грубыми ошибками. Большое количество таких ошибок может свидетельствовать о том, что распределение на самом деле не является нормальным. В этом заключается практическая польза правила 3 сигм.
Нормальное распределение случайной величины
Нормальное распределение (распределение Гаусса) — это такое распределение вероятностей, функция плотности которого совпадает с функцией Гаусса.
\(f\left(x\right)=\frac1{\sigma\sqrt{2\pi}}exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2}\right)\)
где \(\mu\) — значение математического ожидания, \(\sigma\) – величина среднеквадратического отклонения, \(\sigma^2\) — дисперсия распределения.
Функция плотности — это функция, которая характеризует сравнительную вероятность реализации определенных значений случайной переменной или переменных.
Иными словами, функция плотности показывает, с какой вероятностью случайное значение будет равно заданному. Чем «выше» значение по оси ординат, тем больше вероятность, что случайное значение будет равно данному по оси абсцисс. Таким образом, на графике нормального распределения наиболее вероятно то значение, которое совпадает с точкой максимума. А те значения, которые находятся в «основании» графика, то есть находятся низко по оси Y, менее вероятны.
Нормальное распределение величины центрировано и нормировано.
График нормального распределения тесно связан с центральной предельной теоремой (ЦПТ). Согласно ЦПТ, сумма достаточно большого количества слабо зависимых случайных величин имеет распределение, близкое к нормальному.
Нормальное распределение не является абстрактным понятием. Ему соответствуют некоторые характеристики живых организмов в популяции, отклонение от мишени при стрельбе, измерения и их погрешности. Во всех этих случаях наиболее распространена группа близких значений, но есть отклонения как в большую, так и в меньшую сторону.
Примеры решения задач
Рассмотрим несколько простых задач на применение правила 3 сигм.
Задача 1
Имеется выборка жителей богатого дома. Средняя зарплата жильцов составляет 150 000 рублей, среднеквадратичное отклонение равно 20 000 рублей. Определите, жители с какой зарплатой вряд ли могут жить в этом доме: А) 205 000 рублей; Б) 95 000; В) 230 000; Г) 87 000.
Решение
Чтобы решить данную задачу, необходимо определить, каковы верхние и нижние границы возможных зарплат в доме. Для этого воспользуемся правилом 3 сигм.
\(s_{нижн.}=\mu-3\sigma=150\;000-3\cdot20\;000=150\;000-60\;000=90\;000\)
\(s_{верх.}=\mu+3\sigma=150\;000+3\cdot20\;000=150\;000+60\;000=210\;000\)
Значения А, Б входят в диапазон \(\left[90\;000;\;210\;000\right]\). Значения В, Г не входят в него и, следовательно, являются искомыми грубыми ошибками.
Ответ: В, Г.
Задача 2
Завод выпускает партии по 100 цилиндрических деталей. Диаметр каждой детали — случайная величина, распределенная по нормальному закону. Математическое ожидание равно 65 мм, а среднее отклонение составляет 0,9 мм. Для упаковки партии используют коробки шириной 6600 мм. Детали кладут в один ряд. Если детали не поместятся в одну коробку, придется брать еще одну. Найдите вероятность, что понадобится только одна коробка.
Решение
Т. к. диаметр каждой детали распределен нормально, то и их общий диаметр также будет распределен нормально.
Чтобы все детали поместились в одну коробку, необходимо, чтобы отклонение диаметра всех деталей отклонялось от ожидаемого не более чем на 100 мм. Это следует из того, что математическое ожидание общего диаметра всех деталей равно \(65\cdot100=6500\). А ширина коробки составляет 6600 мм.
Для расчета воспользуемся формулами дисперсии и правилом 3 сигм, чтобы вычислить вероятность, что понадобится только одна коробка.
\(P\left|X-M(X)\right|<100\;\Rightarrow2\Phi\left[\frac{100}{100\sigma}\right]=2\Phi\left[1,111\right]=2\cdot0,3665=0,733\)
Ответ: 0,733
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так