Свойства прямой пропорциональности, область определения и значения
Прямая пропорциональность — базовые понятия
Пропорциональностью в алгебре называют зависимость между парой величин, при которой изменение одной из них приводит к изменению другой во столько же раз.
Пропорциональность бывает двух видов:
- прямая;
- обратная.
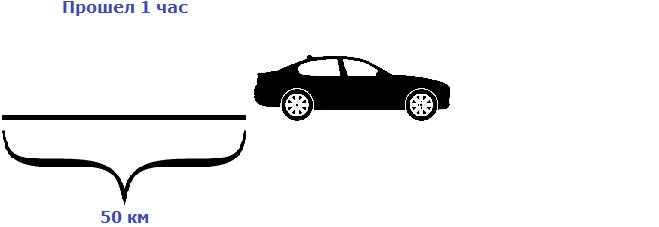
Предположим, что скорость движения автомобиля составляет 50 км/ч. По определению, скоростью является расстояние, преодолеваемое за единицу времени. В данном случае транспортное средство проезжает 50 километров в течение 1 часа.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если автомобиль движется в течение еще одного часа с такой же скоростью 50 км/ч, то он преодолеет расстояние в 100 км.
Согласно примеру, увеличение времени в 2 раза сопровождается увеличением пройденного расстояния во столько же раз, то есть в 2 раза. Величины времени и расстояния будут прямо пропорциональными. Они обладают взаимосвязью, которую называют прямой пропорциональностью.
Прямая пропорциональность – это взаимосвязь между двумя величинами, при которой увеличение одной из них приводит к увеличению другой во столько же раз и, наоборот, при уменьшении одной величины в какое-то число раз, другая величина уменьшается во столько же раз.
Предположим, что вначале водитель планировал проехать 100 км за 2 часа, но после того, как он преодолел 50 км, произошла остановка. В таком случае, уменьшая расстояние в 2 раза, получим, что время уменьшится тоже в 2 раза.
Особенностью прямо пропорциональных величин является стабильность их отношений. Таким образом, во время изменения значений прямо пропорциональных величин, их отношение остается постоянным. Рассмотренная ситуация характеризуется изменением расстояния с 50 км при значении времени в 1 час. Отношение расстояния ко времени равно 50 и определяется формулой:
\(\frac{50}{1}=50\)
После увеличения времени движения автомобиля в 2 раза, оно составит 2 часа. Таким образом, расстояние также увеличилось в 2 раза до 100 км. Отношение 100 км к 2 часам равно числу 50:
\(\frac{100}{2}=50\)
Число 50 представляет собой коэффициент прямой пропорциональности. Эта величина демонстрирует, какое расстояние соответствует одному часу движения. В условиях рассматриваемого примера данный коэффициент является скоростью движения автомобиля, исходя из ее определения.
С помощью прямо пропорциональных характеристик можно составлять пропорции. Например, записанные ранее отношения составляют пропорционально:
\(\frac{50}{1}=\frac{100}{2}\)
Представленное выражение читают таким образом: 50 км так относятся к 1 часу, как 100 км относятся к 2 часам.
Линейное уравнение относительно двух переменных x и y имеет такой вид:
ax + by + c = 0
\(a\neq 0\)
\(b\neq 0\)
Известно, что график записанного равенства является прямая линия, любая точка на которой имеет два числа в виде координат x и y, то есть абсциссы и ординаты. Каждая точка этой прямой соответствует заданному уравнению. Если выразить y через x, получим:
by = -ax - c
Принимая во внимание, что \(b\neq 0\), можно поделить на него две части выражения:
\(y=-\frac{a}{b}x-\frac{c}{b}\)
Сделать уравнение более удобным можно с помощью следующих обозначений:
\(-\frac{a}{b}=k\)
\(-\frac{c}{b}=m\)
Таким образом:
y = kx + m
Данным способом была выведена линейная функция y от x в общем виде. В этом случае были применены новые обозначения:
- x — в виде независимой переменной или аргумента;
- y — представляет собой зависимую переменную или функцию;
- k и m — являются параметрами, полностью и однозначно определяющими конкретную линейную функцию.
В том случае, когда m = 0, уравнение примет вид:
y = kx
Данная функция представляет собой прямую пропорциональность. Она определяется с помощью единственного параметра k.
Исследование функции прямой пропорциональности и ее график
Функция, которая обладает видом y = kx, где k — число (k≠0), является функцией прямой пропорциональности.
Число k представляет собой коэффициент пропорциональности. Переменная y пропорциональна переменной x. Прямая пропорциональность является частным случаем линейной функции
y = kx + m, если m=0
График прямой пропорциональности изображают в виде прямой, которая пересекает начало координат или точку O (0;0). Для того чтобы построить график прямой пропорциональности, требуется взять одну точку, вторая – будет точкой O.
Прямая пропорциональность характеризуется следующими свойствами:
- областью определения является множество действительных чисел: D(y): x∈(-∞;+∞) (или x∈R);
- областью значений является множество действительных чисел: D(y): y∈(-∞;+∞) (или y∈R);
- нуль функции (y=0) при x=0;
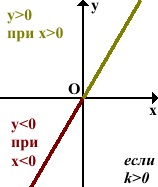
- если k>0, функция y = kx возрастает, а при k<0 — убывает;
Если k>0, график функции пересекает первую и третью координатные четверти. Функция будет обладать положительными значениями, если значения аргумента положительные:
y > 0 при x > 0.
Функция будет обладать отрицательными значениями, если значения аргумента отрицательные:
y < 0 при x < 0.
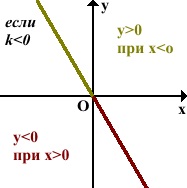
Если k < 0, то функция будет иметь график, проходящий через вторую и четвертую координатную четверть. Функция будет характеризоваться положительными значениями, если значения аргумента отрицательные:
y > 0 при x < 0.
Функция будет характеризоваться отрицательными значениями, если значения аргумента положительные:
y < 0 при x > 0.
Величина k представляет собой угловой коэффициент прямой y = kx. С другой стороны, k является тангенсом угла α, образованного прямой и положительным направлением оси Ох.
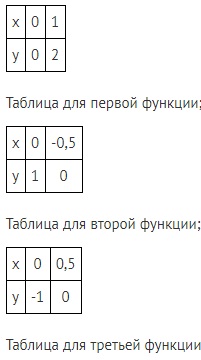
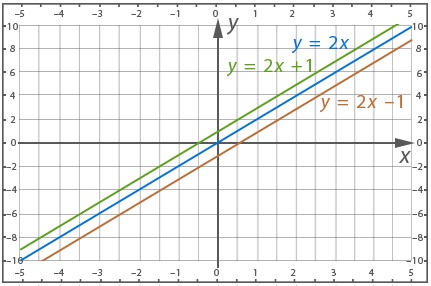
В качестве примера можно рассмотреть такие функции:
- y = 2x в виде прямой пропорциональности;
- y = 2x + 1 в виде линейной функции;
- y = 2x – 1 в виде линейной функции.
Можно построить график рассматриваемых функций. Каждая из них обладает коэффициентом k = 2. Для первой функции m = 0, для второй: m = 1, для третьей: m = -1. Данные величины вытекают из стандартной записи линейного уравнения:
y = kx + m
Необходимо представить данные в виде таблицы:
График примет такой вид:
Прямые, которые были построены, параллельны. Это объясняется равенством их угловых коэффициентов. Согласно теореме, если y = kx является графиком прямой пропорциональности, тогда график y = kx + m будет ему параллелен, так как коэффициентом k определяется угол наклона к оси x, и данный коэффициент y функций будет обладать равными значениями.
Примеры задач на прямую пропорциональность
Задача 1
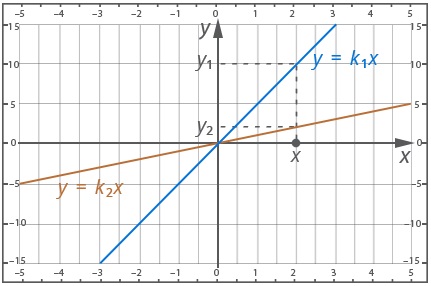
Требуется определить соотношение между угловыми коэффициентами, согласно графику:
Решение:
\(k_{1}=\frac{y_{1}}{x}\)
\(k_{2}=\frac{y_{2}}{x}\)
x = x;
\(y_{1}> y_{2}\)
Таким образом:
\(k_{1}>k_{2}\)
Ответ: \(k_{1}>k_{2}\)
Задача 2
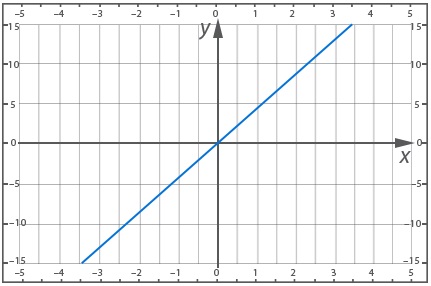
Требуется построить график прямой пропорциональности при том, что на данном графике есть точка с координатами (2;8).
Решение:
Построить прямую можно через пару точек. Первая будет обладать координатами (0;0), исходя из того, что любой график прямой пропорциональности пересекает точку (0;0). Вторая точка дана в условии задачи (2;8).
Задачу можно решить другим способом. Согласно координатам точки (2;8), получим:
x=2 и y=8
Данные выражения подходят для уравнения вида:
y = kx
Можно подставить известные значения и определить k:
8 = 2k
k = 4
Таким образом, уравнение примет вид:
y = 4x
С помощью данного уравнения можно построить график:
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так