Теорема о площади треугольника

Вывод формулы с доказательством

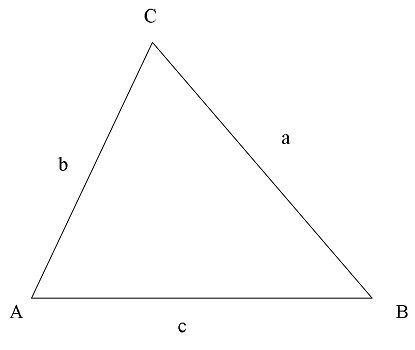
Для доказательства теоремы возьмем произвольный треугольник ABC.

Пусть BC = a, CA = b, S — площадь треугольника ABC.

Докажем, что \(S=\frac12ab\cdot\sin C\)

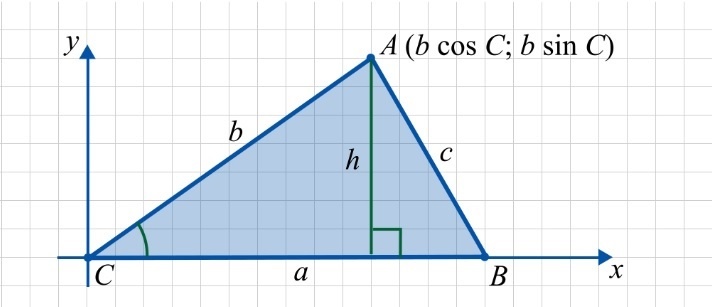
Введем координатную плоскость и впишем в нее треугольник ABC так, чтобы:

• точка C совпадала с началом координат;
• точка B лежала на положительной оси Cx;
• точка A находилась в верхней полуплоскости.

С учетом описанных условий вычисление площади треугольника можно произвести по формуле: 

\(S=\frac12ah\)

где h — высота треугольника. В данном случае h равна ординате точки A.

Получается, что \(h=b\cdot\sin C.\)

Это связано с тем, что \(\sin C\) равен отношению противолежащего катета (то есть h) к гипотенузе (то есть к b):

\(\sin C=\frac hb\)

Отсюда выражаем h и получаем:

\(h=b\cdot\sin C\)

Как следствие \(S=\frac12ab\cdot\sin C\), то есть вместо \(h\) подставляем \(b\cdot\sin C\). Теорема геометрии доказана.

Пример решения задачи

Задача

Дан прямоугольный треугольник \(ABC\), где \(AB = 3\), \(AC = 4\), \(\angle A=30\).

Найти площадь треугольника.

Решение

Для того чтобы найти площадь треугольника, воспользуемся ранее доказанной теоремой.

В формулу \(S=\frac12AB\cdot AC\cdot\sin A\) подставляем записанные выше исходные показатели и производим расчет.

\(S=\frac12\cdot3\cdot4\cdot\sin30^\circ=\frac12\cdot3\cdot4\cdot0,5=3\)

Ответ: \(\;S=3.\;\)