Формулировка прямой и обратной теоремы Менелая
Теорема Менелая и ее формулировка
Теорема Менелая в геометрии:
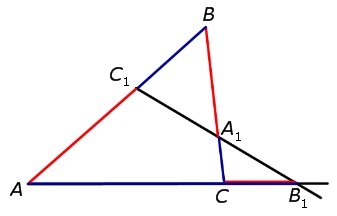
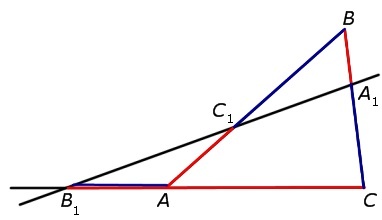
если на сторонах АВ и ВС треугольника АВС отмечены соответственно точки С1 и А1, а точка В1 расположена на продолжении стороны АС за точку С, то точки С1, А1 и В1 находятся на одной прямой тогда и только тогда, когда выполнено равенство: \(\frac{AC_{1}}{C_{1}B}\times \frac{BA_{1}}{A_{1}C}\times \frac{CB_{1}}{B_{1}A}=1\)
Схематично объяснение теоремы Менелая можно представить на рисунке:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Какие следствия из нее вытекают
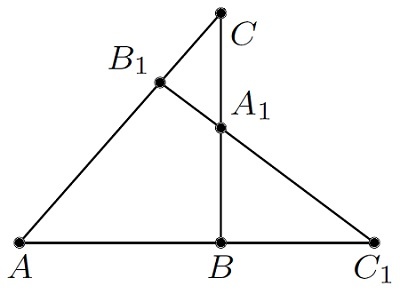
Необходимо отметить, что запоминание положения букв в данной теореме не является обязательным. Целесообразно применение простого алгоритма, с помощью которого можно представить запись всех дробей. Схема решения:
- начертить треугольник с секущей, обозначить положение вершин и точек какими-либо буквами;
- установить ручку или карандаш в точку, соответствующую любой вершине треугольника, обойти стороны геометрической фигуры, при этом обязательно пройти через точки пересечения с прямой;
- поделить соседние отрезки в таком прядке, который получился во время их обхода;
- в итоге получится три дроби, произведение которых соответствует единице.
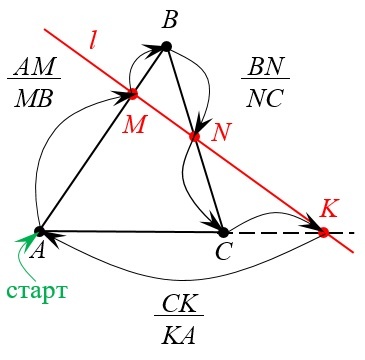
Алгоритм можно представить в виде чертежа:
С помощью такой простой схемы можно быстро восстановить запись формулы теоремы Менелая. Важные следствия, которые вытекают из данного утверждения
- В случае, когда прямая в пространстве пересекает вершину треугольника, теорема Менелая не работает.
- Если при начертании выбрать другую вершину в качестве стартовой точки или пойти в противоположную сторону, то уравнение сохранит справедливость, но изменится последовательность дробей.
Доказательство для прямой и обратной теоремы
Любое теоретическое утверждение нуждается в практическом подтверждении. В случае доказательства теоремы Менелая необходимо построить чертежи и использовать формулы, вытекающие из подобия треугольников или направленности векторов.
Через подобные треугольники
В том случае, когда расположение точек С1, А1 и В1 соответствует одной прямой, то справедливо равенство:
\(\frac{AC_{1}}{C_{1}B}\times \frac{BA_{1}}{A_{1}C}\times \frac{CB_{1}}{B_{1}A}=1\)
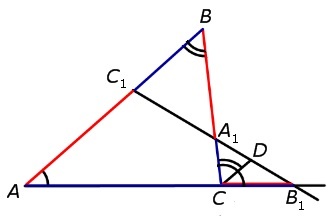
Следует начертить прямую, проходящую через точку С и параллельную прямой АВ. Точку, в которой эта прямая пересекает прямую С1В1, можно обозначить с помощью буквы D. Схематично такие действия представлены на рисунке:
Так как треугольники АС1В1 и СDВ1 подобны, то справедливо уравнение:
\(\frac{AC_{1}}{AB_{1}}=\frac{CD}{CB_{1}}\)
Исходя из того, что треугольники С1ВА1 и А1DС подобны, получаем равенство:
\(\frac{BA_{1}}{BC_{1}}=\frac{A_{1}C}{CD}\)
Далее необходимо перемножить полученные формулы:
\(\frac{AC_{1}}{AB_{1}}\times\frac{BA_{1}}{BC_{1}}=\frac{CD}{CB_{1}}\times\frac{A_{1}C}{CD} \Rightarrow\frac{AC_{1}}{AB_{1}}\times\frac{BA_{1}}{BC_{1}}=\frac{A_{1}C}{CB_{1}}\Rightarrow\frac{AC_{1}}{BC_{1}}\times\frac{BA_{1}}{AC_{1}}\times\frac {CB_{1}}{AB_{1}}=1\)
Данное равенство служит доказательством необходимости.
Для доказательства достаточности необходимо подтвердить, что в случае выполнения данного равенства:
\(\frac{AC_{1}}{C_{1}B}\times \frac{BA_{1}}{A_{1}C}\times \frac{CB_{1}}{B_{1}A}=1\)
точки С1, А1 и В1 будут расположены на одной прямой.
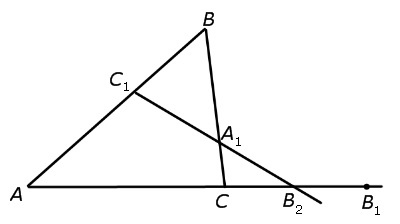
Целесообразно использовать при доказательстве методику «от противного». Для этого следует прочертить через точки С1 и А1 прямую и обозначить с помощью буквы В2 точку, в которой эта прямая пересекает прямую АС. Схематично такие действия можно представить на рисунке:
Исходя из того, что С1, А1 и В1 соответствуют одной прямой, то можно говорить о справедливости равенства:
\(\frac{AC_{1}}{C_{1}B}\times \frac{BA_{1}}{A_{1}C}\times \frac{CB_{2}}{B_{2}A}=1\)
Также выполняется условие следующего уравнения:
\(\frac{AC_{1}}{C_{1}B}\times \frac{BA_{1}}{A_{1}C}\times \frac{CB_{1}}{B_{1}A}=1\)
Далее следует разделить полученное уравнение на первоначальную формулу:
\(\frac{CB_{2}}{B_{2}A}\times \frac{B_{1}A}{CB_{1}}=1\)
Исходя из данного равенства, получим:
\(\frac{CB_{2}}{B_{2}A}\times \frac{CB_{1}}{B_{1}A}\)
Согласно свойствам производных пропорций, можно сделать вывод о совпадении точек В1 и В2. В результате доказательство достаточности получено. Теорему Менелая можно считать полностью доказанной.
В случае некоторого изменения формулы теоремы Менелая при выборе точки В1 на продолжении стороны АС за точку А, ход доказательства теоремы сохранится прежним.
Рисунок будет иметь такой вид:
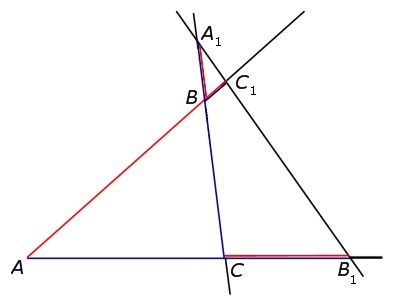
Доказательство теоремы Менелая 2 начинают с построения рисунка. Если на продолжениях сторон АВ, ВС и АС, которыми обладает треугольник АВС, отметить точки С1, А1 и В1 соответственно, то точки С1, А1 и В1 будут принадлежать одной прямой только в том случае, когда выполнимо равенство:
\(\frac{AC_{1}}{C_{1}B}\times \frac{BA_{1}}{A_{1}C}\times \frac{CB_{1}}{B_{1}A}=1\)
Процесс подтверждения теоремы Менелая 2 аналогичен доказательству теоремы Менелая 1.
Через векторы
Отношением \(\frac{\vec{a}}{\vec{b}}\) направленных отрезков \(\vec{a}\) и \(\vec{b}\) принадлежащих одной прямой, либо расположенных на параллельных прямых, называют число k такое, при котором справедливо равенство:
\(\vec{a}=k\times \vec{b}\)
Согласно определению k>0, в случае, когда вектора ориентированы в одном направлении, и k<0, когда вектора противоположны друг другу.
Предположим, что прямые ВС, СА и АВ, содержащие стороны треугольника АВС, включают точки А1, В1 и С1. Данные точки расположены на одной прямой только в том случае, когда выполняется равенство:
\(\frac{\vec{AB_{1}}}{\vec{B_{1}C}}\times \frac{\vec{CA_{1}}}{\vec{A_{1}B}}\times \frac{\vec{BC_{1}}}{C_{1}A}=1\)
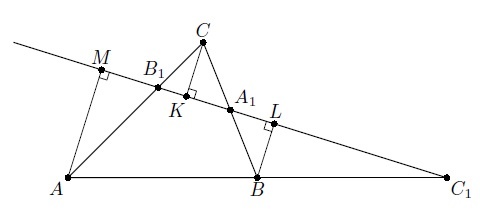
Необходимо подтвердить, что в случае расположения точек А1, В1 и С1 на одной прямой, равенство будет справедливо. Требуется построить перпендикуляры АМ, СК и BL, выходящие из вершин треугольника к рассматриваемой прямой. Треугольники АВ1М и СВ1К подобны, поэтому:
\(\frac{AB_{1}}{B_{1}C}=\frac{AM}{CK}\)
\(\frac{CA_{1}}{A_{1}B}=\frac{CK}{BL}\)
\(\frac{BC_{1}}{C_{1}A}=\frac{BL}{AM}\)
Из полученных формул можно вывести уравнение:
\(\frac{AB_{1}}{{B_{1}C}}\times \frac{{CA_{1}}}{A_{1}B}\times \frac{BC_{1}}{C_{1}A}=1\)
Важно отметить, что допустимо два варианта:
- пара точек будет расположена на сторонах треугольника и одна находиться на продолжении стороны;
- все три точки размещены на продолжениях сторон геометрической фигуры.
В первом варианте только одно отношение направленных отрезков будет соответствовать отрицательному значению, а во втором – все три.
Таким образом:
\(\frac{\vec{AB_{1}}}{\vec{B_{1}C}}\times \frac{\vec{CA_{1}}}{\vec{A_{1}B}}\times \frac{\vec{BC_{1}}}{C_{1}A}=-1\)
Теорема считается доказанной. Можно предположить, что равенство справедливо, но точки А1, В1 и С1 не находятся на одной прямой. Тогда прямая А1В1 будет пересекать прямую АВ, точка С2 будет являться точкой пересечения. В таком случае можно записать уравнение:
\(\frac{\vec{AB_{1}}}{\vec{B_{1}C}}\times \frac{\vec{CA_{1}}}{\vec{A_{1}B}}\times \frac{\vec{BC_{2}}}{C_{2}A}=-1\)
Заметим, что выполняется равенство:
\(\frac{\vec{AB_{1}}}{\vec{B_{1}C}}\times \frac{\vec{CA_{1}}}{\vec{A_{1}B}}\times \frac{\vec{BC_{1}}}{C_{1}A}=-1\)
В таком случае:
\(\vec{BC_{2}}{C_{2}A}={\vec{BC_{1}}}{C_{1}A}\)
Таким образом, точки С1 и С2 будут совпадать, что и требовалось доказать.
Примеры решения задач
Задача 1
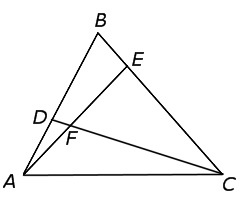
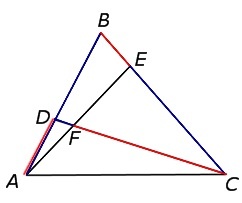
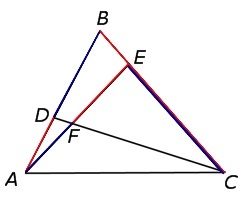
Треугольник АВС обладает сторонами АВ и ВС, на которых отмечены точки D и Е соответственно. Также справедливо равенство:
\(AD=\frac{3}{8}AB\)
\(BE=\frac{1}{5}BC\)
Отрезки АЕ и CD пересекают друг друга в точке F, как показано на рисунке. Требуется определить отношение отрезков АЕ и CD, поделенных точкой F.
Решение
Следует использовать теорему Менелая для треугольника BCD.
В таком случае:
\(\frac{BE}{EC}\times \frac{CF}{FD}\times \frac{DA}{AB}=1\Rightarrow \frac{1}{4}\times \frac{CF}{FD}\times \frac{3}{8}=1\Rightarrow \frac{CF}{FD}=\frac{32}{3}\)
Необходимо применить теорему Менелая для треугольника АВЕ.
\(\frac{AD}{DB}\times \frac{BC}{CE}\times \frac{EF}{FA}=1\Rightarrow \frac{3}{5}\times \frac{5}{4}\times \frac{EF}{FA}=1\Rightarrow \frac{EF}{FA}=\frac{4}{3}\)
Ответ: \( \frac{CF}{FD}=\frac{32}{3}\), \( \frac{EF}{FA}=\frac{4}{3}\)
Задача 2
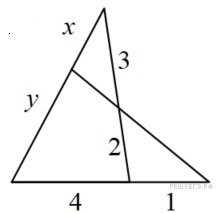
На рисунке изображен треугольник. Исходя из его характеристик, необходимо определить отношение \(\frac{x}{y}\)
Согласно теореме Менелая, получим равенство:
\(\frac{x}{y}\times \frac{5}{1}\times \frac{2}{3}=1\)
Таким образом:
\( \frac{x}{y}=\frac{3}{10}\)
Ответ: \( \frac{3}{10}\)
Задача 3
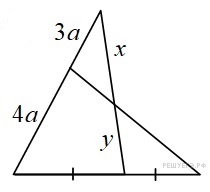
На рисунке изображена геометрическая фигура в виде треугольника. Исходя из данных на схеме, требуется рассчитать отношение \(\frac{x}{y}\)
Решение
Руководствуясь теоремой Менелая, запишем уравнение:
\(\frac{x}{y}\times \frac{1}{2}\times \frac{4a}{3a}=1\)
Таким образом:
\(\frac{x}{y}=\frac{3}{2}\)
Ответ: \( \frac{3}{2}\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так