Как найти точки минимума и максимума функции

Минимум и максимум функции

Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом: 

• \(y_{min}, y_{max}\) — минимум, максимум функции или экстремумы;
• \(x_{min}, x_{max}\) — точки минимума, максимума функции;
• \(y_{наиб}, y_{наим}\) — наибольшее (максимальное), наименьшее (минимальное) значение функции.

Точка минимума, минимум функции

Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.

Точка максимума, максимум функции

Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.

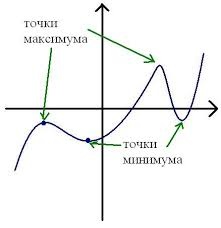
Точки максимума и минимума на графике:

Исследование функций на экстремумы

Алгоритм нахождения экстремумов с помощью производной:

1. Найти область определения функции — D(y).

2. Определить производную — f '(x).

3. Определить стационарные точки y = f(x), т.е. те, которые принадлежат D(y), f '(x) в них обращается в ноль, отыскать критические точки, в которых производной не существует (пример: \(f^,(x)=\frac1{2\sqrt x}\), производной не существует при x = 0).

4. Исследовать характер изменения функции f (x) и знак f '(x) в промежутках, на которые найденные критические точки делят область определения (при отрицательном знаке производной функция убывает, при положительном — возрастает).

5. Относительно каждой критической точки определить, является ли она точкой максимума, минимума  (возрастание меняется на убывание — точка максимума, убывание на возрастание — минимума) или не является точкой экстремума (то есть, меняется ли знак производной при переходе через исследуемую точку).

6. Вычислить значения функции в точках экстремума.

Примеры задач

Задача 1

Исследовать на экстремумы функцию \(f(x)=x^3-3x^2.\)

Решение задачи по алгоритму:

1) \(D(y): x\in(-\infty;+\infty)\), т.е. x — любое число.

2) Производная: \(f'(x)=3x^2-6x\) .

3) Из пункта 1 следует, что критических точек нет. Найдем стационарные:

Приравниваем f '(x) к 0, решаем квадратное уравнение \(3x^2-6x=0\), получаем \(x_1=0\),\(\;x_2=2.\)

4) Отметим на горизонтальной оси координат точки 0 и 2. Подставим любое x из интервала \((-\infty;0)\) в f'(x), например, пусть x = -1, тогда \(f'(x)=3{(-1)}^2-6(-1)=3+6=9\). Получаем f '(x)>0, значит на исследуемом интервале f(x) возрастает. Аналогично рассмотрим оставшиеся интервалы. Итого, на отрезке (0;2) производная отрицательна, функция убывает, а на интервале \((2;+\infty)\) производная положительна, возрастает. Из этого следует, что x=0 - точка максимума, а x=2 - минимума.

5) Найдем значение экстремумов функции.

\(f(0)=0-3\times0=0\)

\(f(2)=2^3-3\times2^2=8-12=-4\)

Ответ: \(x_{min}=2,\;y_{min}=-4;\;x_{max}=0,\;y_{max}=0\) или (0;0) - минимум функции, (2;-4) - максимум.

Задача 2

Найти промежутки монотонности функции \(f(x)=\frac x{x^2-4}\).

1) \(D(y): x\in\mathbb{R},\;\)кроме\(\;\pm2\)

2) \(f'(x)=\frac{1(x^2-4)-x\times2x}{{(x^2-4)}^2}=-\frac{x^2+4}{{(x^2-4)}^2}\)

3) Итак, как выяснилось в пункте 1, критические точки 2 и -2. Если мы приравняем f '(x) к 0, чтобы найти стационарные точки, то увидим, что уравнение не будет иметь корней. Значит, стационарных точек нет. Из этого следует, что функция монотонна на всей области определения. Проверим, возрастает она или убывает. Для этого решаем неравенство \(-\frac{x^2+4}{{(x^2-4)}^2}\leq0\) и получим, что неравенство верно при любом x, значит функция убывает.

Не забываем, что в ответе, указывая промежуток, обязательно нужно исключить критические точки -2 и 2 т.к. в них функция не определена.

Ответ: f(x) убывает на промежутке \((-\infty;-2)\cup(-2;2)\cup(2;+\infty)\).

Задача 3

Докажите, что функция \(f(x)=x^5+2x^3-4\) возрастает на всех числовой прямой.

1) \(D(y): x\in\mathbb{R}\), значит критических точек нет.

2) \(f'(x)=5x^4+6x\)

3) Приравняем f'(x) к 0 и найдем корень: x = 0. Отметим 0 на числовой прямой и определим знак производной на промежутках \((-\infty;0)\) и \((0;+\infty)\). Получим, что производная положительна на обоих промежутках, следовательно функция возрастает на всей числовой прямой.

Утверждение доказано