Точки экстремума функции

Что такое точки экстремума

Источник: brilliant.org

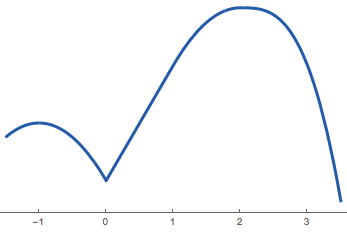
Эта функция имеет абсолютный экстремум при x=2 и локальный экстремум при x=-1.

Локальный максимум — это точка(c,f(c)) на графике функции f(x) такая, что f(c)≥f(x) для всех x и нескольких интервалов вокруг c. Аналогично, локальный минимум — это точка (c,f(c)) такая, что f(c)≤f(x) для всех x и нескольких интервалов вокруг c. Локальный максимум не обязательно должен находиться там, где функция принимает наибольшее возможное значение. Он просто является наибольшим в некоторой области вокруг себя.

Необходимое условие экстремума функции

Необходимые и достаточные условия экстремумов функции позволяют определить, когда точка является экстремумом и является ли она максимумом или минимумом.

Необходимое условие экстремума (тест первой производной): Если функция f(x) имеет локальный экстремум в точке x=c, тогда производная f′(c) должна быть равна нулю или не определена в этой точке: f′(c)=0 или f(c) не определена.
Это условие указывает на то, что в точке экстремума наклон касательной к кривой либо горизонтален (нулевой наклон), либо не определен.

Достаточное условие экстремума функции

Для определения наличия локального экстремума в точке x=c является максимумом или минимумом, можно воспользоваться тестом на вторую производную. Если f′(c)=0 (из необходимого условия), тогда:

1. Если f′′c>0, то это локальный минимум.
2. Если f′′c<0, то это локальный максимум.
3. Если f′′c=0, то тест не дает результата.

Тест на вторую производную проверяет вогнутость функции в точке экстремума. Положительная вторая производная указывает на локальный минимум (кривая вогнута вверх), а отрицательная вторая производная — на локальный максимум (кривая вогнута вниз).

Как найти, формулы

Поиск локальных экстремумов путем проверки критических точек функции:

1. Найдите критические точки функции f(x), приравнивая первую производную к нулю.
2. Используя интервалы между критическими точками, оцените, положительна или отрицательна функция f'(x) в этом интервале. Это можно сделать, выбрав значения x в интервале и подставить в f'(x). Важен только знак ответа, а не само значение. Например, если f'(1) = -3, то нам достаточно извлечь, что производная отрицательна в x=1.
3. Определите критические точки, в которых производная меняет знак, как локальные экстремумы. Обязательно исключите все значения x, не входящие в область f.

• Переход от отрицательного к положительному означает, что f(x) имеет локальный минимум.
• Переход от положительного к отрицательному означает, что f(x) имеет локальный максимум.

Примеры решения задач

Решение:

1. Вычислим производную функции $f(x)$: f′(x)=2x−4

2. Поставим производную равной нулю и решим уравнение: $2x-4=0;$ $2x=4;$ $x=2.$

   Критической точкой является $x=2$.

3. Вычислим вторую производную: f′′(x)=2. Значение второй производной f′′(x) всегда равно 2, что является положительным числом. Это означает, что у нас есть точка минимума в критической точке $x=2$.

Таким образом, точка экстремума функции f(x)=x2−4x+5 — это точка минимума, и она находится в $x=2$, а значение функции в этой точке можно найти, подставив $x=2$ в исходную функцию:

f(2)=22−4⋅2+5=4−8+5=1.

Итак, точка экстремума функции $f(x)$ равна (2, 1).

Дифференцируя f(x) относительно x дает f′(x)=3x²-4kx-4k. Для функции f(x) не имеет экстремумов, должно быть верно уравнение f′(x)=0 имеет либо повторный корень, либо нереальные, комплексные корни. Это эквивалентно утверждению, что дискриминант уравнения f′(x)=3x²-4kx-4k=0 должна быть неположительной:

D/4 = (-2k)²-3⋅(-4K) = 4k(k+3)≤0. Следовательно, диапазон k такой, что f(x) не имеет экстремумов, является -3≤k≤0.

Так как x → ± ∞, f(x) → ∞. Следовательно, функция не имеет наибольшего значения. Однако, поскольку x²+1≥1 для всех действительных чисел x и x²+1=1, когда x=0, функция имеет наименьшее значение 1, когда x=0. 1 является абсолютным минимумом функции f(x)=x²+1 и возникает при x=0. Также f(x)=x2+1 не имеет абсолютного максимума.

Источник: courses.lumenlearning.com

График функции f(x) = x2 + 1 построен, и видно, что ее минимум, равный 1, находится при x = 0.
Данная функция имеет абсолютный минимум, равный 1, в точке x=0. Функция не имеет абсолютного максимума.