О тригонометрических неравенствах: понятие, типы и особенности решения
Что такое тригонометрические неравенства
Тригонометрические неравенства — неравенства, в которых переменные находятся только под знаком тригонометрической функции.
Тригонометрические функции обозначаются как:
- sin α;
- cos α;
- tg α;
- ctg α.
При доказательстве тригонометрических неравенств применяют общие приемы доказательства алгебраических неравенств.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
При этом в тригонометрии спектр применяемых математических методов богаче.
К ним относятся:
- метод от обратного;
- аналитико-синтетический метод;
- методы математического анализа;
- метод математической индукции;
- элементы геометрии;
- векторная алгебра;
- графический метод.
Виды тригонометрических неравенств
Неравенства в тригонометрии подразделяются на два вида:
- простейшие;
- сложные.
По однородности они делятся на два типа:
- однородные;
- неоднородные.
В однородных неравенствах у всех слагаемых степень одинакова по сумме.
Примеры таких неравенств:
- \(\left(x-2\right)^4-8x^2{(x-2)}^2+7x^4<0{(x-2)}^4-10x^2{(x-1)}^2+9x^4<0\);
- \(6^x-2\cdot4^x\cdot5^x+25^x\geq0;\)
- \(a\;\sin^2\left(x\right)+b\;\cos\left(x\right)\sin\left(x\right)+c\;\cos^2\left(x\right)\geq0.\)
В неоднородных — степени слагаемых будут отличаться друг от друга.
Простейшие
Простейшие тригонометрические неравенства имеют вид:
sin х < m, sin x > m, cos x < m, cos x > m, tg x < т, tg x > m, ctg >m; ctg < m,
где m — заданное число.
Сложные
В сложных тригонометрических неравенствах аргумент функции неравенства имеет вид целого выражения с неизвестной, а не просто переменной.
Они бывают:
- дробные;
- двойные;
- тройные;
\(\sin\left(\frac x2+\frac\pi3\right)<\frac{\sqrt2}2\ \)
\(sin 3x - sin x > 0; \)
\(cos x - 5x + 2 > 0.\)
Методы решения тригонометрических неравенств
Общие сведения по решению тригонометрических неравенств
При решении тригонометрических неравенств используют свойство монотонности тригонометрических функций и промежутки их знакопостоянства.
Монотонность характерна как для убывающих, так и для возрастающих функций. Она означает, что в определенном промежутке большему по значению аргумента будет соответствовать большее или меньшее значение функции в зависимости от возрастания или убывания функции, соответственно.
О промежутках знакопостоянства говорят, когда множеству значений аргумента соответствуют только положительные или только отрицательные значения функции.
Чтобы решить простейшее тригонометрическое неравенство, необходимо найти множество всех значений аргумента, которые обращают данное неравенство в верное числовое неравенство.
Важные моменты в решении простейших тригонометрических неравенств:
- для sin x:
sin x = 0, если \(\mathrm x=\mathrm{πR}, \ R\in Z;\)
sin x = -1, если \(x=-\frac\pi R+2\pi R\,, \ R\in Z;\)
sin x = 1, если \(x=\frac\pi2+2\pi R, \ R\in Z;\)
sin x > 0, если \(2\pi R<x<\pi+2\pi R, \ R\in Z;\)
sin x < 0, если \(-\pi+2\pi R<x<2\pi R, \ R\in Z.\)
для cos x:
cos x = 0, если \(x=\frac\pi2+\pi R,\ R\in Z;\)
cos x = -1, если \\(x=\pi+2\pi R, \ R\in Z;\)
cos x = 1, если \(x=2\pi R, \ R\in Z;\)
cos x > 0, если \(2\pi R-\frac\pi2<x<\frac\pi2+2\pi R, \ R\in Z;\)
cos x < 0, если \(2\pi R+\frac\pi2<x<\frac32\pi+2\pi R, \ R\in Z.\)
- для tg x:
tg x > 0, если \(\pi R<x<\frac\pi2+\pi R, \ R\in Z;\)
tg x < 0, если \(\pi R-\frac\pi2<x<\pi R, \ R\in Z;\)
тангенс не существует, если \(x=\frac\pi2+\pi R, \ R\in Z.\)
Нестандартные способы решения тригонометрических неравенств включают в себя несколько методик:
- Графический метод.
- Метод постановки.
- Метод интервалов.
- Метод секторов.
- Метод концентрических окружностей для систем тригонометрических неравенств.
Для решения простейших тригонометрических неравенств применяют графический способ решения и решение с помощью числовой окружности.
Решение тригонометрических неравенств с помощью единичной окружности
Решите неравенство: sin x > ½.
Решение:
Построим единичную окружность. Построим на ней дуги AC и \(AC_1\). Их синус должен быть равен ½.
Из окружности видно, что все дуги, начинающиеся в точке А и заканчивающиеся в любой внутренней точке дуги \(CBC_1\), удовлетворяют данному неравенству.
Соответственно:
\(\frac\pi6<x<\frac{5\pi}6.\)
Чтобы получить все решения данного неравенства, прибавим к концам этого промежутка 2πR.
Ответ: \(\frac\pi6+2\pi R<x<\frac{5\pi}6+2\pi R, \ R\in Z.\)
Решите неравенство: cos 3x > ½.
Решение:
Обозначим 3х через α.
Неравенство примет вид:
\(\cos\left(\alpha\right)\geq-\frac12.\)
Построим окружность.
Этому неравенству удовлетворяют все точки \[P_\alpha\] единичной окружности, абсциссы которых больше или равны -1/2.
На окружности видно, что эти точки дуги лежат на прямой \(х=-1/2\) или правее ее.
Выделенная на рисунке дуга представляет собой множество всех точек, удовлетворяющих данному неравенству. Концы этой дуги входят в искомое множество. Их абсциссы равны -1/2, значит, удовлетворяют неравенству.
Соответственно:
\(-\frac{2\pi}3\leq\alpha\leq\frac{2\pi}3.\)
Учитывая периодичность косинуса, запишем решения для неравенства
\(\cos\left(\alpha\right)\geq-\frac12:\)
\(-\frac{2\pi}3+2\pi R\leq\alpha\leq\frac{2\pi}3+2\pi R, \ R\in Z.\)
Вернемся снова к переменной х, получим искомый ответ:
\(-\frac{2\pi}3+2\pi R\leq3x\leq\frac{2\pi}3+2\pi R,\;R\in Z;\)
\(-\frac{2\pi}9+\frac{2\pi R}3\leq x\leq\frac{2\pi}9+\frac{2\pi R}3,\;R\in Z.\)
Решите неравенство: tg 2x > 1.
Решение:
Обозначим 2х через α.
Неравенство примет вид:
\(tg α > 1.\)
Построим окружность и проведем касательную к окружности в точке (1; 0). Эта линия является тангенсом.
Так как α является решением неравенства tg α ≥ 1, то ордината точки \(T_\alpha\) линии тангенсов tg α должна быть равна или больше 1. Луч АТ имеет все эти точки.
Точки \(P_\alpha\) окружности, соответствующие точкам \( P_\alpha\), образуют дугу.
Для ее точек выполняется неравенство \(\frac\pi4\leq\alpha<\frac\pi2.\)
Прибавим к этому промежутку период тангенса и получим решение неравенства \(T_\alpha\geq1:\)
\(\pi R+\frac\pi4\leq\alpha<\frac\pi2+\pi , \ R\in Z.\)
Так как \(α=2х\), получим ответ:
\(\frac{\pi R}2+\frac\pi8\leq x<\frac\pi4+\frac{\pi R}2, \ R\in Z.\)
Графическое решение тригонометрических неравенств
Для решения простейших тригонометрических неравенств с помощью графического метода решения строят график тригонометрической функции (sin x, cos x и т. д.) и прямую у=а. Затем выделяют промежутки с помощью построенных графиков. Эти промежутки являются решением неравенства.
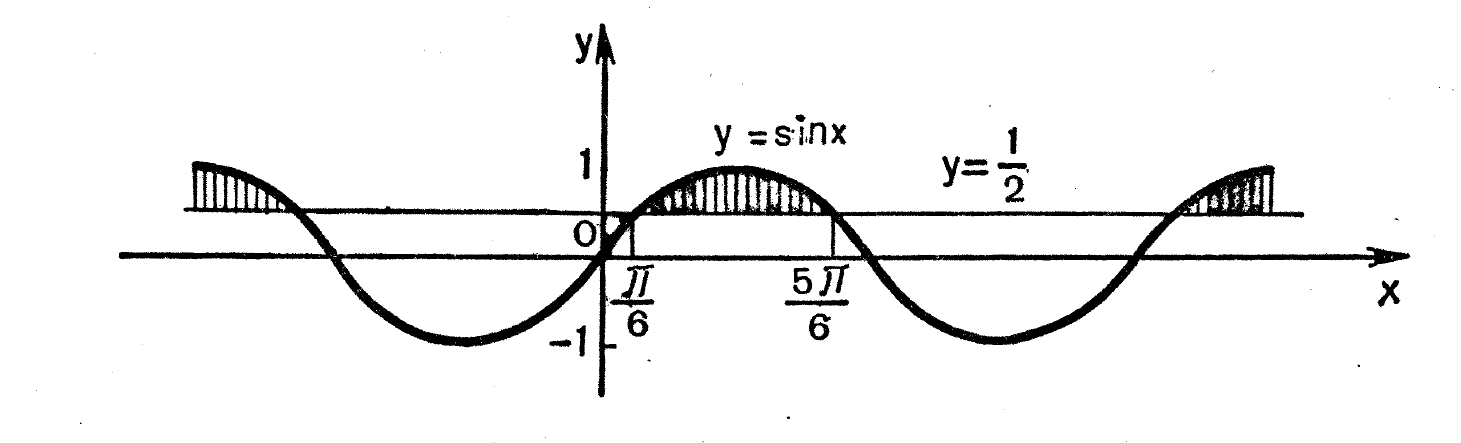
Решите неравенство: sin x > ½.
Решение:
Построим графики функций \(y=sin\) \(x\) и \(y=1/2.\)
Из графика видно, что прямая у=1/2 пресекает синусоиду в бесконечном числе точек.
На нем выделены несколько значений аргументов, которые удовлетворяют данному неравенству: \(\frac\pi6, \frac{5\pi}6.\)
Учитывая периодичность синуса, запишем окончательный ответ:
\(\frac\pi6+2\pi R<x<\frac{5\pi}6+2\pi R,\) \(R\in Z.\)
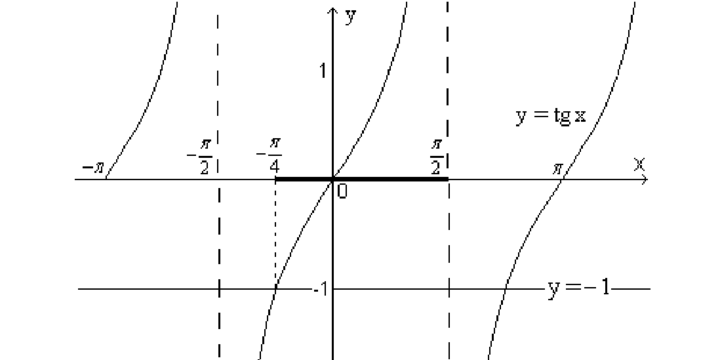
Решите неравенство: tg x ≥ -1.
Решение:
Построим графики функций \(y = tg\) \(x \) и \(y = -1.\)
Из графика видно, что одним из промежутков, который удовлетворяет неравенств, является:
\(\left[-\frac\pi4;\;\frac\pi2\right].\)
Учтем периодичность тангенса и получим:
\(x\in\left[-\frac\pi4+k\pi;\;\frac\pi2+k\pi\right],\;k\in Z.\)
Получим ответ:
\(\left[-\frac\pi4+k\pi;\;\frac\pi2+k\pi\right],\;k\in Z.\)
Решение тригонометрических неравенств методом интервалов
Решите неравенство: \(6\sin^2\left(x\right)-5\sin\left(x\right)+1\geq0.\)
Решение:
Введем новую переменную:
\(y = sin x.\)
Тогда данное неравенство можно записать в другом виде:
\(6y^2-5y+1\geq0.\)
Это неравенство представляет собой квадратное уравнение с корнями:
\(y_1=\frac12 \ и \ y_2=\frac13.\)
Получим из данного трехчлена линейные множители, используя формулу:
\(ax^2+bx+c=a(x-x_1)(x-x_2).\)
Получим:
\(6y^2+5y+1=6(y-\frac13)(y-\frac12)\geq0.\) (1)
Используем метод интервалов для его решения.
Объединим промежутки \(y\geq\frac12\) и \(y\leq\frac13.\)
Тогда получим, что
\(\sin\left(x\right)\leq\frac13\) и \(\sin\left(x\right)\geqslant\frac12.\) (2)
Теперь для решения полученных неравенств применим алгоритм решения по методу единичной окружности.
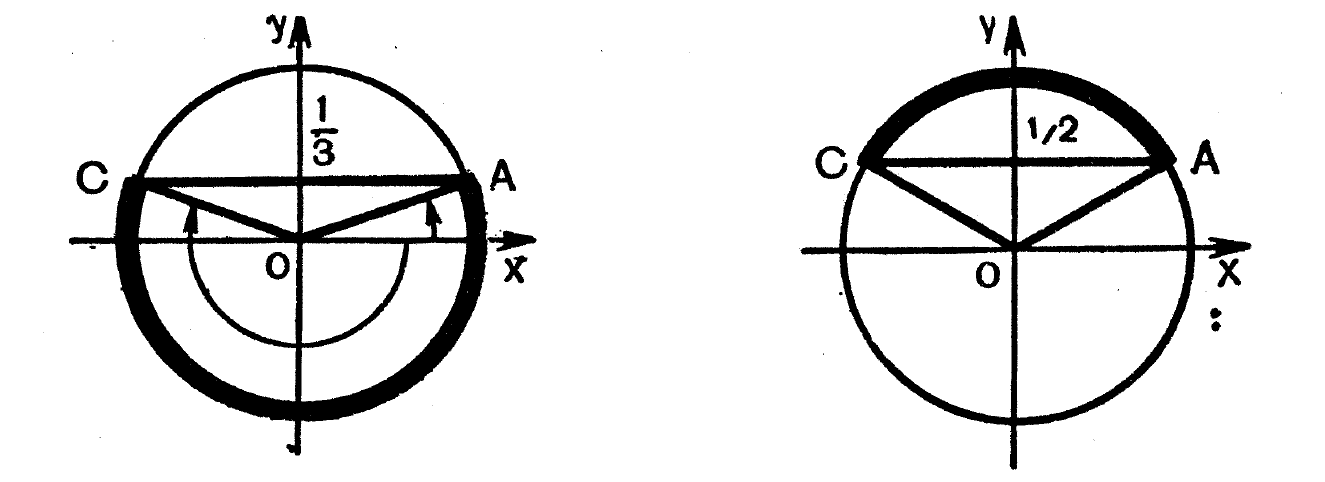
Решая неравенство (1), на построенной слева окружности видим, что ему удовлетворяют такие значения х:
\(-\pi-arc\sin\frac13\leq x\leq arc\sin\frac13\). (3)
Для получения всех решений неравенства к полученному промежутку добавим \(2\pi R.\)
Окончательно имеем:
\(-\pi-arc\sin\;\frac13+2\pi R\leq x\leq arc\sin\;\frac13+2\pi R,\;R\in Z\). (4)
Для решения неравенства (2) так же построим окружность и увидим, что ему удовлетворяют значения х:
\(\frac\pi6+2\pi R\leq x\leq\frac{5\pi}6+2\pi R,\;R\in Z.\) (5)
Значения х, удовлетворяющие неравенствам (4) и (5) являются решением данного неравенства.
Задача 2
Решите неравенство: \(\frac{15}{\cos\;x\;+1}<11\;-\;2\;\cos\;x.\)
Решение:
Введем новую переменную: \(у = cos x.\)
Неравенство примет вид:
\(\frac{15}{y\;+1}<11\;-\;2y.\)
После преобразований получим:
\(\frac{2(y-4)\left(y-{\displaystyle\frac12}\right)}{y+1}<0.\)
Используем метод интервалов.
Решение неравенства:
\(y<-1;\;\frac12<y<4.\)
Неравенство \(\cos\;x<-1\) решения не имеет.
Так как \(-1\leqslant\cos\;x\leqslant\), то неравенство \(\frac12<\cos\;x<4\) надо заменить другим неравенством:
\(\frac12<\cos\;x\leq1.\)
Его решением будет:
\(2\pi R-\frac\pi3<x<\frac\pi3+2\pi R,\;R\in Z\ \)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так