Основные тригонометрические формулы

Описание тригонометрических формул

Термин «тригонометрия» дословно означает «измерение треугольников». Его ввел в употребление немецкий математик и богослов Варфоломей Питиск, автор учебника по тригонометрии и тригонометрических таблиц. Но саму тригонометрию — ее основные функции и их таблицы — придумали еще до нашей эры, в Древнем Вавилоне.

Основная функция

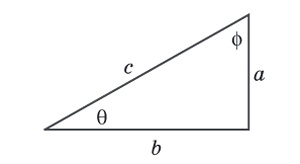
Чтобы производить косвенные измерения расстояний между звездами и их расположения относительно друг друга, небо представляли в виде сферы. Тогда задача сводилась к анализу треугольника, одни элементы которого можно выразить через другие. Исторически для измерения брали прямоугольные треугольники, поэтому основные функции относятся к ним. Это синус, косинус и тангенс.

\(\sin\left(\theta\right)\;=\;\frac ас\)

\(\cos\left(\theta\right)\;=\;\frac bс\)

\(\tan\left(\theta\right)\;=\;\frac ab\;=\;\frac{\sin\left(\theta\right)}{\cos\left(\theta\right)}\)

Тригонометрические тождества

С учетом этого тождества можно вывести следующие соотношения:

\(1\;+\;\tan^2\left(\alpha\right)\;=\;\frac1{\cos^2\left(\alpha\right)}\;=\;sec^2(\alpha)\)

\(1\;+\;ctn^2\left(\alpha\right)\;=\;\frac1{\sin^2\left(\alpha\right)}\;=\;csec^2(\alpha)\)

\(\tan^{}\left(\alpha\right)\;\times\;ctn\left(\alpha\right)\;=\;1\)

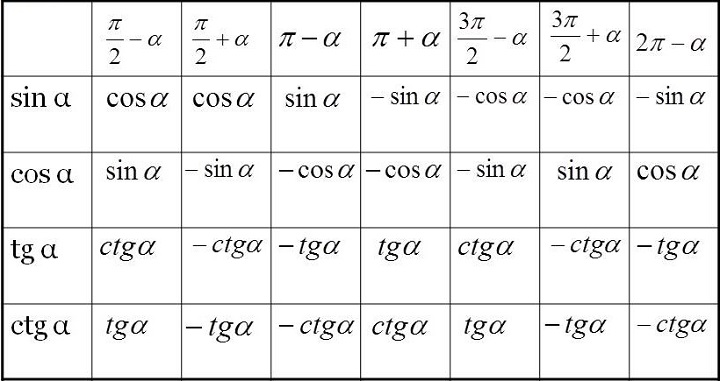
Формулы приведения

Что позволяют формулы

С их помощью значение тригонометрической функции любого угла можно привести к значению как той же, так и другой функции острого угла. Это позволяет, имея тупой угол, перейти к работе с острым, что намного удобнее для решения задач.

Часто в таблицах приводятся формулы только для синуса и косинуса, из которых легко получить формулы для тангенса и котангенса. При необходимости их можно переписать, заменяя радианы на градусы. Для этого нужно подставить вместо числа пи 180 градусов.

Формулы приведения не нужно заучивать наизусть. Достаточно запомнить закономерность, известную как мнемоническое правило:

1. Представить аргумент исходной функции в виде:

   \(\pm\;\alpha\;+\;2\pi\;\times\;z,\;\frac{\mathrm\pi}2\;\pm\;\alpha\;+\;2\pi\;\times\;z,\;\pi\;\pm\;\alpha\;+\;2\pi\;\times\;z,\;\frac{3\mathrm\pi}2\;\pm\;\alpha\;+\;2\pi\;\times\;z,\;\)

2. Определить знак исходной функции — тот же знак будет иметь функция в правой части формулы приведения.

3. Сохранить название исходной функции для углов: 

   \( \pm\;\alpha\;+\;2\pi\;\times\;z,\;\pi\;\pm\;\alpha\;+\;2\pi\;\times\;z\)

4. Заменить название исходной функции на название кофункции (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангес) для углов:

   \(\frac{\mathrm\pi}2\;\pm\;\alpha\;+\;2\pi\;\times\;z,\;\frac{3\mathrm\pi}2\;\pm\;\alpha\;+\;2\pi\;\times\;z\)

Следствием чего являются

Формулы приведения следуют из свойств тригонометрических функций:

• периодичности;
• симметричности;
• сдвига на данный угол.

Формулы сложения

Эти формулы обычно группируют попарно, используя знаки «плюс-минус» и «минус-плюс».

\(\sin\left(\alpha\pm\beta\right)\;=\;\sin\left(\alpha\right)\cos\left(\beta\right)\;\pm\;\cos\left(\alpha\right)\sin\left(\beta\right)\)

\(\cos\left(\alpha\pm\beta\right)\;=\;\cos\left(\alpha\right)\cos\left(\beta\right)\;\mp\;\sin\left(\alpha\right)\sin\left(\beta\right)\)

\(\tan\left(\alpha\pm\beta\right)\;=\;\frac{\tan\left(\alpha\right)\;\pm\;\tan\left(\beta\right)}{1\;\mp\;\tan\left(\alpha\right)\tan\left(\beta\right)}\)

\(ctn\left(\alpha\pm\beta\right)\;=\;\frac{ctn(\alpha)ctn(\beta)\mp\;1}{ctn(\alpha)\;\pm\;ctn(\beta)}\)

Для чего применяются

Формулы сложения показывают, как функции суммы или разности двух углов выражаются через функции самих углов. Так можно решить тригонометрическое выражение, когда точные значения функций рассматриваемых углов отсутствуют в таблицах.

Например, тангенс угла 15 градусов можно представить, как разность углов 45 и 30 градусов или любых других углов, тангенсы которых известны. Также формулы сложения используют при доказательстве других формул, например, двойного угла.

Формулы понижения степени

Для чего применяются

С их помощью можно приводить тригонометрические уравнения к уравнениям более низких степеней, вплоть до первой степени. Важно помнить, что при понижении степени аргумент увеличивается.

Общий вид 

Для четных n:

\(\sin^n\left(\alpha\right)\;=\;\frac{C_n^\frac n2}{2^n}\;+\;\frac1{2^{n-1}}\;\times\;\sum_{k=0}^{{\textstyle\frac n2}-1}{(-1)}^{{\textstyle\frac n2}-k}\;\times\;C_n^k\;\times\;\cos\left((n-2\times k)\times\alpha\right)\)

\(\cos^n\left(\alpha\right)\;=\;\frac{C_n^\frac n2}{2^n}\;+\;\frac1{2^{n-1}}\;\times\;\sum_{k=0}^{{\textstyle\frac n2}-1}C_n^k\;\times\;\cos\left((n-2\times k)\times\alpha\right)\)

Для нечетных n:

\(\sin^n\left(\alpha\right)\;=\;\frac1{2^{n-1}}\;\times\;\overset{\textstyle\frac{n-1}2}{\underset{k=0}{\sum{(-1)}^{\frac{n-1}2-k}\;\times\;}}C_n^k\;\times\;\sin\left((n-2\times k)\times\alpha\right)\)

\(\cos^n\left(\alpha\right)\;=\;\frac1{2^{n-1}}\;\times\;\overset{\textstyle\frac{n-1}2}{\underset{k=0}{\sum\;}}C_n^k\;\times\;\cos\left((n-2\times k)\times\alpha\right)\)

\(C_p^q\;=\;\frac{p!}{q!(p-q)!}\)

Это означает число сочетаний из p элементов по q.

Сумма и разность функций

В каком виде можно представить действия

Использование этих формул позволяет перейти от суммы или разности функций углов \(\alpha\) и \(\beta\) к произведению функций углов \(\frac{\alpha\;+\;\beta}2\;\) и \(\;\frac{\alpha\;-\;\beta}2\).

Примеры формул

\(\sin\left(\alpha\right)\;+\;\sin\left(\beta\right)\;=\;2\;\times\;\sin\left(\frac{\alpha\;+\;\beta}2\right)\;\times\;\cos\left(\frac{\alpha\;-\;\beta}2\right)\)

\(\sin\left(\alpha\right)\;-\;\sin\left(\beta\right)\;=\;2\;\times\;\sin\left(\frac{\alpha\;-\;\beta}2\right)\;\times\;\cos\left(\frac{\alpha\;+\;\beta}2\right)\)

\(\cos\left(\alpha\right)\;+\;\cos\left(\beta\right)\;=\;2\;\times\;\cos\left(\frac{\alpha\;+\;\beta}2\right)\;\times\;\cos\left(\frac{\alpha\;-\;\beta}2\right)\)

\(\cos\left(\alpha\right)\;-\;\cos\left(\beta\right)\;=\;-2\;\times\;\sin\left(\frac{\alpha\;+\;\beta}2\right)\;\times\;\sin\left(\frac{\alpha\;-\;\beta}2\right)\)

Произведение тригонометрических функций

Для чего используются

В некоторых случаях применение формул произведения помогает упростить преобразование тригонометрического выражения.

Переход к сумме, примеры

Формулы умножения выводятся из формул суммы и разности. Рассмотрим, как от этих формул можно перейти к формулам произведения и наоборот.

Применив вычитание из косинуса суммы косинуса разности, мы получим:

\(\sin\left(\alpha\right)\sin\left(\beta\right)\;=\;\frac12(\cos\left(\alpha-\beta\right)\;-\;\cos\left(\alpha+\beta\right))\)

Сложим косинус суммы и косинус разности:

\(\cos\left(\alpha-\beta\right)\;=\;\cos\left(\alpha\right)\cos\left(\beta\right)\;+\;\sin\left(\alpha\right)\sin\left(\beta\right)\)

\(\cos\left(\alpha+\beta\right)\;=\;\cos\left(\alpha\right)\cos\left(\beta\right)\;-\;\sin\left(\alpha\right)\sin\left(\beta\right)\)

\(\cos\left(\alpha+\beta\right)\;+\;\cos\left(\alpha-\beta\right)\;=\;2\cos\left(\alpha\right)\cos\left(\beta\right)\)

Следовательно:

\(\cos\left(\alpha\right)\cos\left(\beta\right)\;=\;\frac12(\cos\left(\alpha-\beta\right)\;-\;\cos\left(\alpha+\beta\right))\)

Сложим синус суммы и синус разности:

\(\sin\left(\alpha+\beta\right)\;=\;\sin\left(\alpha\right)\cos\left(\beta\right)\;+\;\sin\left(\beta\right)\cos\left(\alpha\right)\)

\(\sin\left(\alpha-\beta\right)\;=\;\sin\left(\alpha\right)\cos\left(\beta\right)\;-\;\sin\left(\beta\right)\cos\left(\alpha\right)\)

\(\sin\left(\alpha\right)\cos\left(\beta\right)\;=\;\frac12(\cos\left(\alpha-\beta\right)\;-\;\cos\left(\alpha+\beta\right))\)

Формулы тройного угла

Эти тригонометрические формулы позволяют выразить функции двойных и тройных углов через функцию одинарного угла. Вывод этих формул базируется на формулах сложения.

\(\sin\left(3\alpha\right)\;=\;3\;\times\;\sin\left(\alpha\right)\;-\;4\;\times\;\sin^3\left(\alpha\right)\)

\(\cos\left(3\alpha\right)\;=\;4\;\times\;\cos^3\left(\alpha\right)\;-\;3\;\times\;\cos\left(\alpha\right)\)

\(\tan\left(3\alpha\right)\;=\;\frac{3\;\times\;\tan\left(\alpha\right)\;-\;\tan^3\left(\alpha\right)}{1\;-\;3\;\times\;\tan^2\left(\alpha\right)}\)