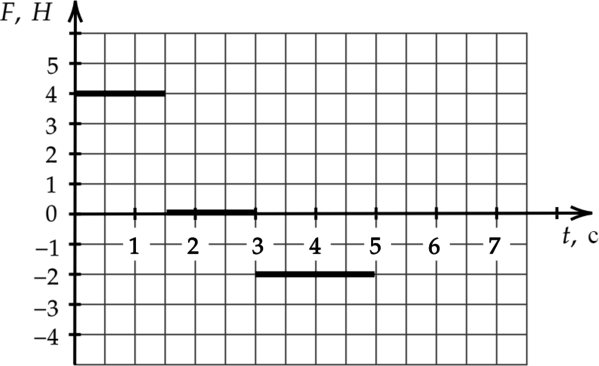Основной закон динамики материальной точки
Динамика материальной точки — основной закон
Динамика – это раздел механики, изучающий закономерности, которыми описано движение материальных тел под действием сил.
К основным законам динамики и теоретической механики относят законы Галилея и Ньютона. Смысл или задачи динамики:
- определить, какая сила действует на точку, находящуюся в движении по определенному закону;
- определить, какими закономерностями описано движение точки, на которую действуют силы.
Первый закон Ньютона гласит, что любая материальная точка находится в равновесии и покое, или равномерно прямолинейно движется до того момента, пока ее состояние не изменится от воздействия других тел.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Инерциальными системами называют такие системы отсчета, в которых выполним первый закон Ньютона.
Инертностью является стремление тела сохранять состояние покоя (быть неподвижным) или равномерного прямолинейного движения.
Согласно свойству инертности, первый закон Ньютона принято называть «законом инерции». Исходя из него, можно сделать вывод о существовании инерциальных систем отсчета, в которых этот закон выполняется. Для описания воздействия, о котором идет речь в первом законе Ньютона, введено понятие силы.
Сила – представляет собой векторную величину, меру механического воздействия на тело или материальную точку со стороны других тел, в результате которого скорость движения тела меняется, то есть приобретает определенное ускорение.
Второй закон Ньютона является основным законом динамики. Сформулирован он, таким образом: ускорение а, которое приобретает материальная точка или тело, пропорционально вызывающей его силе F и совпадает с ней по направлению \(a = F/m\) или \(F = ma = m(dv/dt).\)
В данном законе используется положительный скалярный коэффициент пропорциональности m, который является постоянным для любого определенного тела и называется массой. Второй закон Ньютона работает только в условиях инерциальных систем. Масса представляет собой меру инертности тела.
Таким образом, чем больше инертность тела и его масса, тем меньшее ускорение оно способно приобрести, когда не него воздействует одна и та же сила. Для того чтобы сравнить массы m1 и m2 пары тел, будет достаточно сопоставить их ускорения а1 и а2, которые тела приобретают под действием одинаковой силы:
\(m1/m2 = a2/a1\)
Как правило, для расчета массы тела ее сравнивают с массой эталонных тел или гирь, взвешивая их на рычажных весах. Данный способ основан на определении веса тела, который составляет:
\(P = mg\)
где g является величиной ускорения свободного падения, одинаковой для любых тел.
Исходя из этого, можно сделать вывод:
\(m2/m1 = P2/P1\)
Единицами измерения массы тела являются килограммы, а силы – ньютоны. Согласно определению, один ньютон равен силе, которая телу массой один килограмм сообщает ускорение в один метр на секунду в квадрате.
Уравнение движения материальной точки, то есть основной закон динамики:
\(F = d(mv)/dt = dp/dt\)
В данном случае векторная величина p= mv является импульсом, то есть количеством движения материальной точки.
Исходя из предложенной формулировки, второй закон Ньютона можно перефразировать, таким образом: скорость изменения импульса материальной точки равна действующей на нее силе.
В основном законе динамики материальной точки определен принцип причинности в классической механике: если известно исходное состояние материальной точки, включая ее координаты и начальную скорость, и действующая на эту точку сила, то по уравнению движения материальной точки можно определить ее состояние в любой будущий момент времени.
В механике справедлив принцип независимости действия сил, согласно которому в том случае, когда материальная точка подвергается воздействию одновременно нескольких сил, каждая из этих сил сообщает материальной точке ускорение, определенное вторым законом Ньютона, как будто другие силы отсутствуют. Таким образом, ускорение а, которое приобрела материальная точка с массой m под действием одновременно приложенных к ней сил F1,F2,...,Fn равно:
\(a=ai= Fi/m=(1/m) Fi=F/m\)
где F = Fi – является результирующей силой.
В случае, когда материальная точка испытывает воздействие одновременно нескольких сил, по второму закону Ньютона определяется результирующая сила F. Если траектория плоская, то вектор F направлен к центру кривизны траектории, как и вектор а. Данный вектор включает две составляющие:
- касательная к траектории (касательная или тангенциальная сила, Ft);
- нормальная к траектории (нормальная или центростремительная сила, Fn).
\(F =Ft +Fn\)
\(аt =Ft /m\)
\(an =Fn/m\)
\(F_{n}=\frac{mv^{2}}{R}\)
где R – является радиусом кривизны траектории.
При Fn= 0 движение будет прямолинейным. Если \(Fn= const\), то это движение по окружности (для пространственной траектории – по винтовой линии). При Ft= 0, движение будет равномерным. Если Ft = const, то можно наблюдать равноускоренное движение (если вектор Ft совпадает по направлению с вектором скорости v, то движение равноускоренное; если эти векторы направлены в разные стороны, то движение равнозамедленное).
Исходя из этого, можно переформулировать первый закон Ньютона: материальная точка в инерциальной системе отсчета обладает нулевым ускорением, когда равнодействующая сил равна нулю, либо другие тела не воздействуют на рассматриваемое тело.
Первый закон Ньютона может быть выведен из второго закона Ньютона. Но первая закономерность отличается самостоятельностью, так как является постулатом и подтверждает существование инерциальных систем отсчета.
По третьему закону Ньютона две материальные точки действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны вдоль прямой, соединяющей эти точки:
\(F12= -F21\)
где F12 – является силой, которая действует на первую материальную точку со стороны второй; F21 – представляет собой силу, действующую на вторую точку со стороны первой.
Способы описания движения материальной точки
Существует несколько методов, описывающих перемещение материальной точки. В том случае, когда имеется информация о траектории движения точки, целесообразно воспользоваться естественным способом. Траектория представляет собой комплекс точек в пространстве, которые пересекает материальная точка в процессе движения. Это линия, которую точка описывает в пространстве.
Координатный способ следует начинать с определения положения координат точки. В том случае, когда точка находится в движении, можно наблюдать изменения ее координат в течение времени. Исходя из зависимости координат точки от времени, можно сказать, что данные координаты представляют собой функции времени.
Форма траектории определяет характер движения: при траектории в виде прямой линии говорят о прямолинейном движении точки, а в виде кривой – о криволинейном движении.
Используя векторный способ, положение точки задают с помощью радиус-вектора. В процессе движения материальной точки радиус-вектор, который задает ее положение, меняется со временем, то есть представляет собой функцию времени r=r(t). В том случае, когда единичные векторы i, j, k направлены вдоль осей x, y и z, а также i = j = k = 1, закон движения можно записать так:
\(r(t) = x(t)i + y(t)j + z(t)k.\)
Импульс, кинематика и ускорение
Основные кинематические характеристики:
- скорость;
- ускорение.
Скорость \(\vec v\) является векторной величиной, характеризующей направление и быстроту движения.
Скорость для расчета средней скорости:
\(\vec v=\frac{\Delta\vec r}{\Delta t}\)
где \(\Delta\vec r\) — является перемещением, \(\Delta t\) — время, в течение которого точка переместилась.
Символ ∆ используют для обозначения разности однотипных величин или совсем маленьких интервалов.
Расчет мгновенной скорости можно выполнить в том случае, когда \Delta t\rightarrow0 и вектор перемещения совпадает с путем перемещения:
\(\vec v=\frac{d\vec r}{dt}=\frac{dS}{dt}\)
Ускорение тела (а) – представляет собой величину, определяемую через отношение изменения скорости перемещения тела к длительности временного интервала, в течение которого скорость менялась.
Формула ускорения:
\(a=\frac{\Delta V}{\Delta t}\)
Мгновенное ускорение имеет место в том случае, когда среднее ускорение за промежуток ∆t → 0, м/с²:
\(a=\frac{dv}{dt}\)
Импульс \(\vec p\) является векторной величиной, которая рассчитывается по формуле \(\vec p=m\times\vec v \)
С помощью импульса можно определить, каким образом, механическое движение передается от одного материального тела к другому.
Импульсом силы \(\vec Fdt\) называют векторную величину, совпадающую по направлению с направлением силы и численно равную произведению силы и времени ее воздействия на тело.
Динамика предусматривает несколько сил, которые могут оказывать воздействие на тело:
- сила притяжения;
- сила упругости;
- сила трения.
Согласно закону всемирного тяготения, открытым Ньютоном, сила F гравитационного притяжения между двумя телами массами \((m_1 \ и \ m_2)\), удаленными друг от друга на расстояние (r), прямо пропорциональна обеим массам, обратно пропорциональна расстоянию в квадрате, и действует вдоль прямой линии, на которой расположены тела.
Формула силы притяжения:
\(F=G\times\frac{m_1\times m_2}{r^2}\)
где G — является гравитационной постоянной, которая составляет \(6,67\times10^{-11} Н*м²/кг².\)
Силой упругости называют такую силу, которая возникает в процессе упругой деформации тела.
Формула силы упругости:
\(F=-k\times x\)
где x — является величиной деформации, k — коэффициент упругости, а знак «минус» говорит о том, что направление силы упругости всегда противоположно направлению смещения тела.
Силу трения можно наблюдать в том случае, когда объекты или их части в процессе движения соприкасаются. Виды силы трения:
- сухое — сила скольжения и сила покоя;
- вязкое, возникает в том случае, когда перемещаются слои жидкости или газа.
Формула силы сухого трения:\(F=k\times N \),
где N — является силой нормального давления, а k — коэффициент сухого трения.
Формула силы вязкого трения:
\(F=-α\times V\)
α — коэффициент вязкого трения.
Момент инерции, величина I для тел разной формы
Во время движения тела, при отсутствии стороннего воздействия, можно говорить о том, что проявляется инерция. Аналогичное явление наблюдают при вращении тела вокруг оси. В этом случае имеет место момент инерции.
Момент инерции является скалярной величиной, которая измеряет инертность тела при осевом вращении.
Чем больше масса тела, тем сложнее задать ему поступательное движение путем толкания. Масса тела определяет степень его инертности и представляет собой меру инертности. В случае вращательного движения мерой инертности является момент инерции.
В физике задачи на момент инерции решают с помощью теоремы Гюйгенса-Штейнера.
Момент инерции для тела, вращающегося вокруг определенной оси, равен сумме слагаемых единиц: момент инерции предмета, который вращается вокруг оси, параллельной данной, и проходящей через центр масс, а также произведения массы на расстояние между осями, возведенное в квадрат.
Формула для теоремы Гюйгенса-Штейнера:
\(I_{z}=I_{C}+md^{2}\)
d – является расстоянием между осями, m – определяет массу тел, Iz – момент инерции относительно рассматриваемой оси, а Ic – относительно оси, которая проходит через центр масс.
Момент инерции измеряют в килограммах, умноженных на метр в квадрате, кг·м².
Формулы определения момента инерции некоторых однородных тел, обладающих простой формой, исходя из характеристик осей вращения:
- момент инерции точечного предмета или полого цилиндра, обладающего тонкими стенками с массой m и радиусом r, равен \(mr^{2}\);
- момент инерции диска или сплошного цилиндра равен \(\frac{1}{2}mr^{2}\);
- момент инерции цилиндра, который обладает толстыми стенками, внешним радиусом r2 и внутренним – r1, равен \(m\frac{r_2^2+r_1^2}{2}\);
- момент инерции сплошного цилиндра, ось вращения которого перпендикулярна образующей цилиндра, расположенной по центру масс, равен\( \frac{1}{4}m\times r^{2}+\frac{1}{12}m\times l^{2};\)
- момент инерции цилиндра, обладающего тонкими стенками и осью, которая перпендикулярна к цилиндру и проходит через центр масс, равен \(\frac{1}{2}m\times r^{2}+\frac{1}{12}m\times l^{2}\);
- момент инерции стержня прямой тонкой формы, обладающего осью в виде перпендикуляра к стержню, которая проходит через центр масс, равен \(\frac{1}{12}m\times l^{2}\);
- момент инерции сферы с тонкими стенками и осью по центру равен \(\frac{2}{3}mr^{2}\);
- момент инерции шара с осью по центру равен\( \frac{2}{5}mr^{2}\);
- момент инерции равнобедренного треугольника с осью, которая перпендикулярна его плоскости и проходит через вершину, равен \(\frac{1}{24}m(a^{2}+12h^{2}).\)
Примеры решения задачи
Мяч обладает массой 1,5 кг и совершает движение по горизонтальной оси Ох. При этом на него действует сила F. Вначале мяч находился в покое. Представлен график зависимости силы F от времени t. Требуется определить импульс мяча в конце 4 секунды.
Решение
Согласно закону изменения импульса:
\(\sum F=\frac{\Delta p}{\Delta t}\)
В том случае, когда сила постоянна, импульс можно определить:
\(p=F_1(t_2-t_1)+F_2(t_3-t_2)+F_3(t_4-t_3)=4 \cdot(1,5-0)+0\cdot(3-1,5)+(-2)\cdot(4-3)=4\)
Ответ: 4 кг • м/с
Брусок массой 15 кг толкают с силой 12 Н по направлению движения. Требуется рассчитать ускорение бруска в инерциальной системе отсчета, которая связана со льдом.
Решение
По второму закону Ньютона:
\(\vec{F} = m\vec{a}\)
\(a=\frac{F}{m} = \frac {12}{15}= 0{,}8\)
Ответ: 0,8 м/с2
Рисунок демонстрирует силы, которые оказывают воздействие на материальную точку. Требуется определить модуль равнодействующей данных сил.
Решение
Согласно правилу параллелограмма, нужно сложить данные силы, то есть параллельно перенести каждую из сил в конец другой. Таким образом, равнодействующая будет равна 3 Н.
Ответ: 3 Н
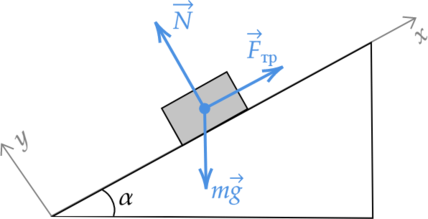
Брусок расположен на наклонной плоскости под углом \alpha=30^{\circ} и находится в состоянии покоя. Масса бруска 0,1 кг. Необходимо определить силу трения, действующую на брусок. Коэффициент трения между бруском и плоскостью равен \mu=0,7.
В первую очередь необходимо обозначить силы, которые воздействуют на брусок, а также ввести координатную плоскость. Ось Ох будет направлена вдоль наклонной плоскости, а Оу – перпендикулярно ей:
По второму закону Ньютона:
\(\vec{N}+m\vec{g}+\vec{F}_{\text{тр}}=m\vec{a}\)
где \(F_{\text{тр}}\) – сила трения, N – сила реакции опоры, a – его ускорение, m – масса тела
Исходя из того, что брусок находится в состоянии покоя, ускорение будет иметь нулевое значение. Второй закон Ньютона на ось Ох:
\(F_{\text{тр}} -mg \sin \alpha=0\)
\(F_{\text{тр}}=mg \sin \alpha\)
\(F_{\text{тр}}=0,1 \text{ кг} \cdot 10 \text{ Н/кг} \cdot \frac{1}{2}=0,5\text{ Н }\)
Ответ: 0,5 Н
Ящик на веревке поднимают вверх. Общий рисунок демонстрирует зависимость проекции скорости \bf\upsilon ящика на ось, направленную вертикально вверх, от времени t. Требуется рассчитать, какой массой обладает ящик, если известна сила натяжения веревки в 275 Н.
Решение
По результатам исследования в данном случае имеет место линейное изменение скорости ящика. Таким образом, ускорение тела равно:
\(a=\dfrac{\upsilon-\upsilon_{0}}{t}=\dfrac{4\text{ м/c$^2$}-1\text{ м/c$^2$}}{3\text{ c}}=1\text{ м/c$^2 $}\)
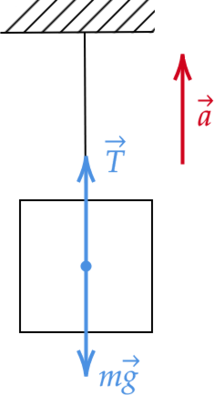
Следует изобразить силы, которые действуют на тело:
Далее можно спроецировать силы на ось Oy. По второму закону Ньютона:
\(T-mg=ma \ m(g+a)=T m=\frac{T}{(g+a)}\)
\(m=\dfrac{275\text{ H}}{10\text{ м/c$^2$}+1\text{ м/c$^2$}}=25\text{ кг }\)
Ответ: 25 кг
Масса автобуса относится к массе машины, как \(\displaystyle \frac{m_1}{m_{2}}=5,6\). Необходимо выполнить анализ и определить, как относятся скорости транспортных средств \(\displaystyle \frac{v_{1}}{v_{2}}\) при условии, что отношение импульса автобуса к импульсу автомобиля равно \(\displaystyle \frac{p_{1}}{p_{2}}= 2,8.\)
Решение
Исходя из формулы импульса получим параметр:
\(p=mv p_{1}=m_{1}v_{1}\)
\(p_{2}=m_{2}v_{2} \frac{p_{1}}{p_{2}}=\frac{m_{1}v_{1}}{m_{2}v_{2}} \frac{v_{1}}{v_{2}}= \frac{p_{1}m_{2}}{p_{2}m_{1}} =\frac{2,8}{5,6} =0,5\)
Ответ: 0,5
Задача 7
Отношение массы трамвая к массе автобуса \(\displaystyle \frac{m_1}{m_2}=4\). Трамвай движется со скоростью \(v_1= 5 м/с\). Отношение импульса трамвая к импульсу автобуса составляет 1. Требуется рассчитать скорость автобуса.
Решение
\(p=mv\)
\(\frac{p_1}{p_2}= \frac{m_1v_1}{m_2v_2} \Rightarrow v_2=\frac{m_1v_1p_2}{p_1m_2}=4\cdot 5\cdot {1} =20\)
Ответ: 20 м/с.
Требуется определить импульс инерции модели в виде однородного диска, масса и радиус которого известны. Ось вращения проходит через его центр.
Решение
В первую очередь следует разбить диск на тонкие кольца, радиусы которых соответствуют амплитуде от 0 до R. Взяв одно из них и обозначив его радиус буквой r, а массу – dm, можно подставить данные значения в формулу, согласно теореме Гюйгенса-Штейнера. С учетом значений формула момента инерции для массы кольца будет записана следующим образом:
\(I=\int_{0}^{R}{\rho 2\pi rdrr^{2}dz}=2\pi \rho dz\int_{0}^{R}{r^{3}dr}=\frac{\pi \rho dzR^{4}}{2}=\frac{mR^{2}}{2}\)
Ответ: \(\frac{mR^{2}}{2}\)
Условия аналогичны предыдущей задаче. Только в данном случае ось проходит через центр радиуса. Необходимо найти момент инерции.
Решение
Из предыдущего примера можно использовать величину момента инерции относительно оси, которая при колебании проходит через центр масс. Согласно формуле Штейнера, получим:
\(I=I_{c}+md^{2}\)
\(I=\frac{mR^{2}}{2}+m(\frac{R^{2}}{4})=\frac{3}{4}mR^{2}\)
Ответ: \(\frac{3}{4}mR^{2}\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так