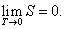В чем заключается суть третьего начала термодинамики

Формулировка третьего начала термодинамики

Нернст

Тепловая теорема немецкого химика Вальтера Нернста, также известная как третий закон термодинамики, была разработана в 1906 году. В Берлине Нернст и его ученики провели множество важных физико-химических измерений, в частности, определили удельные теплоемкости твердых тел при очень низких температурах и плотности паров при высоких температурах. Все это рассматривалось с точки зрения квантовой теории. За это исследование Вальтер Нернст получил Нобелевскую премию по химии в 1920 году.

Теорема гласит, что по мере приближения к абсолютному нулю изменение энтропии ΔS при химическом или физическом превращении приближается к 0. Ни один процесс, каким бы идеализированным он ни был, не может уменьшить энтропию системы до ее абсолютного нулевого значения за конечное число операций. Математически это можно выразить следующим образом:

Источник: edu.tltsu.ru

Приведенное выше уравнение — это современное изложение теоремы. Нернст часто использовал форму, в которой не использовалось понятие энтропии. По словам ученого, «невозможно, чтобы процесс привел энтропию данной системы к нулю за дискретное и конечное число шагов».

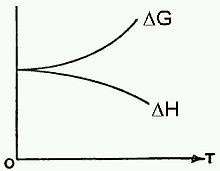
Другой способ взглянуть на теорему — начать с определения свободной энергии Гиббса (G), G = H - TS, где H означает энтальпию. Для перехода от реактивов к продуктам при постоянной температуре и давлении уравнение принимает вид ΔG = ΔH - TΔS.

Источник: wikiwand.com

В пределе T = 0 уравнение сводится к простому ΔG = ΔH, как показано на рисунке, что подтверждается экспериментальными данными. Однако из термодинамики известно, что наклон кривой ΔG равен -ΔS. Поскольку наклон, показанный здесь, достигает горизонтального предела 0 при T → 0, из этого следует, что ΔS → 0, что является тепловой теоремой Нернста.

Значение данной теоремы заключается в том, что она была позже использована Максом Планком для получения третьего закона термодинамики, согласно которому энтропия всех чистых, идеально кристаллических однородных материалов, находящихся в полном внутреннем равновесии, равна 0 при абсолютном нуле.

Планк

Немецкий физик Макс Планк позже использовал теорему Нернста для определения третьего закона термодинамики в терминах энтропии и абсолютного нуля.

Некоторые материалы (например, любое аморфное твердое тело) не имеют четко определенного порядка при абсолютном нуле. В таких материалах (например, в стекле) некоторая конечная энтропия сохраняется и при абсолютном нуле, поскольку микроскопическая структура системы (атом за атомом) может быть устроена по-разному (W ≠ 1). Эта постоянная энтропия известна как остаточная энтропия, которая представляет собой разницу между неравновесным и кристаллическим состоянием вещества, близким к абсолютному нулю.

Это уравнение, связывающее микроскопические детали, или микросостояния, системы (через W) с ее макроскопическим состоянием (через энтропию S), является ключевой идеей статистической механики.

Суть третьего начала термодинамики

Третий закон термодинамики касается поведения систем при приближении температуры к абсолютному нулю. Он связывает тепло и энтропию при этой предельно низкой температуре для кристаллов, которые относятся к любому твердому материалу, состоящему из атомов, расположенных в определенном, симметричном порядке. Третий закон термодинамики гласит: «Энтропия идеального кристалла равна нулю, когда температура кристалла равна абсолютному нулю (0 К)». Во-первых, идеальный кристалл означает, что в нем нет примесей, достигнуто термодинамическое равновесие и он находится в кристаллическом состоянии, когда все атомы/ионы/молекулы занимают четко определенные позиции в высокоупорядоченной кристаллической решетке. Это исключает аморфные твердые вещества, такие как стекло, которые не имеют упорядоченной кристаллической структуры и не достигли термодинамического равновесия.

В нечистых кристаллах или кристаллах с нарушенным выравниванием некоторое количество энергии будет связано с несовершенствами, поэтому энтропия не может стать нулевой. Теоретически можно вырастить идеальный кристалл, в котором все места в решетке заняты одинаковыми атомами. Однако принято считать, что достичь температуры абсолютного нуля невозможно. Поэтому вся материя содержит, по крайней мере, некоторое количество энтропии, обусловленное наличием тепловой энергии.

Третий закон не является интуитивным, он был выведен эмпирическим путем, поскольку энтропия системы всегда приближается к одному и тому же минимальному значению по мере понижения абсолютной температуры и приближения ее к нулю.

Математическое представление Третьего закона термодинамики обычно выглядит следующим образом: уравнение изменения энтропии:

ΔS = ∫T2T1 (ΔQ/T)

В этом уравнении:

ΔS — изменение энтропии,
ΔQ — бесконечно малое количество добавленного или удаленного тепла,
T — абсолютная температура.

Отношение к тепловым двигателям

Согласно принципу Карно, который устанавливает пределы максимальной эффективности, которую может иметь любой тепловой двигатель, - это КПД Карно. Этот принцип также гласит, что эффективность цикла Карно зависит исключительно от разницы температур горячего и холодного резервуаров.

η_max = η_carnot = 1 - (T_C/T_H),

где:

КПД цикла Карно, т.е. отношение = W/QH работы, совершаемой двигателем, к тепловой энергии, поступающей в систему из горячего резервуара.
TC — абсолютная температура (Кельвины) холодного резервуара,
TH — абсолютная температура (Кельвины) горячего резервуара,
Согласно третьему закону, TC никогда не может быть равна нулю. Поэтому тепловой двигатель со 100% эффективностью невозможен.

Примеры решения задач

Решение:

Рассчитайте изменение энтропии, используя стандартные энтропии, как показано выше:
ΔS°=(1mol)(70.0Jmol−1K−1)−(1mol)(188.8Jmol−1K−1)=−118.8J/K.

Значение ΔS° отрицательно, как и ожидалось для данного фазового перехода (конденсации).

Решение:

Запомните: ΔS = ∫T2T1 (ΔQ/T). Здесь, поскольку вода кипит, начальная и конечная температуры одинаковы, т.е. T1=T2=100°C. Переведем это в Кельвины (единицы СИ), чтобы получить 100 + 273,15 = 373,15k.
ΔQ — это тепло, выделяемое при превращении жидкой воды в пар, скрытая теплота парообразования. Таким образом, ΔQ = 2,26x10⁶моль^-1.
Подставим эти данные в ΔS = ΔQ/T, чтобы получить: ΔS = 2,26x10⁶моль^-1 / 373,15k.
Использование этого уравнения и подхода позволяет рассчитать изменение энтропии и предсказать спонтанные реакции, эффективность использования энергии или даже данные для создания технологий охлаждения.

Решение:

Изменение энтропии, связанное с изменением температуры: ΔS = ∫(Cp/T)dT, где Cp — молярная теплоемкость газа при постоянном давлении.

Для идеального газа, молярная теплоемкость при постоянном давлении Cp выразим так:
Cp = (5/2)R, где R — универсальная газовая постоянная.

При постоянной температуре T, работа, совершенная при изменении объема газа, определяется формулой:
W = -P(ΔV), где P — давление газа, ΔV — изменение объема газа.

Применим уравнение состояния идеального газа: PV = nRT, где n — количество вещества газа, R — универсальная газовая постоянная, получим:
P1V1 = nRT,
P2V2 = nRT.

Подставим эти значения в формулу для работы идеального газа:
W = -P1(ΔV), где ΔV = V2 - V1.

Ответ: Таким образом, работа, совершенная газом, равна:
W = -P1(V2 - V1).