Формулы по физике за 9 класс
Формулы по физике за 9 класс: основные разделы
Программа обучения по предмету физика в 9 классе включает в себя несколько разделов: кинематика и динамика, которые в свою очередь состоят из подразделов. Таким образом ученики старшей школы изучают механические колебания и волны, законы взаимодействия и движения тел, электромагнитные явления, строение атомов и их ядер, основные законы механики. В школьную программу девятого года обучения также входят основные свойства света: интерференция, преломление и дисперсия.
Кинематика
Кинематика — один из разделов механики. Кинематика изучает механическое движение тел и способы его описания, независимо от причин этого движения. В данном случае под механическим движением подразумевается любое изменение положения какого-либо тела полностью или частично относительно других тел, случившееся с течением времени.
В Кинематике изучают простые виды движения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Равномерное прямолинейное движение
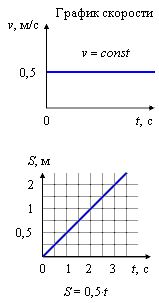
Понятие равномерного прямолинейного движения заключается в том, что тело движется по прямой с одинаковой скоростью, то есть за равные промежутки времени тело перемещается на одинаковое расстояние. В таком случае скорость тела остается постоянной, однако является векторной величиной.
Скорость может быть как положительной, так и отрицательной. Все зависит от того, в каком направлении оси X (положительном или отрицательно) направлен вектор скорости. Если тело находится в покое, то его скорость равняется нулю, а координата не меняется в течение времени.
При равномерном прямолинейном движении координата тела вычисляется по следующей формуле:
x = x0 + v · t
В этой формуле x0 – начальная координата, x – конечная координата, v – скорость, t – время.
Если начальная координата — это начало движения и x0 = 0, то формулу можно сократить до x1 = v · t.
Если x0 = 0, то пройденный путь S будет равен координате x. Из этого утверждения можно получить формулу прямолинейного равномерного движения относительно пройденного телом расстояния:
S = v · t.
Из этого можно вывести формулы относительно скорости и времени:
v= S/t и t = S/v.
Скорость и время также можно выразить из полной формулы для тех случаев, когда x0 не равно 0:
v = (x1 — x0)/t и t = (x1 — x0)/v.
Равноускоренное прямолинейное движение
В случае равноускоренного прямолинейного движения тело изменяет скорость своего движения на одинаковую величину за любые равные промежутки времени. Под ускорением в контексте данного определения понимается изменение значения скорости за единицу времени.
Скорость тела вычисляется по формуле:
v = v0 + a · t
В данной формуле v – конечная скорость, v0 – начальная скорость, a – ускорение, t – время.
В равноускоренном прямолинейном движении постоянной величиной является ускорение, а не скорость. Ускорение может быть больше или меньше нуля. В случае увеличения скорость, значение ускорения будет больше нуля, а в случае уменьшения — меньше.
Рассмотрим случай, если начальная скорость тела равно 0. Тогда его скорость через какое-либо время t будет равна произведению ускорения и этого времени:
v = at
Допустим, что нам известны текущая скорость тела и время, за которое тело развило указанную скорость из состояния покоя. Тогда мы можем определить ускорение:
a = v/t
В том случае, если начальная скорость тела не равна нулю, мы можем рассчитать конечную скорость тела по следующей формуле:
v = v0 + at
Взглянем на случаи, когда вектор скорости направлен в противоположном направлении (например, подброшенный камень, его скорость направлена в противоположную сторону от ускорения свободного падения) или в случае торможения. Тогда формула будет выглядеть следующим образом:
v = v0 – at
В случае свободного ускорения остальные формулы будут записываться так:
at = v – v0, a = (v – v)/t
А говоря о торможении, мы используем эти формулы:
at = v0 – v, a = (v0 – v)/t
Если тело останавливается, то нам следует использовать эту формулу:
a = v0/t
А если необходимо узнать, через какой отрезок времени тело остановится, то мы запишем формулу так:
t = v0/a
Обратимся к формуле, которая поможет найти путь, которое тело проходит при прямолинейном ускорении. Если при равномерном движении, оси времени и расстояния параллельны, то в случае равноускоренного движения ось движения либо возрастает, либо убывает. Тогда вместо прямоугольника, чью площадь мы вычисляли при равномерном движении, необходимо вычислить площадь трапеции.
Площадь трапеции равна полусумме оснований на высоту, таким образом мы получаем:
s = ½ · (v0 + v) · t
Пройденный путь определяется по формуле:
s = v0t + at2/2
Путь торможения рассчитывается с помощью этой формулы:
s = v02/(2a)
Равномерное движение по окружности
Говоря о равномерном движении по окружности, нужно понимать, что в этом случае вектор скорости тела изменяется (скорость направлена по касательным к окружности), а модуль скорости тела (числовое значение) остается постоянным.
Предположим, что необходимо вычислить модуль скорости за один оборот тела по окружности. Обозначим оборот как S, а время, за которое тело его совершило, как t. Тогда формула будет записываться следующим образом: v = s/t.
Однако, если мы говорим об одном обороте, то это называется период. То есть время, за которое тело совершает один оборот вокруг окружности. Он обозначается как T. И тогда формула одного оборота будет выглядеть так: v = s/T
Если S в данном случае это длина окружности (l), то формула принимает вид v = 2πR/T, в соответствии с формулой окружности l = 2\piR
Если необходимо найти период при известном модуле скорости, то формула примет вид T = 2\piR/v
Аналогично радиус можно найти через формулу R = ½ vT/\pi
Динамика
Динамика — раздел механики, изучающий предпосылки изменения в характере движения. Например, возникновение движения. Именно этот раздел изучает три закона Ньютона. В задачах динамики содержится решение таких вопросов как определение действующих на тело сил по характеру его движения и наоборот.
Законы Ньютона
Первый закон Ньютона гласит, что существуют такие системы отсчета, относительно которых тело движется прямолинейно и равномерно, или покоится, если на него не действуют другие тела или их действия скомпенсированы.
Введем основные величины:
Инерциальными называются системы отсчета, которые движутся равномерно прямолинейно относительно Земли. Все системы отсчета, которые движутся прямолинейно и равномерно относительно инерциальной, также являются таковыми. Если система отсчета движется с ускорением, то она — неинерциальная.
Сила — это физическая величина, которая характеризует действие одного тела на второе. В результате этого действия второе тело получает ускорение в инерциальной системе отсчета. Измеряется в ньютонах.
Масса — это физическая величина, которая количественно характеризует инертность тела. Измеряется в килограммах.
Взглянем на тело, на которое действует сила с модулем равным 1 Н. Так как изначально тело массой 1 кг находилось в покое в инерциальной системе, модуль его ускорения будет равен 1 м/с2.
В соответствии со вторым законом Ньютона сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение. Это основной закон динамики.
Для выведения второго закона Ньютона и формулы, где F = ma, необходимо обобщить два факта:
- если на два тела, масса которых различна, подействовать равной силой, то ускорения, которые приобретут тела, будут обратно пропорциональны массам;
- если на одно и то же тело действуют силы разной величины, то ускорения тела будут прямо пропорциональны приложенным силам.
Благодаря этому закону, возможно вычислить не только силу, действующую на тело, но и ускорение. Для этого нужно использовать формулу \[w = \frac{F}{m}\]
В векторной форме второй закон Ньютона записывается как ma = mg + N + Fтр
Третий закон Ньютона гласит, что силы, с которыми две материальные точки воздействуют друг на друга, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки.
Выразить закон формулой можно следующим образом F1 = -F2
В случае взаимодействия тел силы имеют одинаковую природу, однако, они приложены к разным телам. Таким образом эти силы не могут уравновешивать друг друга, а складывать можно только силы, приложенные к одному телу.
Силы в природе
В соответствии с законом Гука, при деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Природа этой силы состоит в электромагнитном взаимодействии между атомами и молекулами вещества. Эта сила называется упругость.
Говоря о малых деформациях (если |x| < l) сила упругости пропорциональна деформации тела и направлена в противоположную сторону от перемещения частиц тела при деформации. Исходя из этого формула выглядит следующим образом Fx = Fупр = -kx
В данном случае коэффициент k — жесткость тела, она измеряется в ньютонах на метр (Н/м).
Физике свойственен другой способ записи закона Гука. В его записи используются понятия относительной деформации и напряжения. Относительная деформация ε = x / l, а напряжение - это отношение силы к площади поперечного сечения деформированного тела δ = F / S = -Fупр / S.
Исходя из этого, закон Гука можно сформулировать так \[ε = \frac{E}{δ}\]
Коэффициент Е — это модуль Юнга. Он зависит исключительно от свойств материала. Размеры и форма не имеют значения.
Если говорить о случаях сложных деформациях, например в случае деформации изгиба, в формуле появляется сила N — сила реакции опоры. Эта сила направлена перпендикулярно поверхности соприкосновения. N = -mg
Сила всемирного тяготения
Закон всемирного тяготения говорит, что все тела притягиваются друг к другу с силами, прямо пропорциональными их массам и обратно пропорциональна квадрату расстояния между ними.
Эту силу можно вычислить по формуле F = G\fracMR32m = mg
g в данном случае — ускорение свободного падения, о котором говорилось выше. В данном случае g = G\fracMR32. Среднее значение ускорения свободного падения равно 9,81 м/с2.
R3 — это радиус Земли. Он равен 6,38·106 м.
G в формуле обозначает гравитационную постоянную. Она равна 6,67·10–11 Н·м2/кг2.
Движение тела под действием силы тяжести
Ускорение свободного падение является частным случаем равноускоренного прямолинейного движения. В этом случае ускорение всегда будет равно 9,8 м/с2 и обозначается буквой g. Таким образом g — это ускорение свободного падения.
Ускорение свободного падения можно вычислить по следующей формуле: g = GM3/(R3+H)2
В данном случае H — это гравитационная постоянная, M — масса земли, R — радиус земли, а H — высота падения тела.
Скорость тела под действием силы тяжести можно вычислить по формуле: v = gt
Высоту, с которой падает тело, можно вычислить по формуле H=gt2/2
Силы трения
Силой трения называют силу, характеризующую взаимодействие, возникающее в месте соприкосновения тел и препятствующее их относительному движению. Сила трения имеет электромагнитную природу.
Трение можно разделить на три вида: трение покоя, трение скольжения и трение качения.
Трение покоя — это трение, которое возникает при отсутствии перемещения соприкасающихся тел относительно друг друга.
Можно сказать, что эта сила не позволяет одному телу двигаться относительно другого. Эта сила направлена противоположно силе, приложенной извне параллельно поверхности соприкосновения. Сила трения покоя возрастает вместе с силой, которая стремится сдвинуть тело с места.
Трение скольжения возникает при действии на тело силе, превышающей максимальную силу трения покоя.
Это тело сдвигается с места и начинает дальнейшее движение. Сила трения скольжения всегда направлена в противоположную сторону от относительной скорости соприкасающихся тел.
Трение качения возникает в случае, если тело не скользит по другому телу, а катится наподобие колеса или цилиндра. Трение качения — это трение, которое возникает на месте их соприкосновения.
В виде формулы сила трения выглядит следующим образом: Fтр = μmg
В данном случае μ – коэффициент трения, m – масса тела, а g — ускорение свободного падения (постоянная величина 9,81 м/с2).
Движение тела под действием нескольких сил
Если на тело действуют несколько сил одновременно, то необходимо найти равнодействующую всех сил по формуле F = F1 + F2 + F3
Равнодействующая сила может быть равна нулю. В таком случае тело находится в состоянии покоя.
Закон сохранения в механике
Закон сохранения импульса гласит, что геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.
В виде формулы закон сохранения импульса выглядит следующим образом: p1 + p2 = p1’ + p2’ m1v + m2u = m1v’ + m2u’
В свою очередь импульсом тела называют величину, которая равна произведению массы тела на его скорость: p = mv.
Изменение импульса тела равно импульсу силы, который в свою очередь вычисляется по формуле P = Ft
Кинетическая энергия равна половине произведения массы тела и квадрата его скорости: Ek = mv2/2
Кинетическая энергия — это физическая величина, которая характеризует движущиеся тела. Выражается в Дж.
Закон сохранения энергии состоит в том, что полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остается неизменной при любых движениях тел системы.
Мощность — это величина, которая равна отношению совершенной работы к промежутку времени, за который она совершена. Выражается в Вт.
Вычисляется по формуле N = A/t
Коэффициент полезного действия (КПД) — это название величины, равной отношению полезной работы ко всей совершенной работе. Выражается в Дж.
КПД демонстрирует эффективность использования затраченной энергии. Коэффициент не может быть больше единицы, однако его можно выразить в процентах.
Вычисляется КПД по формуле η = Aп/Aз
Для выражения в процентах применяется формула η = Aп/Aз ∙ 100%
Движение жидкостей и газов по трубам
Закон Бернулли гласит, что давление жидкости, текущей в трубе, больше в тех частях трубы, где скорость ее движения меньше, и наоборот, в тех частях трубы, где скорость больше, давление меньше.
Уравнение Бернулли для горизонтальной трубы выглядит следующим образом \(\[p_{1} + \frac{\rhov_1^2}{2} = p_{2} +\frac{\rhov_2^2}{2}\]\)
В этом уравнении p1 и p2 — статические давления, а \rho — плотность жидкости. В данном случае статическое давление равно отношению силы давления одной части жидкости на другую к площади соприкосновения, когда скорость их относительного движения равна нулю.
Если труба не горизонтальная, то уравнение Бернулли примет следующую форму:
\(\[p_{1} + \rho gh_{1} + \frac{\rho \upsilonc_1^2}{2} = p_{2} + \rho gh_{2} + \frac{\rho \upsilonc_2^2}{2}\]\)
Примеры задач
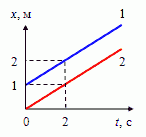
На рисунке представлены графики зависимости координаты двух тел от времени. Графики каких зависимостей показаны? Какой вид имеют графики зависимости скорости и пути пройденного телом, от времени?
Решение
На рисунке показаны графики равномерного движения тел.
- В начальный момент времени t = 0 первое тело имеет начальную координату хо1 = 1 м, второе тело — координату хо2 = 0.
- Оба тела движутся в направлении оси Х, так как координата возрастает с течением времени.
- Уравнение движения для равномерного прямолинейного движения имеет вид: x=xо+vхt.
Тогда для первого, второго тела соответственно:
x1=xо1+v1хt и x2=xо2+v2хt
или x1=1+v1хt и x2=v2хt.
Определим скорости первого и второго тела:
\(\[v_{1x} = \frac{x_{1} — 1}{t} = \frac{2 — 1}{2} = 0,5 м\с\]\)
\(\[v_{2x} = \frac{x_{2}}{t} = \frac{1}{2} = 0,5 м\с\]\)
Шар подвешен на невесомой нерастяжимой нити длиной l = 0,5 м. Какую минимальную горизонтально направленную скорость vo надо сообщить шару, чтобы он сделал полный оборот в вертикальной плоскости?
Решение:
Воспользуемся законом сохранения механической энергии при переходе шарика из нижнего положения в верхнее:
\(\[\frac{mv_0^2}{2} = mg2l + \frac{mv^2}{2} \]\)
В верхней точке на шарик будут действовать 2 силы: сила тяжести mg (направлена вниз) и сила натяжения нити T (также направлена вниз). Эти силы сообщают шарику центростремительное ускорение, направленное вниз — к точке подвеса, где l — длина подвеса или нерастяжимой нити.
maμ = mg + T
Поскольку шарик достиг верхней точки (T = 0, условие задачи), то \(\[ \frac{mv^2}{l} = mg \]\), отсюда v2 = gl
Сделаем подстановку и получим \(\[ \frac{mv_0^2}{2} = 2mgl + \frac{mgl}{2}\]\)
vo2 = g4l + gl = 5gl
vo = √(5gl)
Выполнив вычисления, получим: vo = √(5×10×0,5) = 5 (м/с).
Ответ: если шарик подвешен на нерастяжимой нити, его скорость должна составлять не менее 5 м/с.
Экваториальный радиус Земли равен 6370 км. Определить линейную и угловую скорости движения точек экватора при вращении Земли вокруг оси.
Решение:
Линейная скорость вращения ν точек земного экватора:
\(\[v = \frac{2\piR}{T}\]\)
При этом угловая скорость вращения w всех точек Земли равна:
\(\[w = \frac{2\pi}{T}\]\)
После вычислений у нас получится: ν = 463 м/с, w = 7,3×10−5 рад/с.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так