В чем суть закона сохранения момента импульса

Момент импульса и закон его сохранения

Закон сохранения импульса был сформулирован Рене Декартом в семнадцатом веке, но только в применении к поступательно движущимся телам, все точки которых смещаются в пространстве по одинаковым траекториям. Спустя сто лет другие ученые пришли к выводу, что для вращательного движения тоже существует свой закон сохранения.

Что это такое, краткое определение

Импульс — величина, характеризующая количество поступательного движения. Момент силы выполняет ту же роль по отношению к моменту импульса, что и просто сила по отношению к импульсу.

Скорости материальных точек, составляющих любое твердое тело, равны только при поступательном движении. Когда тело вращается, модуль скорости точки прямо пропорционален расстоянию от оси вращения r. Угловая скорость одинакова для всех точек, из которых состоит твёрдое тело, поэтому момент импульса предпочтительнее выразить через нее:

\(L\;=\;rmv\;=\;r\;m(\omega r)\;=\;mr^2\omega\;=\;I\omega\)

где \(I\) здесь — обозначение момента инерции, \(\omega\) — угловой скорости.

В квантовой механике для большинства частиц момент импульса вычислен экспериментально и имеет постоянное значение, точнее, постоянное соотношение с переменной Планка. Принцип неопределенности Гейзенберга накладывает ограничение на возможность вычислить все шесть переменных, от которых зависит момент импульса частицы. Одновременно можно узнать лишь величину его вектора и одну из его проекций.

Модуль собственного момента импульса частицы определяется спиновым квантовым числом s и рассчитывается по формуле:

\(L_{s} = \hbar\sqrt{s \times (s + 1)}\)

Формулировка, формула с доказательством

В классической механике момент импульса является третьей динамической переменной, для которой существует фундаментальный закон сохранения: при любых процессах в замкнутой системе её полный момент импульса остаётся неизменным.

Для равновесной механической системы закон выглядит так:

\(\sum_{i\;=\;0}^n\overrightarrow{L_i}\;=\;const\)

Для доказательства неизменности момента импульса можно рассмотреть его изменение за малый промежуток времени, найдя производную, и увидеть, когда это изменение равно нулю, что означает сохранение определенного значения момента импульса. Используя правило нахождения производной от произведения, получаем следующее выражение:

\(\frac{d\overrightarrow L}{dt}\;=\;\frac d{dt}\;(\overrightarrow r\times m\overrightarrow v)\;=\;\frac{d\overrightarrow r}{dt}\;\times\;m\overrightarrow v\;+\;\overrightarrow r\;\times\;\frac d{dt}(m\overrightarrow v)\;=\;\overrightarrow v\;\times\;m\overrightarrow v\;+\;\overrightarrow r\;\times\;\frac d{dt}(m\overrightarrow v)\)

Первое слагаемое в правой части результата равно нулю, потому что представляет собой векторное произведение параллельных векторов. Второе слагаемое — это векторное произведение того же радиус-вектора, который брали при расчёте момента инерции, на изменение импульса за малый промежуток времени, т. е. на силу:

\(\frac d{dt}(m\overrightarrow v)\;=\;\overrightarrow F\)

Момент силы имеет нулевое значение. Соответственно, производная момента импульса тоже будет иметь нулевое значение, и он останется неизменным. 

Примером может служить перемещение планет в гравитационном поле Солнца. Вектор момента импульса планеты относительно Солнца не меняется, так как линия действия силы гравитации проходит через него, и ее момент относительно этой точки равняется нулю.

Условия его выполнения в замкнутой системе

Закон сохранения момента импульса — проявление изотропности пространства, одинаковости его свойств по всем направлениям. Поворот замкнутой системы целиком не изменяет ее физических свойств, и момент ее импульса может изменяться лишь при наличии ненулевого момента внешних сил. Если тела внутри системы находятся в тех же условиях, что и в прежнем положении, поворот не отразится на ходе всех последующих явлений.

Так как момент импульса в классической механике существует не сам по себе, а относительно некой точки или оси, важно уточнить, что нужно измерять суммарный момент внешних сил относительно этой конкретной точки или оси. Но когда центр масс тела покоится, при переходе к другой точке отсчета внутри той же системы суммарный момент импульса не меняется.

Применение закона, примеры для твердого тела

Из закона сохранения момента импульса следует, что при отсутствии внешних влияний в процессе вращения системы вокруг оси любое изменение расстояния от тел до оси вращения должно сопровождаться изменением скорости их обращения вокруг этой оси. С увеличением расстояния скорость вращения уменьшается, так как увеличивается момент инерции, увеличивается угловая скорость и, как следствие, удлиняется обратно пропорциональный ей период вращения.

Балерина или фигуристка, кружась в пируэте, разводит руки, если хочет замедлить вращение, и прижимает их к телу, когда старается вращаться как можно быстрее.
В общем случае вектор момента импульса определяется векторным произведением

\(\overrightarrow L\;=\;\overrightarrow r\;\times\;m\overrightarrow v\)

Результатом является вектор, перпендикулярный плоскости, где лежат векторы сомножителей. Его направление можно определить по правилу правого винта, которое также называют правилом буравчика. Вращение правого винта от первого сомножителя ко второму по кратчайшей дуге приводит к его ввинчиванию в ту же сторону, в которую направлен результат векторного произведения. Модуль получившегося вектора равен произведению модулей векторов сомножителей на синус угла между ними:

\(\left|\overrightarrow L\right|\;=\;\left|\overrightarrow r\right|\;\times\left|\;m\overrightarrow v\right|\;\times\;\sin\left(\overrightarrow r,\;\;m\overrightarrow v\right)\)

Когда мы ищем момент импульса твердого тела, вектор угловой скорости и ось, вокруг которой вращается тело, должны совпадать по направлению. Это значит, что тело должно вращаться вокруг неподвижной оси, например, закрепленной подшипниками, или вокруг оси свободного вращения тела. Только тогда можно искать момент импульса через произведение момента инерции и угловой скорости.

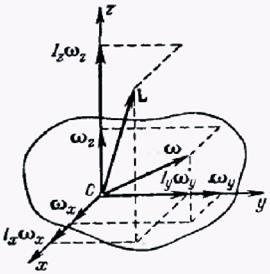
Когда вектор угловой скорости не совпадает с осями инерции, все его составляющие по трем осям будут отличаться от нуля.

В случае, если оси инерции совпадают с координатными, момент импульса вычисляют по формуле:

\(L\;=\;I_x\omega_{x\;}+\;I_y\omega_{y\;}+\;I_z\omega_{z\;}\)

В случае, если координатные оси и оси инерции не совпадают, приходится оперировать уже девятью величинами, которые образуют так называемый тензор инерции.

Задача

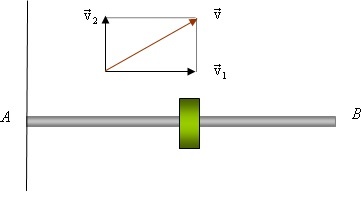
Гладкий однородный стержень массы М и длины l свободно вращается в горизонтальной плоскости вокруг неподвижной вертикальной оси, проходящей через его конец А. Из точки А в точку В скользит муфта массы m, найдите скорость муфты в момент, когда она достигнет точки В. Угловая скорость вращения равна \(\omega_0\) , момент инерции стержня относительно вертикальной оси равен \(\frac{Ml^2}3\).

Решение

Моменты сил, воздействующих на данную систему относительно вертикальной оси вращения, уравновешивают друг друга. Законы сохранения можно записать следующим образом:

\(\left\{\begin{array}{l}I\omega_0\;=\;(I\;+\;ml^2)\omega\\\frac{I\omega_0^2}2\;=\;\frac{I\omega^2}2\;+\;\frac{mv^2}2\end{array}\right.\)

На схеме \(v\) — скорость движения муфты в точке В в системе отсчета, связанной с Землей, \(v_1\) — скорость муфты в той же точке относительно стержня, \(v_2\) — линейная скорость самой точки В относительно Земли. Согласно закону сложения скоростей, v будет равняться сумме \(v_1\) и \(v_2\).

 

\(v_2 = \omega\;\times\;l\)

Так как \(v_1\) и \(v_2\) перпендикулярны:

\(v^2\;=\;v_1^2\;+\;\omega^2\;\times\;l^2\)

Следовательно:

\(v_1\;=\;\left[\frac{I\omega_0^2}m(I\;-\;\frac I{I\;+\;ml^2})\right]^\frac12\)

Подставим выражение момента инерции, данное в условиях задачи, и получим ответ:

\(v_1\;=\omega_0\;\times\;l\;\times\;{(\frac M{M\;+\;3m})}^\frac12\)