Арифметический корень натуральной степени

Что такое арифметический корень натуральной степени 

Поиск корня n-й степени в арифметике называют извлечением корня n-й степени.

Данная операция представляет собой обратное действие возведению в \( n-ю \) степень. В качестве доказательства можно привести следующие примеры:

\(\sqrt[3]{27} = 3\), так как \(3^3 = 27\)

\(\sqrt[4]{625} = 5\), так как \( 5^4 = 625\)

Основные свойства 

Объяснение данного понятия можно рассмотреть с помощью примеров:

\(\sqrt[3]{-27} = -3,\) так как \((-3)^3 = -27\)

\(\sqrt[5]{-32} = -2\), так как \( (-2)^5 = -32\)

В зависимости от числа а определяется количество решений. В качестве самостоятельного примера можно рассмотреть следующие уравнения:

  \(x^2 = 16 \iff x^2-16 = 0 \iff (x+4)(x-4) = 0 \iff x_1 = -4 \\ x_2 = 4\)

\(x^2 = -9 \lt 0 \iff x \in \varnothing\), решения отсутствуют

\(x^4 = 81 \iff x^4-81 = 0 \iff (x^2+9)(x^2-9) = 0 \iff (x^2+9)(x+3)(x-3) = 0 \iff x_1 = -3 \\ x_2 = 3\)

\(x^3 = 27 \iff x^3-27 = 0 \iff (x-3)(x^2+3x+9) = 0 \iff x = 3\)

\(x^3 = -27 \iff x^3+27 = 0 \iff (x+3)(x^2-3x+9) = 0 \iff x = -3\)

Исходя из рассмотренных примеров, можно сделать следующие выводы:

1. В том случае, когда \( n\) является четным числом, и \(a \ge 0\), уравнение имеет два решения: \(x = \pm \sqrt[n]{a}\).
2. Когда \(n\) представляет собой четное число, и \(x = \pm \sqrt[n]{a}\), уравнение решений не имеет.
3. Если \(n \)является нечетным числом, то уравнение  \(x^n = a \) обладает единственным решением  \(x = \pm \sqrt[n]{a}\) при любом  \(x^n = a.\)

Свойства, которые характерны для арифметических корней натуральной степени:

• \(\sqrt[n]{ab} = \sqrt[n]{a} \cdot \sqrt[n]{b}, \quad a \ge 0, b \ge 0, n \in \Bbb N\);
• \(\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}, \quad a \ge 0, b \gt 0, n \in \Bbb N\);
• \(\sqrt[n]{a^m} = (\sqrt[n]{a})^m, \quad a \ge 0, n \in \Bbb N, m \in \Bbb N\);
• \(\sqrt[n]{a^m} = \sqrt[np]{a^{mp}}, \quad a \ge 0, n \in \Bbb N, m \in \Bbb N, p \in \Bbb N\);
• \(\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}, \quad a \ge 0, n \in \Bbb N, m \in \Bbb N\);
• \(\sqrt[n]{a^n} = (\sqrt[n]{a})^n = a, \quad a \ge 0, n \in \Bbb N\).

Как решать задачи, формулы

В качестве примера можно привести несколько выражений:

• \(8^{2} = 8 * 8 = 64\), число 8 является корнем второй степени из 64;
• \(0,6^{2} = 0,6 * 0,6 = 0,36\), число 0,6 является корнем второй степени из 0,36;
• \(1^{2} = 1 * 1 = 1\), число 1 представляет собой корень второй степени из числа 1.

Следует отметить, что существуют числа, для которых не представляется возможным определить равный этому числу квадрат, являющийся действительным числом. То есть не для всех чисел возможно найти действительное число, квадрат которого был бы равен данному числу.

Арифметический корень второй степени из числа a обозначается таким образом:

\(\sqrt{a}\)

Можно встретить следующее обозначение арифметического корня второй степени из числа а:\( \sqrt[2]{a}\). Однако, цифру 2 (показатель корня) не нужно прописывать. Знак арифметического корня также называют радикалом. Данные понятия являются синонимами, то есть обладают абсолютно одинаковым значением и употребляются в обоих вариантах. Число, которое стоит под знаком корня, является подкоренным числом. В том случае, когда под знаком корня заключено целое выражение, его называют подкоренным выражением.

Исходя из понятия арифметического корня, можно вывести следующую формулу для любого \(a\geq0\):

\((\sqrt{a})^{2}=a\)

\(\sqrt{a}\geq0\)

Число 3 в рассматриваемом случае является показателем корня. Число или выражение, которое стоит под знаком корня, называют подкоренным выражением.

В качестве примера можно рассмотреть следующие выражения:

• \(\sqrt[3]{3,5}\) является арифметическим корнем 3-й степени из 3,5 или кубическим корнем из 3,5;
• \(\sqrt[3]{x+5}\) является арифметическим корнем 3-й степени из \(х+5\) или кубическим корнем из  \( х+5.\)

 

Запись арифметического корня имеет следующий вид:

\((\sqrt[n]{a})^{n}=a\)

В качестве примеров можно привести следующие выражения:

• \(\sqrt[9]{1,2}\) представляет собой арифметический корень седьмой степени из числа 1,2, где 1,2 представляет собой подкоренное число, а 9 является показателем корня;
• \\(sqrt[6]{y^{2}+6}\) представляет собой арифметический корень шестой степени из числа \(y^{2}+6\), где \(y^{2}+6\) представляет собой подкоренное выражение, а 6 является показателем корня.

По определению арифметического корня \(n-ной\) степени, подкоренным выражением должно являться неотрицательное число или выражение. В том случае, когда в равенстве \((\sqrt[n]{a})^{n}=a\) обе части умножают на -1, в результате получаются две равносильные части равенства: \(-(\sqrt[n]{a})^{n}=-a\). Таким образом, для нечетных показателей арифметического корня можно записать следующее равенство:\( \.sqrt[n]{-a}=-\sqrt[n]{a}\)

Примеры решения

Задача 1

Задача 2

Задача 3

Задача 4

Задача 5

Задача 6

Задача 7

Нужно решить уравнение:

\(\sqrt[3]{9+\sqrt{80}} +\sqrt[3]{9-\sqrt{80}}\)

Решение:

Предположим, что:

\(A = \sqrt[3]{9+\sqrt{80}} +\sqrt[3]{9-\sqrt{80}}\)

Тогда:

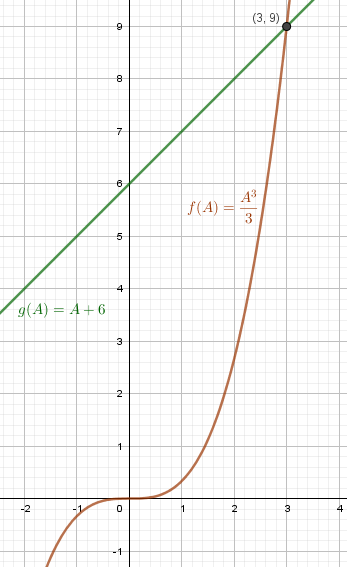
\(A^3 = \Biggl( \sqrt[3]{9+\sqrt{80}} +\sqrt[3]{9-\sqrt{80}} \Biggr)^3=\Biggl( \sqrt[3]{9+\sqrt{80}} \Biggr)^3+3 \Biggl(\sqrt[3]{9+\sqrt{80}} \Biggr)^2 \sqrt[3]{9-\sqrt{80}} +3 \sqrt[3]{9+\sqrt{80}} \Biggl( \sqrt[3]{9-\sqrt{80}} \Biggr)^2+ \Biggl( \sqrt[3]{9-\sqrt{80}} \Biggr)^3=9+\sqrt{80}+9-\sqrt{80}+3\sqrt[3]{(9+\sqrt{80})(9-\sqrt{80})} \Biggl( \underbrace{\sqrt[3]{9+\sqrt{80}} +\sqrt[3]{9-\sqrt{80}}}_{= A} \Biggr) =18+3 \underbrace{\sqrt[3]{9^2-80}}_{= 1} \cdot A = 18+3A = 3(A+6 \)

В результате вычислений получено уравнение:

\(A^3 = 3(A+6)\)

Данное равенство можно преобразовать:

\(\frac{A^3}{3} = A+6\)

Затем следует решить графически полученное уравнение:

\(A = 3 \)- искомое значение выражения

Ответ: 3