Как найти арккосинус: формула, свойства, функция

Получение функции arccos

Рассмотрим понятие функции \(y=\cos x\). Она обладает областью определения, в рамках которой, как и функция арксинуса, является кусочно-монотонной. По этой причине обратное соответствие, равное \(y=\arccos x,\) нельзя посчитать за функцию.

В данном случае целесообразно проанализировать интервал убывания функции, на котором она принимает все свои значения: \([0;\pi ]\). Данный отрезок характеризуется строго монотонным убыванием функции \(y=\cos x\), где она принимает все свои значения лишь однажды.

Таким образом, на отрезке \([0;\pi ]\) можно заметить обратную функцию \(y=\arccos x\). График этой обратной функции является симметричным графику \(y=\cos x\) на интервале \([0;\pi ]\) по отношению к первой прямой \(y=x\).

Свойства функции arccos

Функция arccos обладает следующими свойствами, которые можно использовать при математических и инженерных вычислениях. Данные свойства следует знать, чтобы решать задачи разной степени сложности:

1. \(\arccos(-x)=\pi -\arccos x\). Функция является центрально-симметричной по отношению к точке \(\left(0;{\frac {\pi }{2}}\right)\). Данную функцию определяют, как индифферентную, то есть не относят к четным или нечетным. Это является ответом на вопрос о четности функции.
2. \(\arccos x>0\), если при приведении обнаружено, что \(-1\leqslant x<1\).
3. \(\arccos x=0\) когда \(x=1\).
4. \(\arccos x={\frac {\pi }{2}}-\arcsin x\).
5. \(\arccos x=\left\{{\begin{matrix}\arcsin {\sqrt {1-x^{2}}},\qquad 0\leqslant x\leqslant 1\\\pi -\arcsin {\sqrt {1-x^{2}}},\qquad -1\leqslant x<0\end{matrix}}\right.\)
6. \(\arccos x=\operatorname {arcctg} {\frac {x}{\sqrt {1-x^{2}}}}\).
7. \(\arccos x=\left\{{\begin{matrix}\operatorname {arctg}\,{\frac {{\sqrt {1-x^{2}}}}{x}},\qquad 0<x\leqslant 1\\\pi +\operatorname {arctg}\,{\frac {{\sqrt {1-x^{2}}}}{x}},\qquad -1\leqslant x<0\end{matrix}}\right.\)
8. \(\arccos x=2\arcsin {\sqrt {\frac {1-x}{2}}}\).
9. \(\arccos x=2\arccos {\sqrt {\frac {1+x}{2}}}.\)
10. \(\arccos x=2\operatorname {arctg}{\sqrt {\frac {1-x}{1+x}}}\).

График функции \(y = arccosx\)

Функция y=\arccos x не прерывается и ограничивается на протяжении всей своей области определения. Данная функция строго убывает и не является отрицательной. Характеристики понятия функции arccos, которые используют при ее нахождении:

• \(\cos(\arccos x)=x, когда -1\leqslant x\leqslant 1 \) (от минус единицы до плюс единицы);
• \(\arccos(\cos y)=y, если 0\leqslant y\leqslant \pi ;\)
• \(D(\arccos x)=[-1;1]\) является областью определения;
• \(E(\arccos x)=[0;\pi ]\) является областью множества значений.

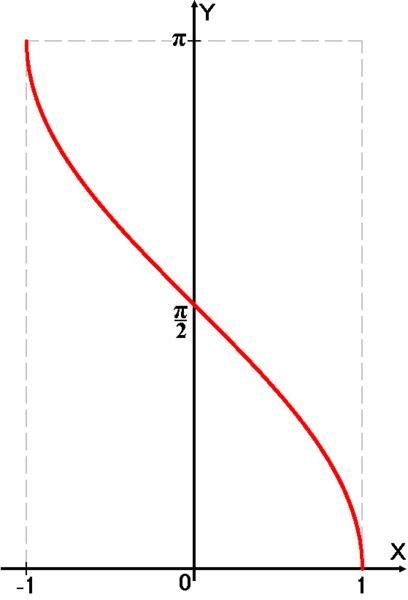
Функцию \(y=\arccos x\) можно изобразить графически. В результате нужный график принимает следующий вид:

Основное соотношение

При решении задач принято использовать главные соотношения в виде формул. К примеру, уравнения:

\(\arcsin x+\arccos x={\frac {\pi }{2}}\)

\(\operatorname {arctg}\,x+\operatorname {arcctg}\,x={\frac {\pi }{2}}\)