Центральный и вписанный угол в окружности
Что такое центральный и вписанный угол в окружности
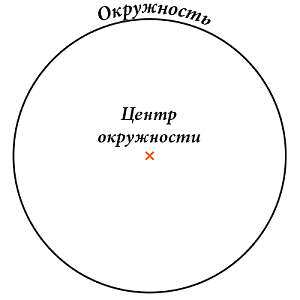
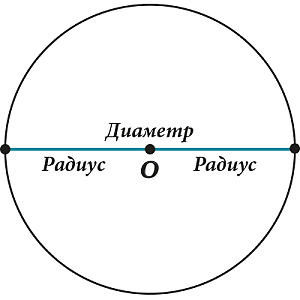
Центром окружности называют точку, которая равноудалена от всех других точек окружности.
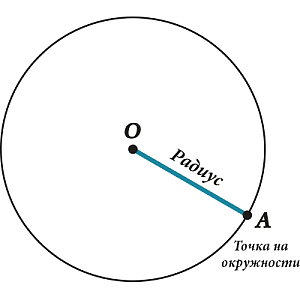
Радиус — является отрезком, который соединяет центр и точку на окружности.
Круг может обладать множеством радиусов, в соответствии с количеством точек, расположенных на рассматриваемой окружности. При этом все радиусы будут обладать одинаковой длиной. В некоторых случаях за радиус принимают длину отрезка, соединяющего центр с точкой окружности, а не сам отрезок.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
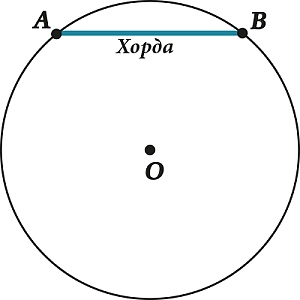
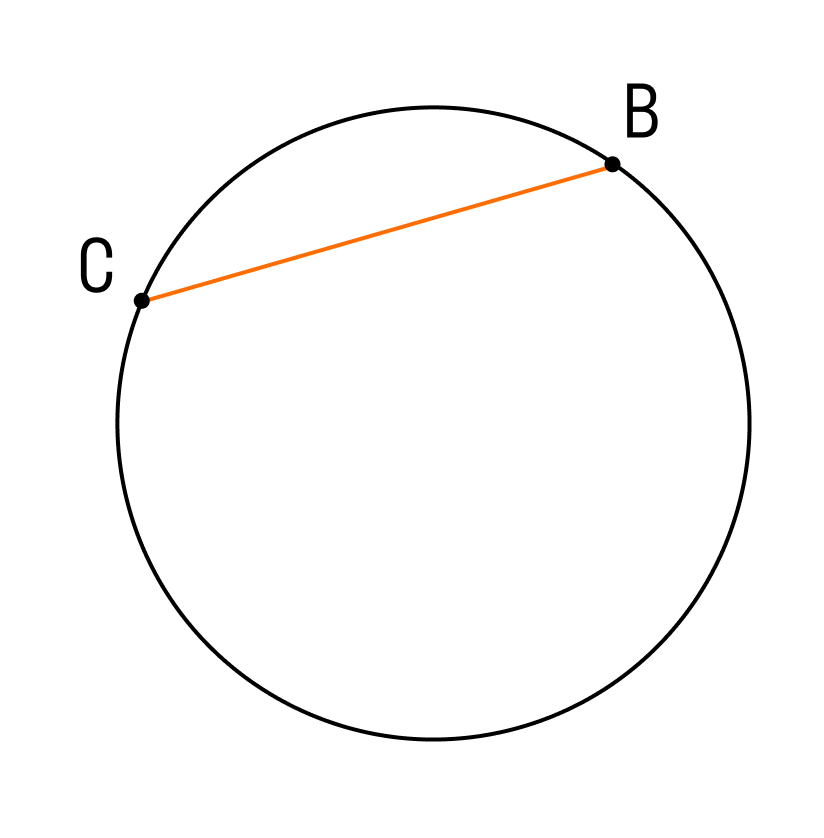
Когда отрезок соединяет пару точек, расположенных на окружности, его называют хордой.
Существует устоявшееся выражение: «хорда стягивает дугу». К примеру, хорда \displaystyle AB стягивает дугу \displaystyle AB.
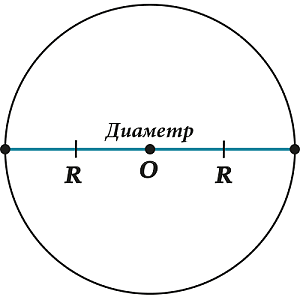
В том случае, когда хорда пересекает центр, она является диаметром.
Как правило, под диаметром подразумевают длину отрезка, который соединяет пару точек окружности и проходит через ее центр. Радиус составляет ½ диаметра.
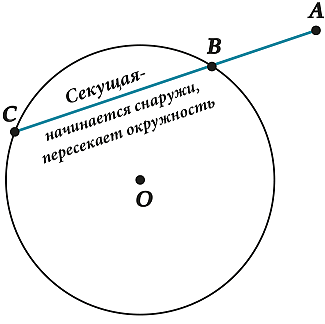
В окружности можно отметить не только хорды, но и секущие. С примером можно ознакомиться на рисунке:
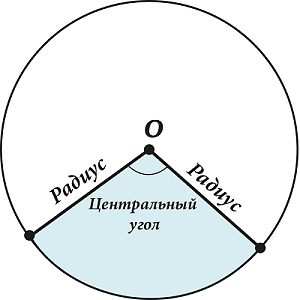
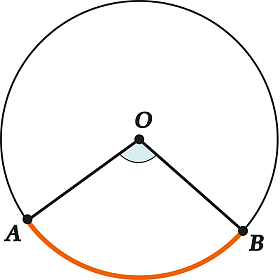
Центральный угол представляет собой угол, который расположен между двумя радиусами окружности.
Стороны, которые принадлежат центральному углу, выходят из центра окружности. В связи с этим, данный угол называют центральным.
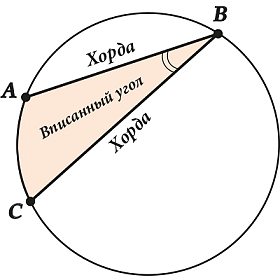
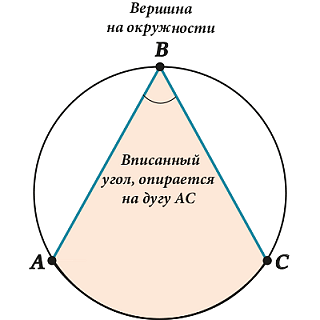
Вписанный угол является углом между парой хорд, пересекающихся в точке на окружности.
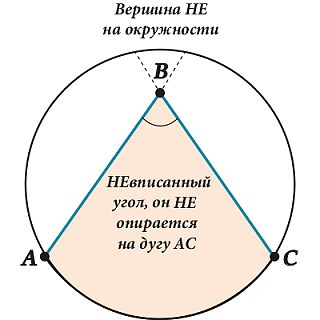
В данном случае вписанный угол \(\displaystyle ABC\) опирается на дугу (или на хорду) \(\displaystyle AC\). При этом не каждый угол, который расположен внутри окружности, является вписанным, а лишь тот, у которого вершина расположены на самой окружности.
В качестве единиц измерения дуг и углов используют градусы и радианы.
Градусной мерой или величиной дуги является величина, выраженная в градусах, соответствующего центрального угла.
На рисунке изображена пара дуг \(\displaystyle AB\) и два центральных угла. Большей дуге соответствует больший угол, несмотря на то, что он превышает \( \displaystyle 180{}^\circ\), а меньшей дуге соответствует меньший угол.
Радианы представляют собой способ измерения угла в радиусах, то есть угол, равный \(\displaystyle 1\) радиан является таким центральным углом, длина дуги которого равна радиусу окружности.
Выражать отношение длины окружности к радиусу не корректно в таких числах, как \(\displaystyle 1,\text{ }2,\text{ }3,\frac{7}{5},\frac{2}{239}\). Не допустимо говорить, что половина окружности в \(\displaystyle 2,5\) раза или в \(\displaystyle \sqrt{17}\) раз больше радиуса. В таком случае целесообразно использовать букву \(\displaystyle \pi\).
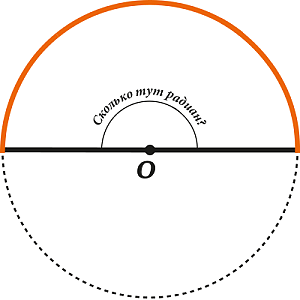
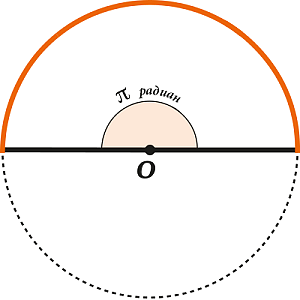
\( \pi\) является числом, которое выражает отношение длины полуокружности к радиусу.
Таким образом, развернутый угол составляет \( \pi\) радиан, так как половина окружности в \(\pi\) раз больше радиуса. Принято, что \(\displaystyle \pi \approx 3,14\).
Исходя из того, что развернутый угол равен \(\pi\) радиан, можно выразить любые углы в радианах.
\(\displaystyle 30{}^\circ \displaystyle \frac{\pi }{6}\)
\(\displaystyle 45{}^\circ \displaystyle \frac{\pi }{4}\)
\(\displaystyle 90{}^\circ \displaystyle \frac{\pi }{2}\)
\(\displaystyle 180{}^\circ \displaystyle \pi\)
\(\displaystyle 270{}^\circ \displaystyle \frac{3\pi }{2}\)
\(\displaystyle 360{}^\circ \displaystyle 2\pi\)
Свойства центральных и вписанных углов
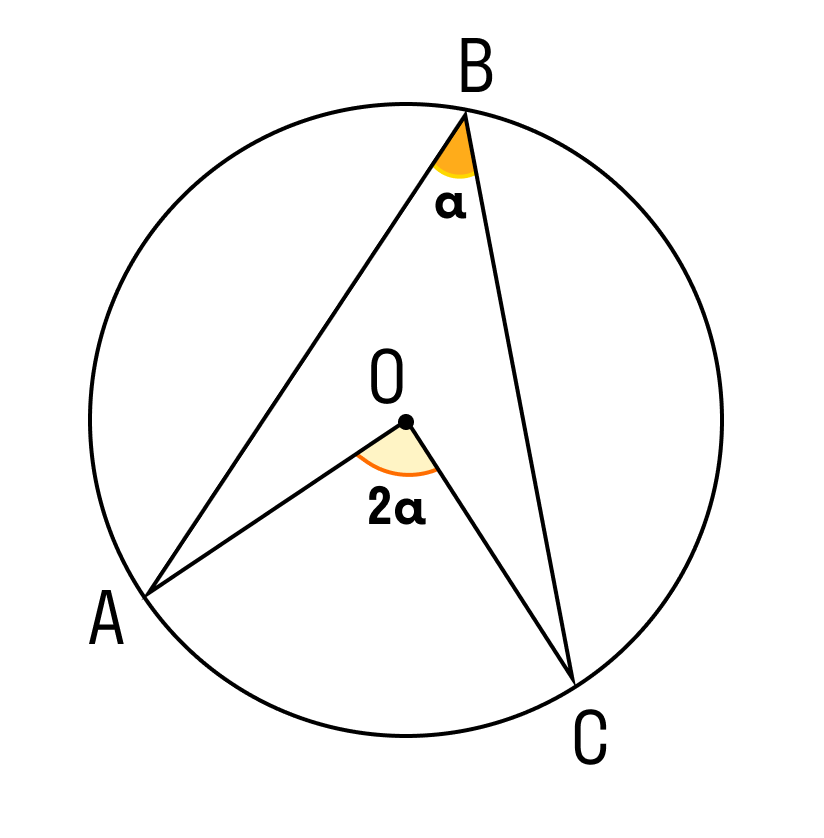
При решении задач по геометрии часто используют свойства центрального и вписанного углов. Например, вписанный угол в два раза меньше центрального угла в том случае, когда оба этих угла опираются на одну и ту же дугу.
Угол AOC и угол ABC, который вписан в круг, опираются на дугу AC. При этом центральный угол соответствует дуге AC, а угол ABC равен половине угла AOC.
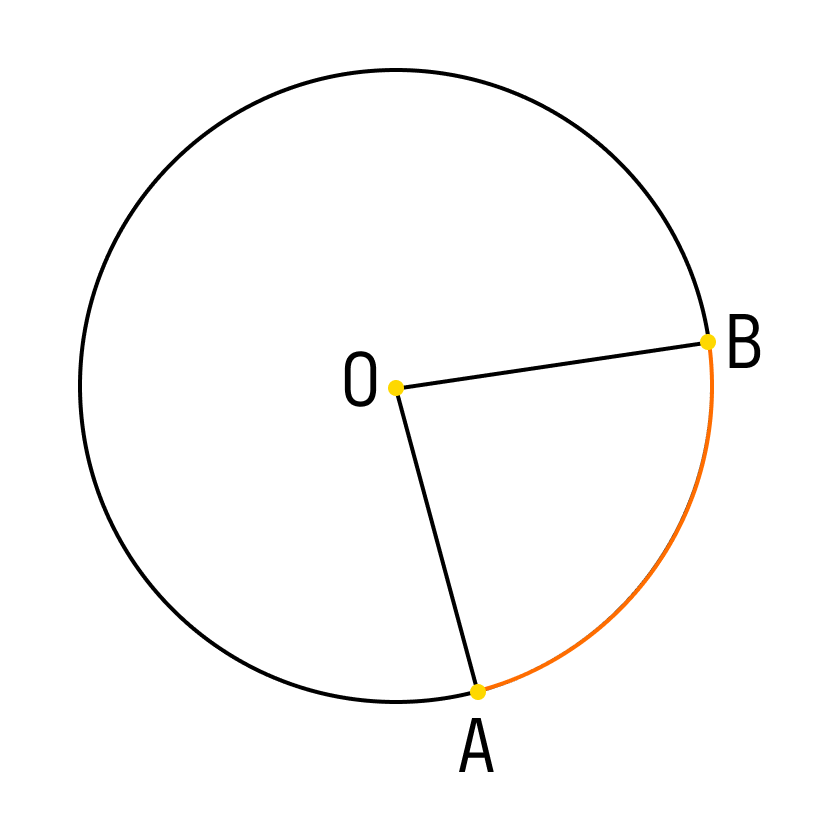
Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается.
На примере, угол АОВ равен дуге АВ.
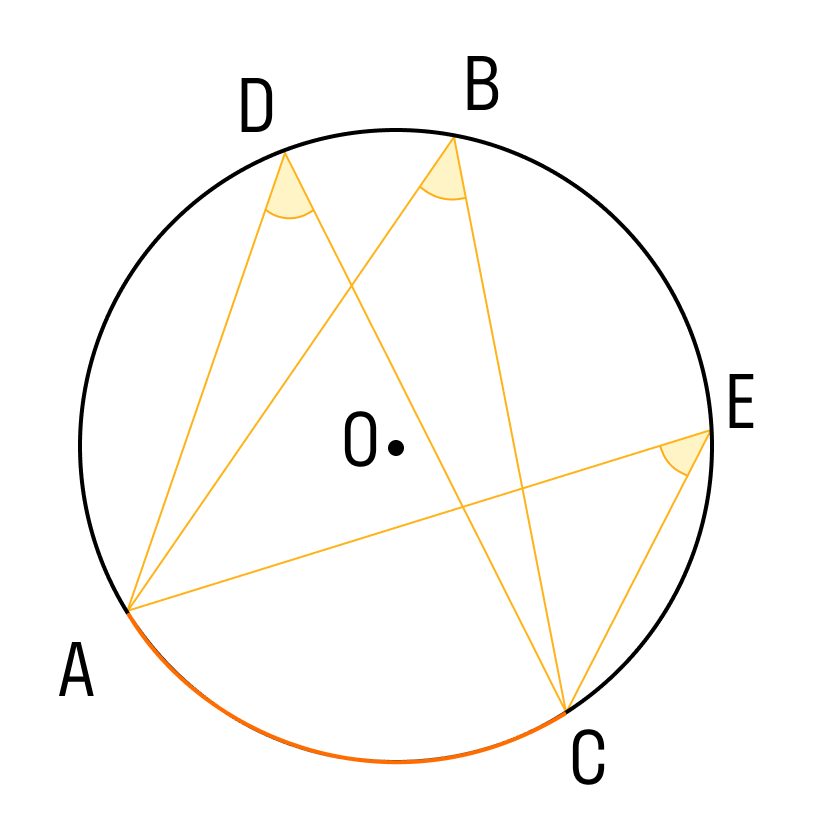
В том случае, когда в круг вписаны углы, опирающиеся на одну и ту же дугу, то такие углы будут равны.
На примере, угол ADC равен углу ABC и равен углу AEC, так как эти углы вписаны в окружность и опираются на одну и ту же дугу.
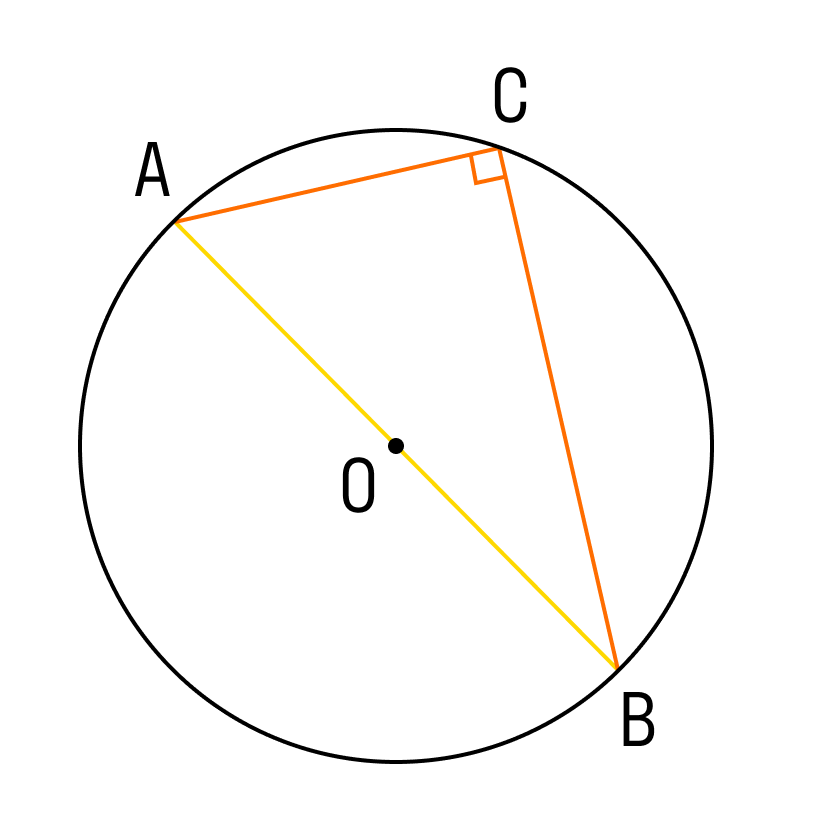
Если в окружность вписан угол, который опирается на ее диаметр, то такой угол является прямым.
К примеру, угол ACB опирается на диаметр и на дугу AB. При этом с помощью диаметра окружность делится на пару равных частей. Таким образом, дуга AB равна 180 градусов, а угол СAB составляет половину этой дуги, то есть равен 90 градусов.
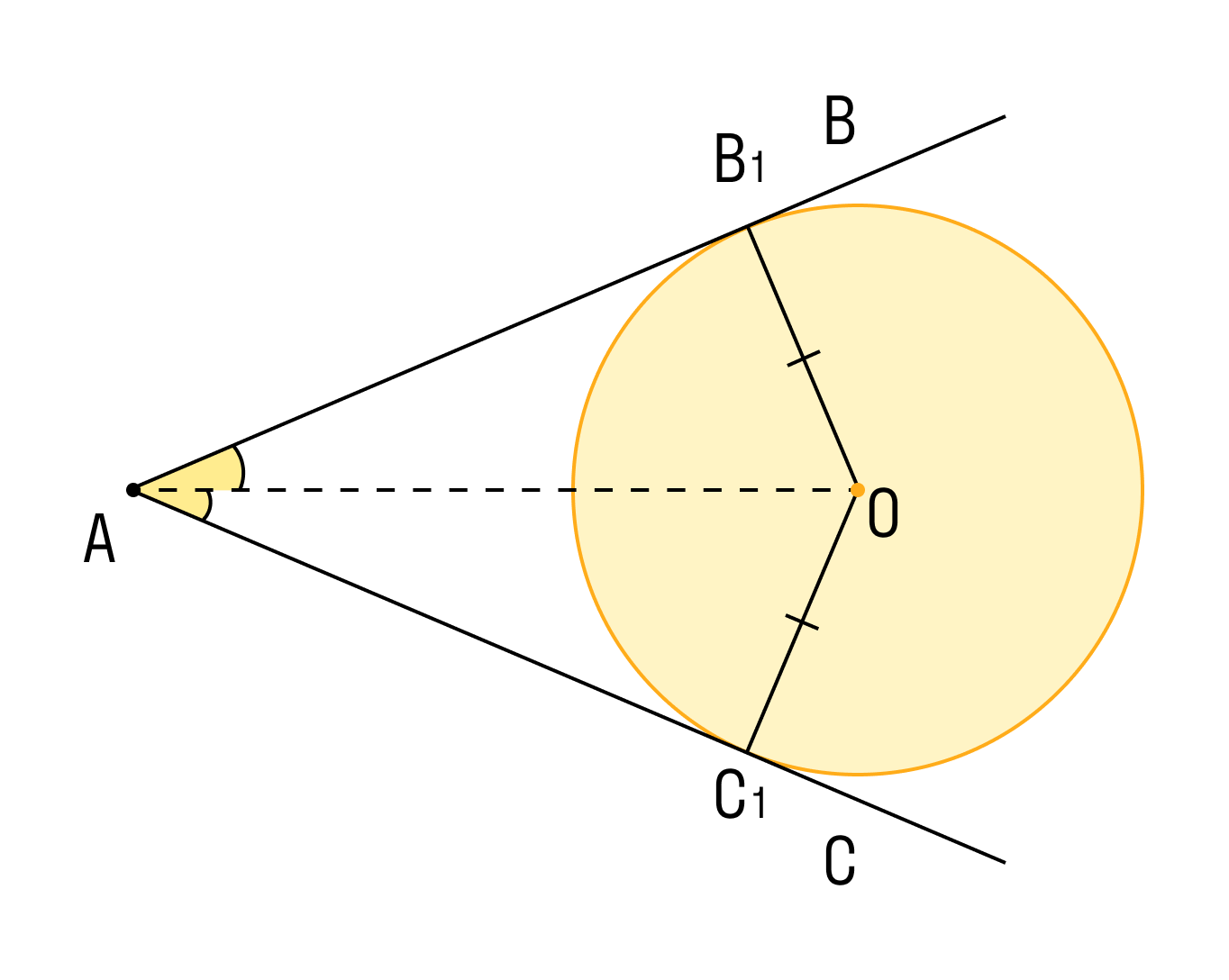
Описанный угол является углом, который образован двумя касательными к окружности.
К примеру, угол CAB, который образован двумя касательными к окружности, является описанным. В этом случае AO представляет собой биссектрису угла CAB. Таким образом, центр окружности расположен на биссектрисе описанного угла.
Градусная мера вписанного угла составляет половину градусной меры дуги, на которую он опирается, и равна половине градусной меры центрального угла, опирающегося на эту же дугу.
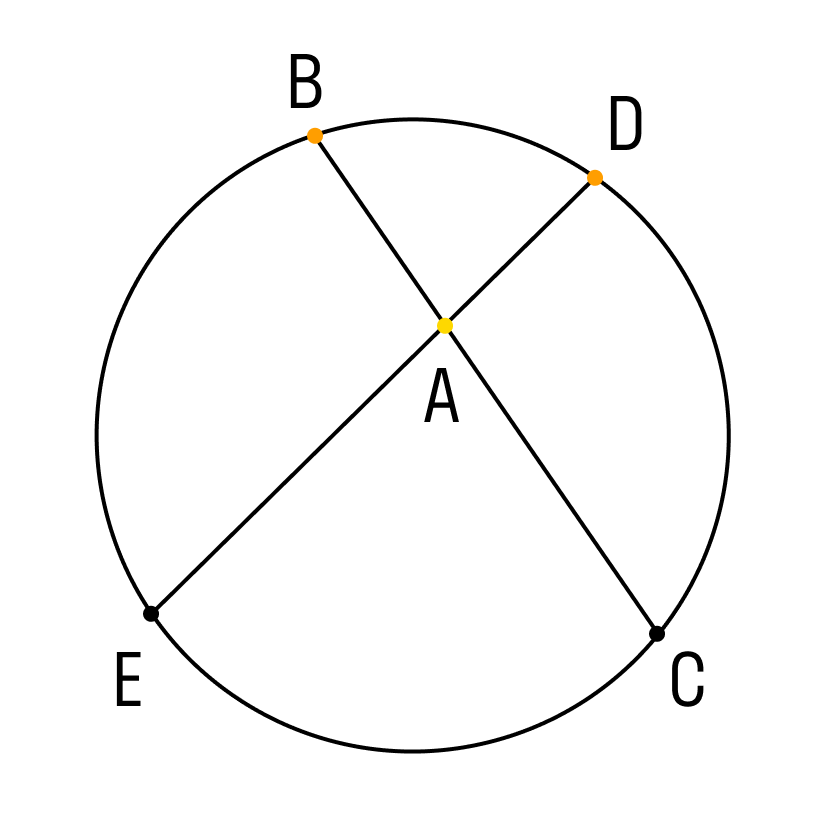
Хорда является отрезком, который соединяет пару точек круга. Когда две хорды в окружности имеют точку пересечения, произведения отрезков одной равно произведению отрезков другой.
Например, AB * AC = AE * AD
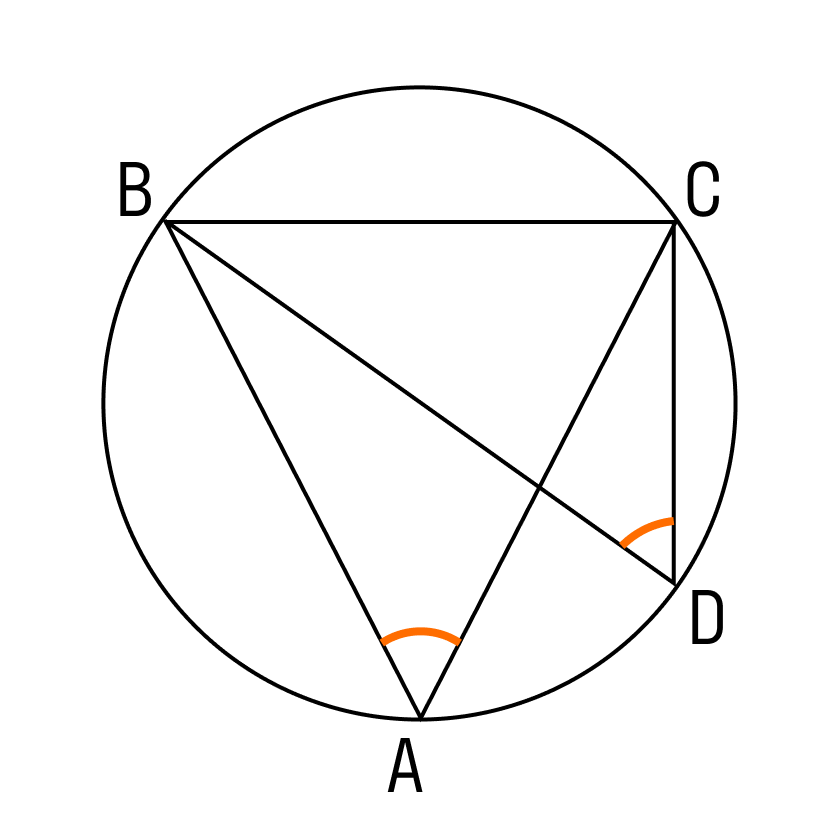
Таким образом, сторонами вписанного в окружность угла являются хорды. Если вписанные углы опираются на одну и ту же хорду, они равны при условии, что их вершины находятся по одну сторону от хорды.
К примеру, угол BAC равен углу CAB, так как данные углы расположены на хорде BC.
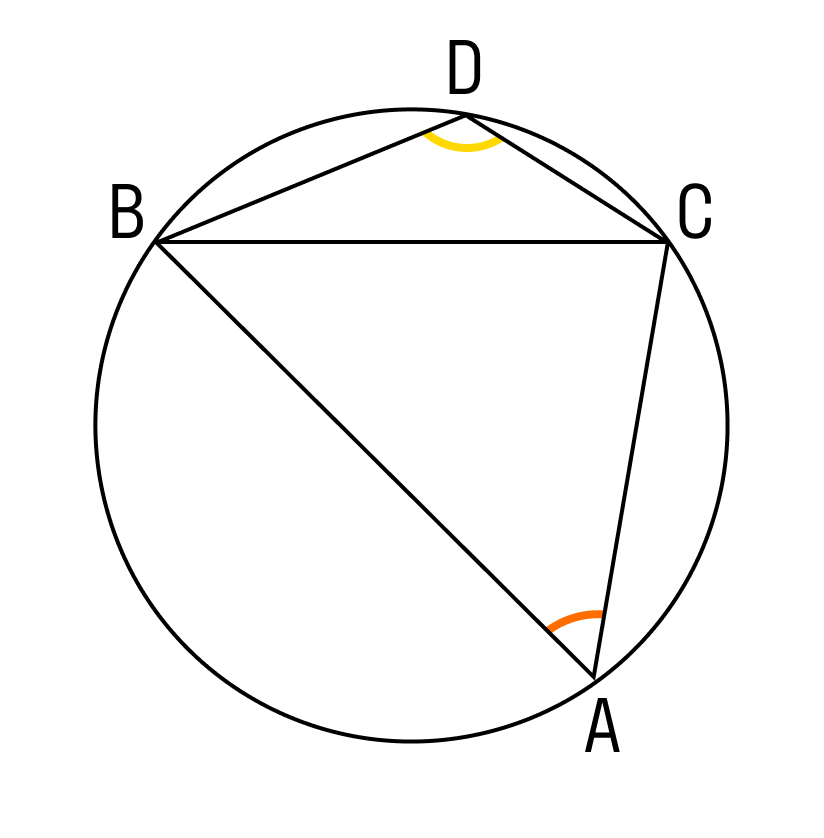
В том случае, когда пара вписанных углов опираются на одну и ту же хорду, их градусная мера в сумме составляет 180 градусов при условии, что их вершины находятся по разные стороны от хорды.
Например, сумма углов BAC и BDC составляет 180 градусов.
Доказательство теоремы
Существует определенная закономерность, которая связывает вписанный и центральный угол. Величина вписанного угла в два раза меньше величины соответствующего центрального угла.
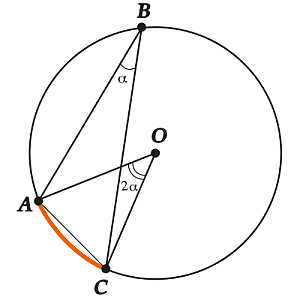
Соответствующим центральным углом называют такой, у которого концы совпадают с концами вписанного угла, а вершина — с центром окружности. Также соответствующий центральный угол «смотрит» на ту же хорду (\(\displaystyle AC\)), что и вписанный угол. Предположим, что какая-то из хорд пересекает центр окружности.
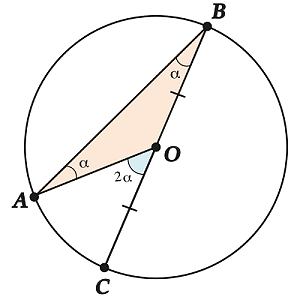
Геометрическая фигура \(\displaystyle \Delta AOB\) является равнобедренным треугольником, так как \(\displaystyle AO \ и \ \displaystyle OB\) представляют собой радиусы. Таким образом:
\(\displaystyle \angle A=\angle B\) (обозначили их \( \displaystyle \alpha\)).
\(\displaystyle \angle AOC\) является внешним углом для \(\displaystyle \Delta AOB\). Согласно свойству, внешний угол соответствует сумме двух внутренних углов, которые не являются с ним смежными:
\(\displaystyle \angle AOC=\angle A+\angle B\)
В результате:
\(\displaystyle \angle AOC\text{ }=\text{ }2\alpha\)
С другой стороны, \(\displaystyle \angle AOC\) является центральным углом для вписанного \( \angle ABC.\)
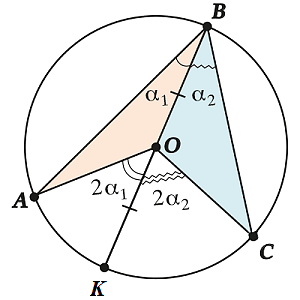
В данном случае получилось доказать, что центральный угол в два раза больше, чем вписанный. Однако, не всегда хорда \(\displaystyle BC\) пересекает центр окружности. Можно рассмотреть вторая вариант построения углов, когда центр окружности расположен внутри \(\displaystyle \angle ABC\).
Если провести диаметр окружности, то ситуация станет подобна первому случаю. В связи с этим, можно записать:
\(\displaystyle \angle ~AOK=2~\angle ~ABK\)
\(\displaystyle \angle ~COK=2~\angle CBK\)
С другой стороны:
\(\displaystyle \angle ~ABC=\angle ~ABK+~\angle ~CBK\)
\(\displaystyle \angle ~AOC=\angle ~AOK+~\angle ~COK\)
Таким образом:
\(\displaystyle \angle ~AOC=2~\angle ~ABC\)
На чертеже:
\(\displaystyle \angle ~ABC=~{{\alpha }_{1}}+{{\alpha }_{2}}\)
\(\displaystyle \angle ~AOC=2{{\alpha }_{1}}+2{{\alpha }_{2}}\)
Во втором случае теорема также доказана.
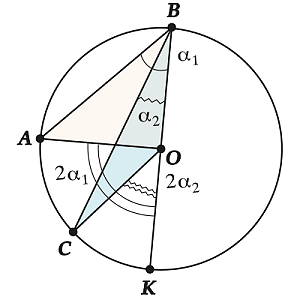
Можно смоделировать еще один вариант построения окружности и углов, при котором центр вне угла \(\displaystyle ABC\).
Порядок действий будет аналогичный. Необходимо построить диаметр, который пересекает точку \(\displaystyle \text{B}\). В данном случае вместо суммы используется разность:
\(\displaystyle \angle ~ABC=~{{\alpha }_{1}}-{{\alpha }_{2}}\)
\(\displaystyle \angle ~AOC=2{{\alpha }_{1}}-2{{\alpha }_{2}}\)
\(\displaystyle \angle ~AOC=2~\angle ~ABC\)
В результате теорема справедлива и в третьем варианте. Из утверждения можно сделать два важных вывода.
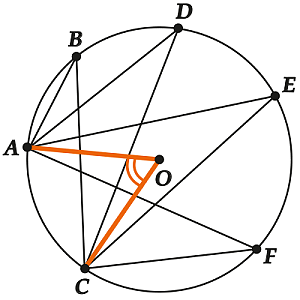
Все вписанные углы, которые опираются на одну дугу, равны между собой.
На рисунке изображена дуга \(\displaystyle AC\). Существует множество вписанных углов, которые на нее опираются. Данные углы могут отличаться, но, в любом случае, имеют одинаковый соответствующий центральный угол \(\displaystyle \angle ~AOC\). Можно сделать вывод, что все эти вписанные углы равны между собой.
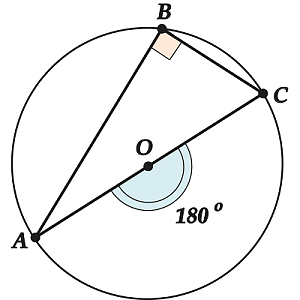
Угол, который опирается на диаметр окружности, является прямым.
Центральным для вписанного угла \(\displaystyle \angle ABC\) является угол \(\displaystyle \angle ~AOC\), который составляет \(\displaystyle 180{}^\circ\). Таким образом, \(\displaystyle \angle ~ABC\) и все вписанные углы, опирающиеся на \(\displaystyle AC\) равны \(\displaystyle 90{}^\circ.\)
Примеры решения задач
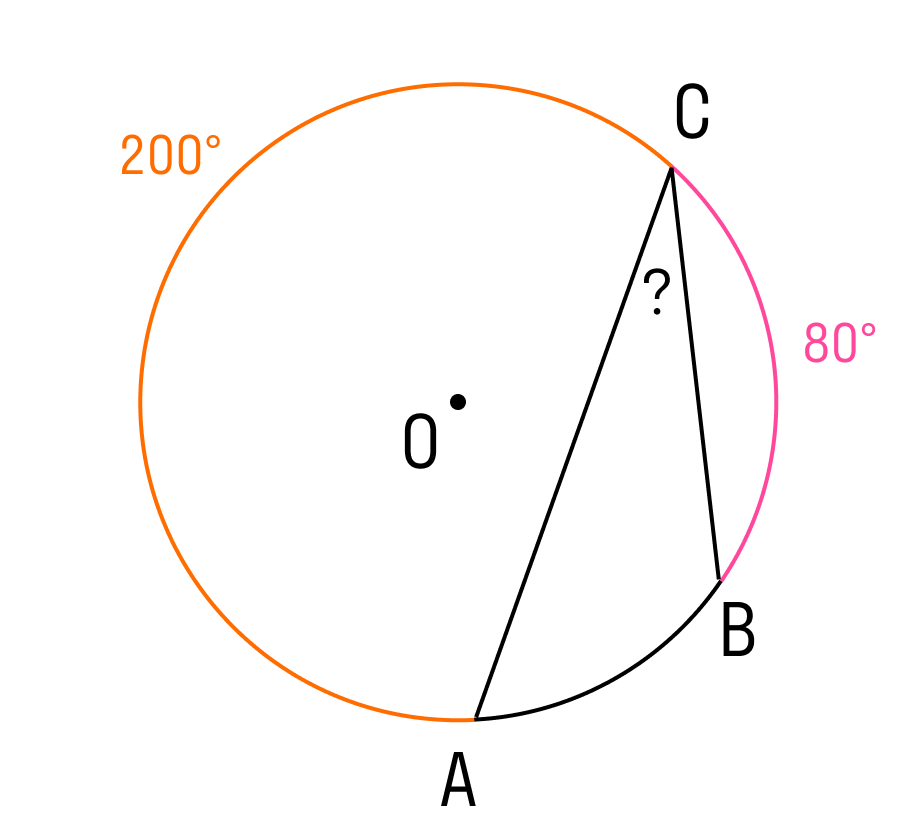
Имеется некая окружность, в которой дуга, имеющая обозначение AC, равна\( \displaystyle 200{}^\circ\), дуга BC составляет \(\displaystyle 80{}^\circ\). Необходимо вычислить величину вписанного угла, опирающегося на дугу АВ.
Решение:
Окружность составляет \(\displaystyle 360{}^\circ\). Для того чтобы найти дугу АВ, требуется:
\(\displaystyle 360{}^\circ - AC - CB = 360 - 200 - 80 = 80\)
Согласно теореме о вписанном угле, его величина равна половине дуги, на которую он опирается. Таким образом:
\(АCB = ½ AB = \displaystyle 40{}^\circ\)
Ответ: угол АСВ равен \(\displaystyle 40{}^\circ\)
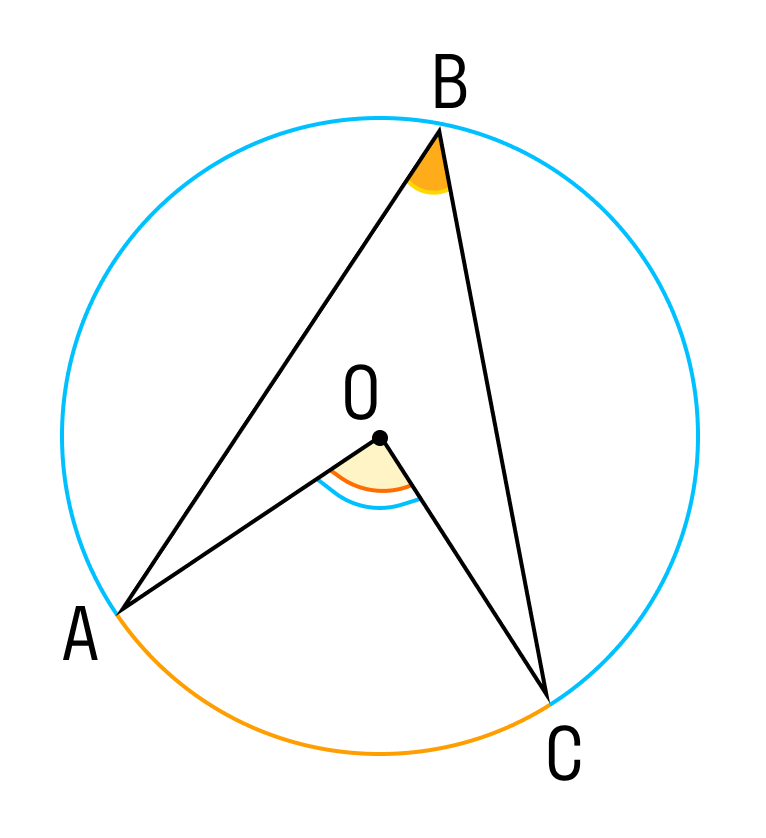
Дана окружность. Угол АOC составляет\( \displaystyle 140{}^\circ\). Необходим определить величину вписанного угла.
Решение:
На рисунке видно, что в окружности расположен центральный угол и дуга AC, которая равна \(\displaystyle 140{}^\circ\). Исходя из теоремы о вписанном и центральном углах, вписанный угол составляет половину центрального. Можно записать формулу:
\(ABC = ½ AC = 140/2 = \displaystyle 70{}^\circ\)
Ответ: угол ABC равен \(\displaystyle 70{}^\circ\).
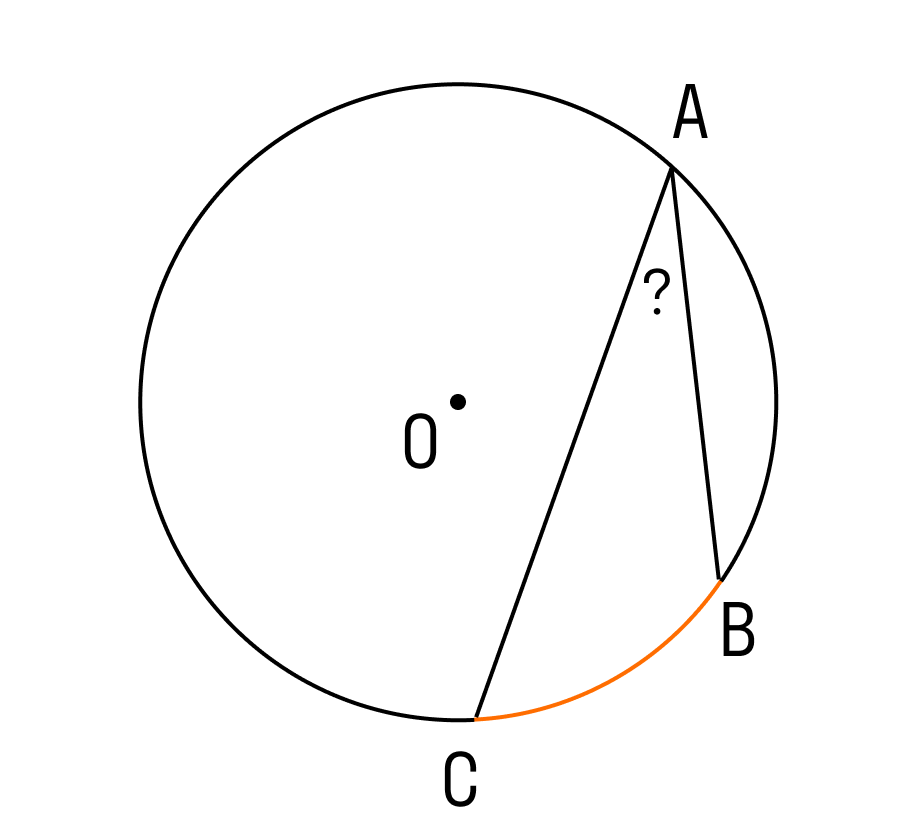
Необходимо вычислить величину вписанного в окружность угла, который опирается на дугу. При этом дуга составляет 1/5 окружности.
Известно, что окружность равна \(\displaystyle 360{}^\circ\). Таким образом:
\(СB = ⅕ \ от \ 360 = \displaystyle 72{}^\circ\)
Согласно теореме о вписанном угле, он составляет половину дуги, на которую опирается:
\(CAB = ½\) от \(CB = 72/36 = \displaystyle 36{}^\circ\)
Ответ: угол САВ равен \(\displaystyle 36{}^\circ\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так