Диаграммы Эйлера-Венна
Что такое диаграммы Эйлера-Венна
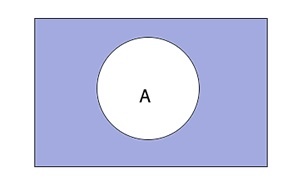
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.
Для отражения отношений между множествами математики Джон Венн и Леонард Эйлер использовали для способа. Если Венн использовал для обозначения множеств замкнутые фигуры, то Эйлер использовал круги.
Диаграммы Эйлера-Венна являются важным частным случаем кругов Эйлера. Диаграммы изображают все 2^n комбинаций n свойств, что является конечной булевой алгеброй. В случае n = 3 диаграмма Эйлера-Венна обычно состоит из трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приближенно равным длине стороны треугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Принцип построения
Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.
Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.
С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:
- В первую очередь необходимо начертить диаграмму, заштриховав все множества, находящиеся в левой части равенства.
- Следующим шагом будет начертание другой диаграммы и штриховка всех множеств, которые находятся в правой части равенства.
- В случае, когда на диаграммах заштрихована одна и та же область, торжество истинно.
Дополнение множества
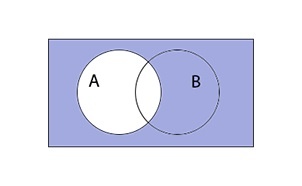
Дополнением к множеству A является множество \(\overline A\), которое состоит из элементов, не входящих в А.
\(\overline A\;=\;\left\{x\;\vert\;x\;\not\in\;A\right\}\)
При этом не все элементы, не являющиеся элементами А, могут быть включены в \(\overline A.\) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение \overline A определяется следующим образом:
\(\overline A\;=\;U\;\backslash\;A\)
Таким образом выглядит дополнение \(\overline A\) графически:
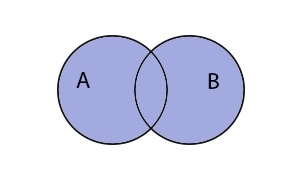
Объединение множеств
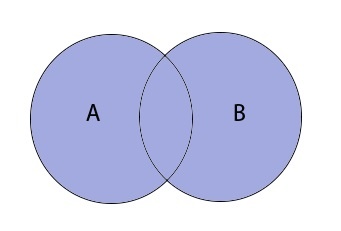
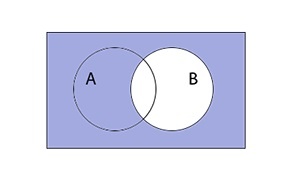
Объединением множеств A и B называют множество \(A\;\cup\;B\), которое состоит из элементов, принадлежащих хотя бы одному из множеств.
Объединение записывается следующим образом:
\(A\;\cup\;B\;=\;\left\{x\;\vert\;x\;\in\;A\;или\;x\;\in\:B\right\}\)
Таким образом объединение множеств выглядит графически:
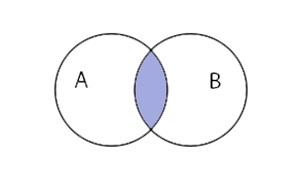
Пересечение множеств
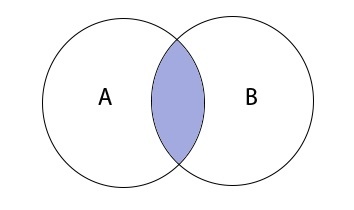
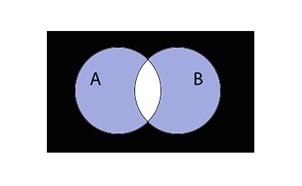
Пересечением множеств A и B является множество \(A\;\cap\;B\), которое состоит из элементов, входящих в оба множества.
Пересечение множеств записывается следующим образом:
\(A\;\cap\;B\;=\;\left\{x\;\vert\;x\;\in\;A\;и\;x\;\in\;B\right\}\)
Таким образом пересечение множеств выглядит графически:
Симметричная разность множеств
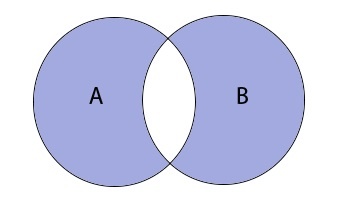
Симметричная разность A \ B — это такое множество, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество
Разность множеств записывается следующим образом:
\(A\bigtriangleup B=(A\backslash B)\cup(B\backslash A)\)
Таким образом разность выглядит графически:
Разность множеств
Разностью A \ B является множество элементов A, не входящих в B.
Разность множеств записывается следующим образом:
\(A\;\backslash\;B\;=\;\left\{x\;\vert\;x\;\in\;A\;и\;x\;\not\in\;B\right\}\)
Таким образом разность выглядит графически:
Использование диаграмм Эйлера-Венна для доказательства логических равенств
Рассмотрим, как диаграммы Эйлера-Венна применяются для доказательства логических равенств.
Предположим, что перед нами конъюнкция множеств \(A\;\wedge\;B\)
В первую очередь обратим внимание на левую часть равенства. Построим диаграмму для множеств А и B. Графически отметим дизъюнкцию, заштриховав оба круга цветом.
Теперь отобразим инверсию, заштриховав область за пределами множеств.
Обратим внимание на правую часть равенства. В первую очередь отобразим инверсию A штриховкой область за пределами круга множества A цветом.
Проведем аналогичную операцию с множеством B.
Теперь штриховкой черным цветом всех областей пересечения отобразим конъюнкцию инверсий множеств А и B.
При сравнении области для отображения правой и левой частей, становится очевидно, что они равны. Справедливость логического равенства доказана с помощью диаграммы Эйлера-Венна.
Примеры задач с решением
Задача
Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?
Решение
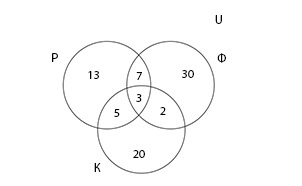
В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.
\(n(U)\;=\;100\\n(Р)\;=\;28,\;n(Ф)\;=\;42,\;n(К)\;=\;30\\n\;(Р\;\cap\;Ф)\;=\;10,\;n(Р\;\cap\;К)\;=\;8,\;n\;(Ф\;\cap\;К)\;=\;5\\n\;(Р\;\cap\;Ф\;\cap\;К)\;=\;3\)
Необходимо найти \(n(Р\;\cup\;Ф\;\cup\;К)\;=\;n\;(U\;\backslash\;(Р\;\cap\;Ф\;\cap\:К))\)
В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна. Составляя ее, важно помнить, что если в \(Р\;\cap\;Ф\;\cap\:К\) три элемента, а в множестве \(Р\;\cap\;Ф\) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено.
Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.
\(n(Р\;\cup\;Ф\;\cup\;К)\;=\;13\;+\;7\;+\;30\;+5\;+\;3\;+\;2\:+\;20\;=\;80\)
Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:
\(n(U\;\backslash\;(Р\;\cup\;Ф\;\cup\;К))\;=\;100\;-\;80\;=\;20\)
Ответ: 20 туристов не побывали ни в одном из указанных заведений.
Задача
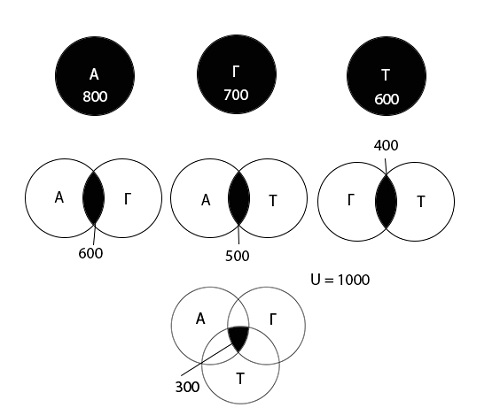
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?
Решение
Начнем с определения множеств и введения обозначений. В данном случае, их три:
- множество задач по алгебре («А»);
- множество задач по геометрии («Г»);
- множество задач по тригонометрии («Т»).
Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.
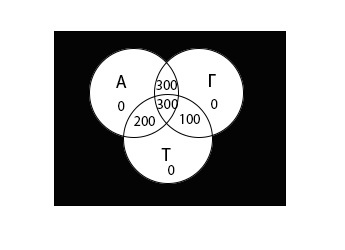
Теперь используя диаграмму, обозначим область, которую необходимо найти:
Определим количество школьников для всех возможных областей.
Обозначим искомую область А = 0, Г = 0, Т = 0 как «х».
Найдем остальные области:
- Область А = 0, Г = 0, Т = 1: школьников нет.
- Область А = 0, Г = 1, Т = 0: школьников нет.
- Область А = 0, Г = 1, Т = 1: 100 школьников.
- Область А = 1, Г = 0, Т = 0: школьников нет.
- Область А = 1, Г = 0, Т = 1: 200 школьников.
- Область А = 1, Г = 1, Т = 0: 300 школьников.
- Область А = 1, Г = 1, Т = 1: 300 школьников.
Теперь внесем значения всех областей в диаграмму:
Определим x:
\(x\;=\;U\;-\;(A\;\cup\;Г\;\cup\;Т)\;\)
При U — универсум
U = 1000
\((A\;\cup\;Г\;\cup\;Т)\;=\; 0 + 0 + 0 + 300 + 300 + 200 + 100 = 900\)
x = 1000 - 900 = 100
Ответ: 100 школьников не решило ни одной задачи.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так