Как найти двугранный угол
Что такое двугранный угол
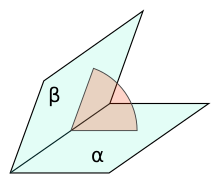
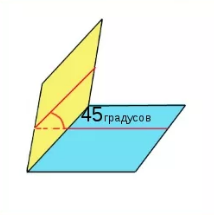
Двугранным углом называют геометрическую фигуру, которая сформирована парой полуплоскостей, выходящие из общей прямой.
Заметим, что угол, измеряемый в градусах, разделяющий пару плоскостей, является минимальным из количества двугранных углов, которые сформированы в результате пересечения плоскостей.
Важно отметить, что по модели двугранный угол может быть острым и тупым. При этом угол, разделяющий две плоскости, является острым. Это необходимо учитывать в решении задач, чтобы избежать путаницы.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: ru.wikipedia.org
Как найти
В поиске ответов на различные примеры из геометрии следует руководствоваться основными понятиями. Введем несколько обозначений для элементов двугранного угла.
Грани двугранного угла представляют собой полуплоскости, которые образовали данный угол.
Ребро двугранного угла является единой прямой для рассматриваемых полуплоскостей.
В процессе измерения двугранных углов используют величины линейных углов, то есть тех, что образованы при пересечении двугранного угла и плоскости, расположенной под прямым углом к ребру рассматриваемого угла. В результате для поиска величины двугранного угла рекомендуется следовать следующему алгоритму действий:
- следует определить какую-либо точку на его ребре;
- далее под прямым углом к ребру нужно опустить из определенной ранее точки лучи ко всем граням;
- угол, который разделяет изображенные лучи, соответствует величине искомого двугранного угла.
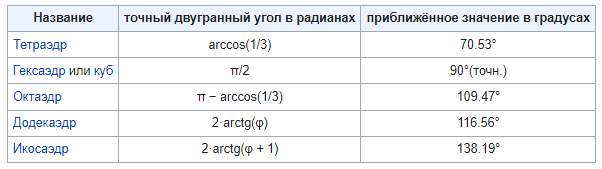
Запишем в табличной форме значения двугранных углов, характерные для правильных многогранников:
В данном случае следует считать \(\phi\) равным \(\frac{1+\sqrt{5}}{2}\), то есть золотым сечением.
Виды двугранных углов
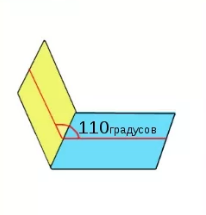
Тупой двугранный угол представляет собой такой угол, градусная величина которого превышает значение в 90°.
Тупой двугранный угол:
Источник: rusinfo.info
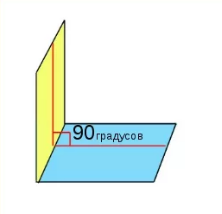
Прямой двугранный угол является таким двугранным углом, градусная мера которого соответствует 90°.
Прямой двугранный угол:
Источник: rusinfo.info
Острым двугранным углом называют двугранный угол с градусной мерой, равной 90°.
Острый двугранный угол:
Источник: rusinfo.info
Задачи
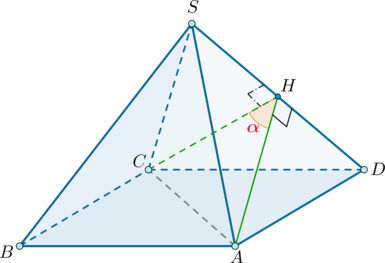
Имеется геометрическая фигура в виде пирамиды с четырьмя углами и равными между собой ребрами. При этом в основании фигуры расположен квадрат. Требуется определить, чему равен \(6\cos \alpha\) , если за \(\alpha\) обозначен угол, разделяющий смежные боковые грани.
Решение
Предположим, что искомая пирамида имеет следующее название SABCD. Пусть S играет роль вершины геометрической фигуры, а ее ребра соответствуют а. Тогда, согласно условию задания, требуется найти угол, разделяющий грани SAD и SCD.
Источник: shkolkovo.net
Построим \(CH\perp SD\). Заметим, что:
\(\triangle SAD=\triangle SCD\)
В этом случае AH также играет роль высоты в \(\triangle SAD\). Таким образом, исходя из определения:
\(\angle AHC=\alpha\)
Заметим, что \(\alpha\) является линейным углом, разделяющим грани SAD и SCD. При условии квадратного основания в пирамиде запишем следующее:
\(AC=a\sqrt2\)
Кроме того, имеет место такое равенство:
CH=AH
Высота AH находится в треугольнике с одинаковыми сторонами, равными а. Таким образом:
\(CH=AH=\frac{\sqrt3}2a\)
Воспользуемся теоремой косинусов применительно к \(\triangle AHC\):
\(\cos \alpha=\dfrac{CH^2+AH^2-AC^2}{2CH\cdot AH} =-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\)
Ответ: -2.
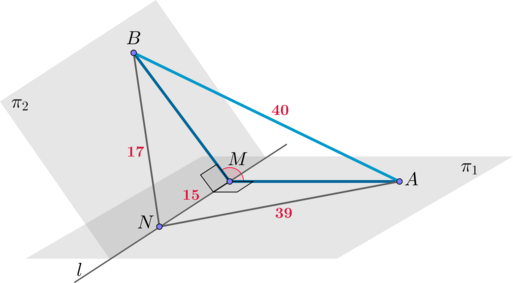
На рисунке изображено пересечение плоскостей, обозначенных за \(\pi_1\) и \(\pi_2\). В результате образуется общая прямая l с точками M и N. Полученные отрезки MA и MB расположены перпендикулярно по отношению к прямой l, а также принадлежат плоскостям за \(\pi_1\) и \( \pi_2\) соответственно. При этом справедливы следующие равенства: MN = 15; AN = 39; BN = 17; AB = 40. Необходимо вычислить \(3\cos\alpha\) , где \(\alpha\) является углом, разделяющим плоскости \(\pi_1\) и \(\pi_2\) .
Решение
Источник: shkolkovo.net
Заметим, что треугольник AMN обладает прямым углом, тогда:
\(AN^2 = AM^2 + MN^2\)
В результате:
\(AM^2 = 39^2 - 15^2 = 36^2\)
Прямоугольным также является треугольник BMN. В таком случае:
\(BN^2 = BM^2 + MN^2\)
Исходя из этого, получим:
\(BM^2 = 17^2 - 15^2 = 8^2\)
Воспользуемся теоремой косинусов применительно к треугольнику AMB:
\(AB^2 = AM^2 + MB^2 - 2\cdot AM\cdot MB\cdot\cos\angle AMB\)
Таким образом:
\(40^2 = 36^2 + 8^2 - 2\cdot 36\cdot 8\cdot\cos\angle AMB\qquad\Leftrightarrow\qquad \cos\angle AMB = -\dfrac{5}{12}\)
Исходя из того, что угол \(\alpha\), разделяющий плоскости, является острым, а угол \(\angle AMB\) определяется как тупой, получим следующее равенство:
\(\cos\alpha=\dfrac5{12}\)
\(3\cos\alpha = \dfrac54=1,25\)
Ответ: 1,25.
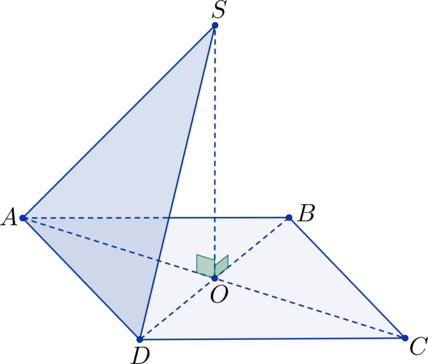
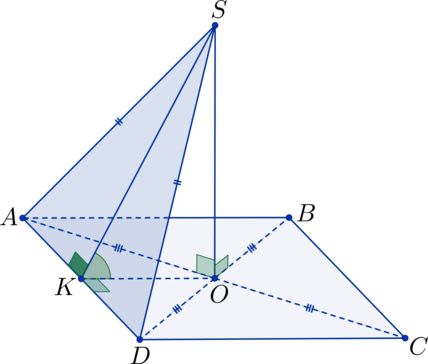
На рисунке изображен квадрат ABCD. В точке О пересекаются диагонали. Точка S расположена за пределами квадратной плоскости, а \(SO \perp ABC\). Требуется вычислить угол, разделяющий плоскости ASD и ABC, при условии, что SO = 5, а AB = 10.
Решение
Источник: shkolkovo.net
Геометрические фигуры в виде треугольников с прямыми углами \(\triangle SAO\) и \(\triangle SDO\) являются идентичными, согласно паре сторон и углу, который их разделяет:
\(SO \perp ABC \Rightarrow \angle SOA = \angle SOD = 90^\circ\)
AO = DO
Записанные выше равенства являются справедливыми, так как в точке O пересекаются диагонали квадрата, а SO служит общей стороной.
\(\Rightarrow AS = SD \Rightarrow \triangle ASD\)
\(\triangle ASD\) является равнобедренным. Точка K делит пополам AD. В таком случае SK представляет собой высоту в треугольнике \(\triangle ASD\), а OK обозначает высоту в треугольнике AOD. Таким образом, плоскость SOK расположена под прямым углом к плоскостям ASD и ABC. Можно сделать вывод о том, что \(\angle SKO\) является линейным углом, который соответствует искомому двугранному углу.
Источник: shkolkovo.net
Рассмотрим треугольник \(\triangle SKO\):
\(OK = \frac{1}{2}\cdot AB = \frac{1}{2}\cdot 10 = 5 = SO\)
Таким образом, \(\triangle SOK\) является равнобедренным прямоугольным треугольником. Тогда:
\(\angle SKO = 45^\circ.\)
Ответ: \(45^\circ.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так