Графики функций и их формулы
Что такое график функции
График функции — это визуальное представление зависимости между входными и выходными данными функции. График позволяет наглядно увидеть, как изменяются значения функции в зависимости от изменений в её аргументах.
На плоскости он представляется как набор точек, координаты которых соответствуют аргументам и значениям функции. Горизонтальная ось обычно представляет собой ось аргументов (независимой переменной), а вертикальная ось — ось значений функции (зависимой переменной).
График функции может иметь различные формы, такие как прямые линии, параболы, гиперболы, экспоненциальные кривые и другие. Визуальное представление графика позволяет легче анализировать поведение функции, находить экстремумы (минимумы и максимумы), определять интервалы возрастания и убывания, а также делать выводы о её свойствах. Играют важную роль в математике, науках, инженерии и других областях, где требуется анализировать и визуализировать зависимости между переменными.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Декарт вводит свою систему координат — способ представления точек на плоскости с помощью пар вещественных чисел.
Какие бывают
Графики функций могут быть классифицированы по различным критериям. Вот некоторые общие классификации:
-
По форме:
- прямая линия (линейная функция);
- парабола (квадратичная функция);
- гипербола (рациональная функция);
- экспоненциальная кривая (экспоненциальная функция);
- логарифмическая кривая (логарифмическая функция);
- тригонометрические кривые (синусоиды, косинусоиды и др.).
-
По поведению:
- функции возрастания и убывания;
- монотонные функции (всегда убывающие или возрастающие);
- ограниченные функции (ограниченные сверху или снизу);
- функции с экстремумами (минимумы и максимумы);
- функции с точками перегиба.
-
По периодичности:
- периодические функции (функции, которые повторяются через определенные интервалы).
-
По асимптотам:
- функции с горизонтальными или вертикальными асимптотами.
-
По числу аргументов:
- одномерные функции (зависят от одного аргумента);
- многомерные функции (зависят от нескольких аргументов).
-
По типу переменных:
- действительные функции (работают с действительными числами);
- комплексные функции (работают с комплексными числами).
-
По области определения и значений:
- определенные функции (имеют определение для всех возможных значений аргумента);
- частично определенные функции (имеют ограниченную область определения).
Формулы
Вот некоторые примеры функций вместе с их формулами:
-
Линейная функция: Формула: f(x)=ax+b, где a — коэффициент наклона, b — свободный член.
-
Квадратичная функция: Формула: f(x)=ax2+bx+c, где a, b и c — коэффициенты.
-
Экспоненциальная функция: Формула: f(x)=a⋅ebx, где a и b — коэффициенты, e — число Эйлера (примерно 2.71828).
-
Логарифмическая функция: Формула: f(x)=a⋅ln(bx), где a и b — коэффициенты, ln — натуральный логарифм.
-
Синусоидальная функция (синус или косинус): Формула: f(x)=A⋅sin(bx+c) или f(x)=A⋅cos(bx+c), где A — амплитуда, b — коэффициент частоты, c — смещение.
-
Параболическая функция: Формула: f(x)=ax2+bx+c, аналогичная квадратичной функции.
-
Гиперболическая функция: Пример: f(x)=xa, где a — коэффициент.
-
Полиномиальная функция: Пример: f(x)=anxn+an−1xn−1+…+a1x+a0, где ai — коэффициенты, n — степень полинома.
Как построить
Построение графиков функций — это процесс построения графика (кривой) соответствующей функции. Построение графиков базовых функций, таких как линейная, квадратичная, кубическая и т.д., довольно просто, а построение графиков сложных функций, таких как рациональная, логарифмическая и т.д., требует определенных навыков и понимания некоторых математических понятий.
Графиком функции f называется множество всех точек на плоскости вида (x, f(x)). График функции f можно также определить как график уравнения y = f(x). Таким образом, график функции является частным случаем графика уравнения.
При построении графиков функций мы выполняем следующие действия:
- Найдите область действия функции.
- Найдите и постройте графики x- и y-пересечений.
- Найдите асимптоты по вертикали, горизонтали и наклону и проведите пунктирные линии, чтобы разбить график вдоль этих линий и убедиться, что график не касается их.
- Создайте таблицу значений, взяв несколько произвольных значений x (по обе стороны от x-интерцепта и по обе стороны от вертикальной асимптоты) и вычислив соответствующие значения y.
- Постройте точки из таблицы и соедините их с помощью асимптот, области и диапазона.
Основная концепция построения графиков функций заключается в следующем:
- Если возможно, определите форму. Если это линейная функция вида f(x) = ax+ b, то ее графиком является прямая; если квадратичная функция вида, то графиком является парабола.
- Нахождение некоторых точек на ней путем подстановки произвольных значений x и нахождение соответствующих значений y путем подстановки каждого значения в функцию.
Источник: unacademy.com
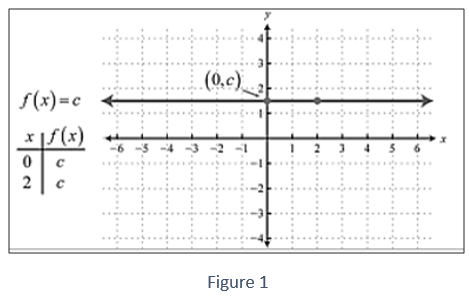
Постоянной функцией называется любая функция вида f(x)=c, где c может быть любым действительным числом. Постоянные функции линейны и имеют вид f(x)=0x+c. Из этой формы видно, что наклон равен 0, а перекресток y - (0,c). С получается при вычислении любого значения x, например x=2.
Графиком постоянной функции является горизонтальная линия. Доменная область состоит из всех действительных чисел R, а область действия — из единственного значения c.
Примеры решения задач
Определите, какие из следующих точек лежат на графике функции f(x) = 2x3 - 2? (a) (1, 1) (b) (1, 0) (c) (2, 6).
Решение:
Подставим каждую точку в заданную функцию и посмотрим, какая из них удовлетворяет функции.
(a) (1, 1) = (x, f(x))
1 = 2(1)3 - 2
1 = 2 - 2
1 = 0, нет
Таким образом, (1, 1) НЕ лежит на графике функции.
(b) (1, 0) = (x, f(x))
0 = 2(1)3 - 2
0 = 2 - 2
0 = 0, да
Таким образом, (1, 1) находится на графике функции.
(c) (2, 6) = (x, f(x))
6 = 2(2)3 - 2
6 = 16 - 2
6 = 14, нет.
Таким образом, (2, 6) НЕ лежит на графике функции.
Ответ: Только (b) лежит на заданной функции.
Вопрос: имеет ли график выше асимптоты? Сколько частей он имеет?
Решение: Данная функция f(x) = 2x3 - 2 является полиномиальной функцией и, следовательно, не имеет асимптот. Если асимптоты отсутствуют, то при построении графика функции мы получим только одну кривую (так как кривая нигде не ломается).
Ответ: Асимптоты отсутствуют, и кривая только одна.
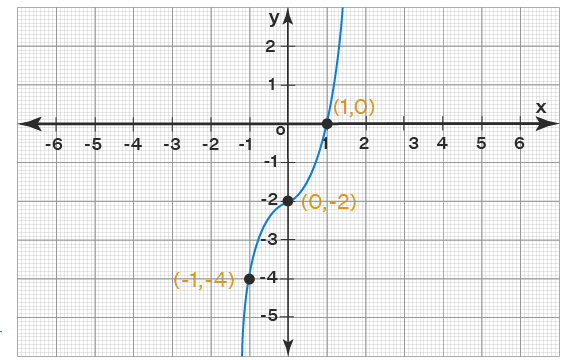
Постройте график функции из задания 1 с указанием точки (точек), в которой находится ее решение.
Решение: Ранее мы уже выяснили, что точка (1, 0) лежит на графике функции f(x) = 2x3 - 2. Для построения графиков функций необходимо большее количество точек. Для этого построим таблицу.
| x | y |
|---|---|
| -1 | 2(-1)3 - 2 = -4 |
| 0 | 2(0)3 - 2 = -2 |
Нанесем эти точки на график (1, 0) и построим его.
Источник: cuemath.com
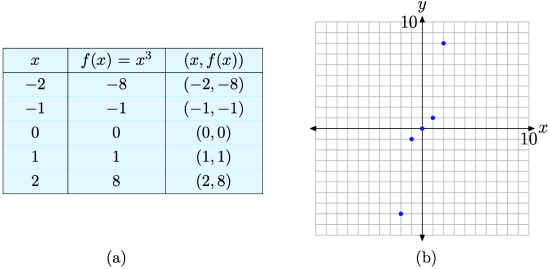
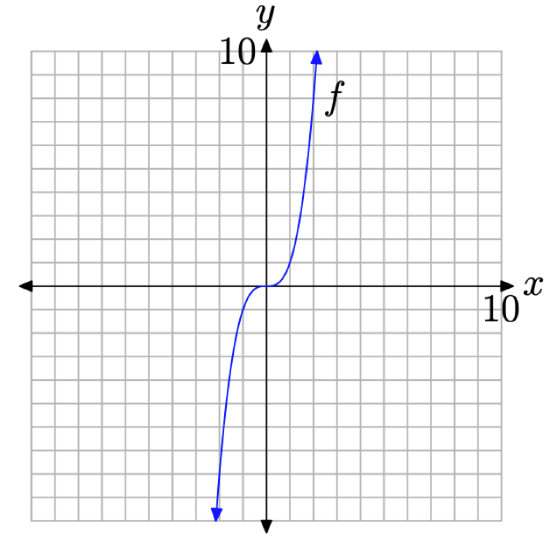
Набросать график функции, заданной уравнением f(x)=x3.
Решение:
Начнем со значений x -2,-1,0,1 и 2, затем воспользуемся уравнением f(x)=x3 для определения пар (x, f(x)) (например, f(-2)=(-2)3=-8). Они приведены в таблице.
Построение пар (x, f(x)), определяемых уравнением f(x)=x3.
Источник: math.libretexts.org
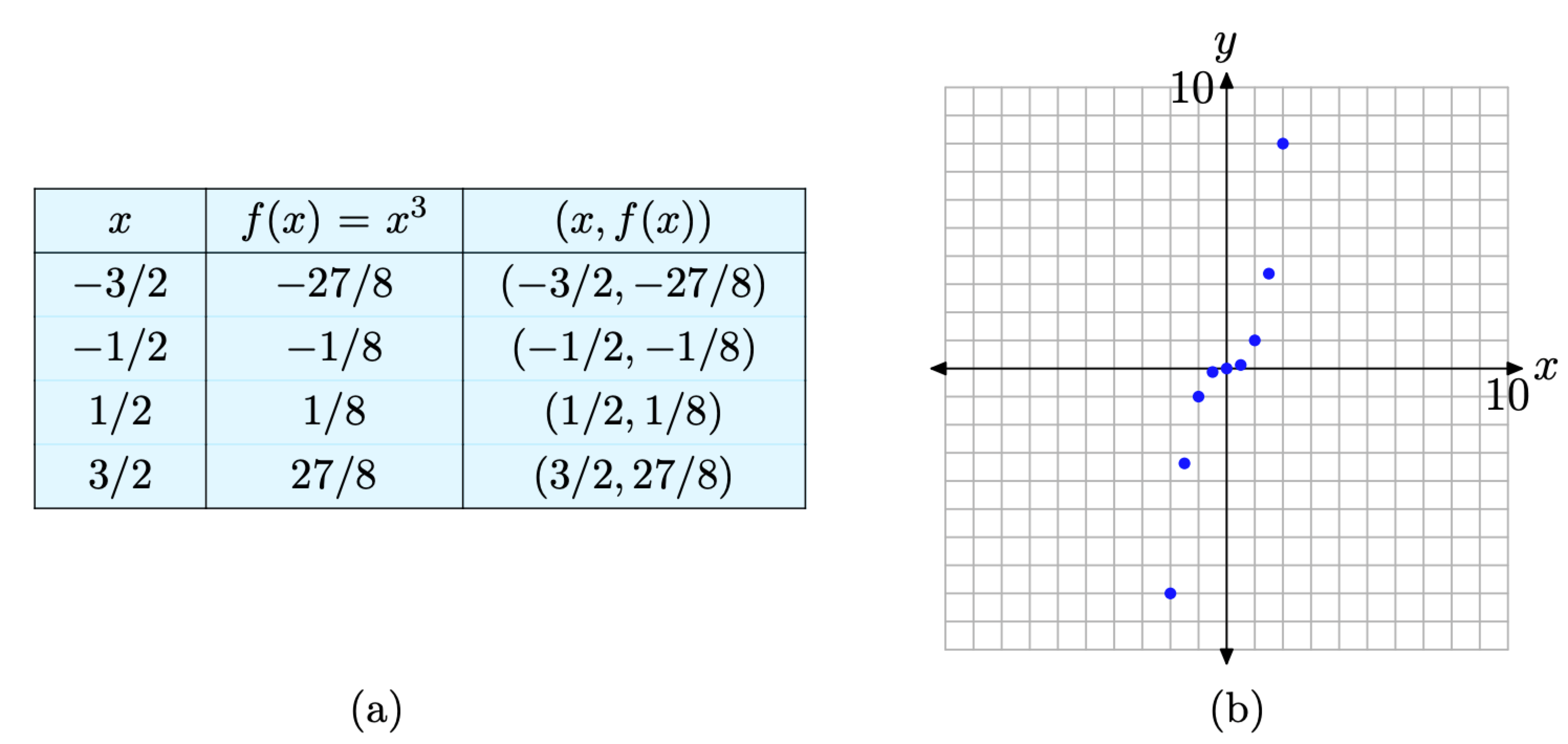
Затем строим график точек из таблицы в декартовой системе координат, как показано на рисунке. Добавим в нашу таблицу еще несколько пар и построим их график. Это показано ниже:
Построение дополнительных пар (x, f(x)), определяемых уравнением f(x)=x3.
Источник: math.libretexts.org
Окончательный график f(x)=x3:
Источник: math.libretexts.org
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так