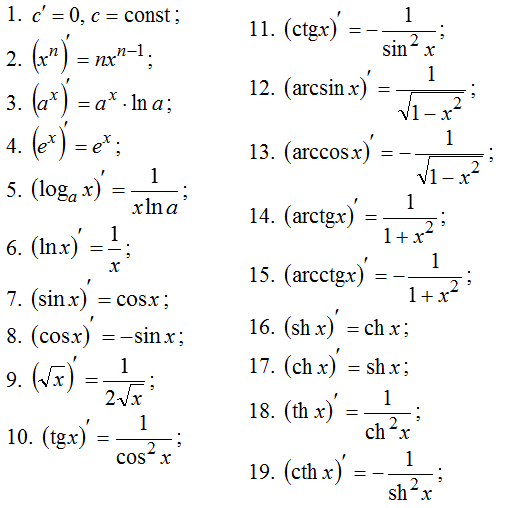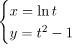Физический смысл производной функции

Физический смысл производной — понятие в математике

Производную функции рассчитывают, как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулевому значению при условии наличия такого предела. Функция, которая обладает конечной производной в какой-то точке, называется дифференцируемой в этой точке.

Физический смысл производной заключается в том, что скорость материальной точки в конкретное время \(t_{0}\) определяется, как производная закона движения \(s(t_{0})\) данной точки в определенный момент времени \(t_{0}: v(t_{0})=s^{,}(t_{0})\)

В чем заключается для производной функции первого и второго порядка

Производная первого порядка функции \(y=f(x)\) которая задана явно, определяется по таблице производных. Используют следующие данные:

Также в расчетах применяют правила дифференцирования или нахождения производных:

1. Константа может быть вынесена за знак производной: \((c*u(x))^{,}=c*(u(x))^{,}\)
2. Производная суммы или разности определяется таким образом: \((u\pm v)^{,}=u^{,}\pm v^{,}\)
3. Производная произведения: \((u* v)^{,}=u^{,}*v+ v^{,}*u\)
4. Производная частного двух функций: \((\frac{u}{v})^{,}=\frac{u^{,}v-uv^{,}}{v^{2}}\)

В том случае, когда функция y = y(x) задана параметрически в виде:

Где t является параметром, то первая производная данной функции будет определяться, согласно уравнению:

\(y^{,}(x)=\frac{y^{,}_{t}}{x^{,}_{t}}\)

В том случае, когда функция y = y(x) задана неявно, уравнение F(x;y(x)) = 0 или F(x;y(x)) = G(x;y(x)), для определения первой производной \(y=y^{,}(x)\) необходимо руководствоваться правилами. Вначале следует выполнить дифференцирование левой и правой части заданного равенства:

\((F(x;y(x)))^{,} = (0)^{,}\)

или

\((F(x;y(x)))^{,} = (G(x;y(x)))^{,}\)

Затем требуется найти производные от каждой из частей уравнения с помощью таблице производных и правил дифференцирования с учетом, что y является сложной функцией. Далее из полученного равенства выражают \((y)^{,}\)

Если рассмотреть дифференцируемую на (а;b) функцию y = f(x), то можно отметить, что ее производная \((y)^{,}\) также является функцией аргумента х. После повторного дифференцирования данной функции получится вторая производная функции y = f(x):

\(y^{,,}=(y^{,})^{,}\)

Таким образом, производная второго порядка представляет собой первую производную от производной первого порядка.

Как решать, примеры задач с пояснениями

Решение:

Скорость точки определяется производной пути по времени:

\(v(t)=s^{,}(t)=(4t^{2}+2t+1)^{,}=8t+2\)

Мгновенная скорость точки в момент времени \(t_{0}=2\) с равна:

\(v(t_{0})=v(2)=8*2+2=18\)

Ответ: мгновенная скорость движения материальной точки равна 18 м/с.

Решение:

С помощью физического смысла производной, можно определить закон изменения скорости материальной точки:

\(v(t)=s^{,}(t)=(3t^{2}-3t-5)^{,}=6t-3\)

Для того чтобы рассчитать момент времени \(t_{0}\) со скорость в 3 м/с, требуется записать и найти решение уравнения \(v(t_{0})=3\)

\(6t_{0}-3=3\)

\(t_{0}=1\)

Ответ: момент времени равен 1 с.

\(y=x^{2}-3x+\frac{x}{x+1}\)

Решение:

Искомая производная имеет следующий вид:

\(y^{,}=(x^{2}-3x+\frac{x}{x+1})^{,}\)

Производная суммы или разности функций определяется, как сумма или разность их производных:

\(y^{,}=(x^{2})^{,}-(3x)^{,}+(\frac{x}{x+1})^{,}\)

Производную первого слагаемого можно определить с помощью таблицы производных, как производную степенной функции \((x^{n})^{,}=nx^{n-1}\)

Таким образом:

\((x^{2})^{,}=2x^{2-1}=2x\)

Во втором слагаемом, исходя из свойства производных, требуется вынести константу 3 за знак производной:

\((3x)^{,}=3*(x) ^{,}\)

Далее необходимо найти производную по ранее записанной формуле производной степенной функции:

\((3x)^{,}=3*(x) ^{,}=3*(x^{1}) ^{,}=3*1*x^{1-1}=3*x^{0}=3*1=3\)

Производную третьего слагаемого можно определить в виде производной частного по формуле:

\((\frac{u}{v})^{,}=\frac{u^{,}v-uv^{,}}{v^{2}}\)

Если u=x, v=+1, то:

\((\frac{x}{x+1})^{,}=\frac{(x)^{,}*(x+1)-x*(x+1)^{,}}{(x+1)^{2}}=\frac{1*(x+1)-x*\left[(x)^{,} +(1)^{,}\right]}{(x+1)^{2}}=\frac{1}{(x-1)^{2}}\)

В случае заданной функции получается:

\(y^{,}=2x-3+\frac{1}{(x-1)^{2}}\)

Ответ: \(y^{,}=2x-3+\frac{1}{(x-1)^{2}}\)

 

Решение:

Исходя из формулы, требуется определить производные для каждой функции относительно параметра t:

\(x^{,}_{t}=(ln t)^{,}_{t}=\frac{1}{t}\)

\(y^{,}_{t}=(t^{2}-1)^{,}_{t}=(t^{2})^{,}_{t}-(1)^{,}_{t}=2t-0=2t\)

В таком случае, искомая производная равна:

\(y^{,}(x)=\frac{y^{,}_{t}}{x^{,}_{t}}=\frac{2t}{\frac{1}{t}}=2t*t=2t^{2}\)

Ответ: \(y^{,}(x)=2t^{2}\)

\(y=x^{3}-4x+13\)

Решение:

Определить вторую производную можно, если вначале найти производную второго порядка:

\(y^{,}=(x^{3}-4x+13) ^{,}\)

Исходя из свойства линейности, получим:

\(y^{,}=(x^{3})^{,}-4*(x) ^{,}+(13) ^{,}=3x^{2}-4*1+0=3x^{2}-4\)

В таком случае, искомая вторая производная будет равна:

\((3x^{2}-4)^{,}=3*(x^{2})^{,}-(4)^{,}=3*2x-0=6x\)

Ответ: \(y^{,}=6x\)

\(x^{2}+xy-\cos y=x\)

Решение:

Необходимо дифференцировать две части заданного равнения:

\((x^{2}+xy-\cos y)^{,}=x^{,}\)

Исходя из правил дифференцирования и таблице производных, получим следующее уравнение:

\((x^{2})^{,}+(xy)^{,}-(\cos y)^{,}=1\)

\(2x+(x)^{,}*y+x*(y) ^{,}-(-\sin y)(y)^{,}=1\)

\(2x+1*y+x*(y)^{,}+\sin y*(y)^{,}=1\)

\(2x+y+x*y^{,}+\sin y*(y)^{,}=1\)

Согласно полученному выражению, можно определить \(y^{,}\)

\((x+\sin y)*y^{,}=1-2x-y\Rightarrow y^{,}=\frac{1-2x-y}{x+\sin y}\)

Ответ: \(y^{,}=\frac{1-2x-y}{x+\sin y}\)