Координаты фокуса параболы: как найти, формула
Формулировка параболы в алгебре и геометрии
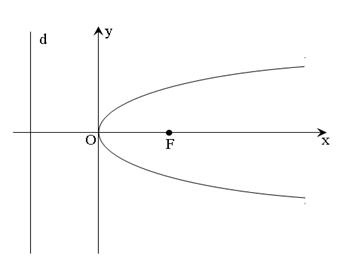
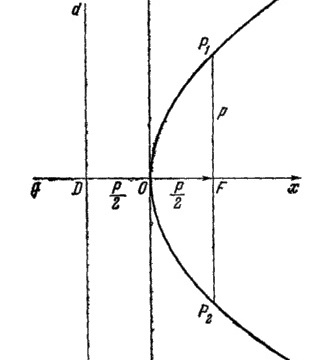
Парабола — совокупность точек на плоскости, расположенных на одинаковом удалении от фокуса F и директрисы d, в которую точка F не входит.
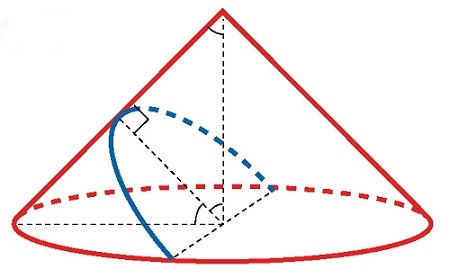
Парабола является коническим сечением, или коникой. Это значит, что она возникает при пересечении плоскости с поверхностью кругового конуса. Плоскость сечения при этом параллельна одной из касательных плоскостей конуса.
Точка пересечения параболы с ее осью называется вершиной. Она считается началом системы координат, канонической для данной кривой.
Что такое фокус параболы, определение
Расстояние от точки фокуса до любой точки параболы равняется расстоянию от этой точки к директрисе.
Если в фокус поместить источник света, все исходящие из него световые лучи после отражения от нее пойдут по прямым, параллельным оси симметрии. И наоборот, все световые лучи, идущие параллельно оси, после отражения от «стенок» кривой соберутся в одной точке. Это оптическое свойство широко применяется в конструкциях прожекторов, фар, фонарей, телескопов-рефлекторов.
Как найти фокус параболы
Уравнение расчета
Каноническое уравнение:
\(y^2\;=\;2px\)
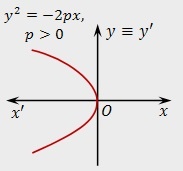
Если расположить параболу слева от оси ординат, уравнение примет вид:
\(y^2\;=\;-\;2px\)
Параметр p — расстояние от фокуса до директрисы, которая определяется уравнением:
\(х\;=\;-\frac p2\)
Чтобы узнать расстояние r от любой точки параболы до фокуса, равное ее расстоянию до директрисы, нужно воспользоваться формулой:
\(r\;=\;\frac p2\;+\;x\)
В полярной системе координат с центром в фокусе и направлением вдоль оси фокальный параметр можно найти по формуле:
\(p\;=\;\rho\;\times\;(1\;+\;\cos\left(\vartheta\right))\)
Чему равны координаты фокуса
Фокус будет иметь координаты \((\frac p2;\;0)\).
Абсцисса фокуса параболы
Также фокус и параметр p можно искать через так называемую фокальную хорду \(Р_1Р_2\).
Эта прямая, проходящая через фокус и параллельная директрисе, пересекает параболу в двух точках. Половина длины фокальной хорды будет равна параметру p, являясь абсолютной величиной ординаты любой из точек \(Р_1, Р_2\).
Абсцисса каждой из этих точек будет равна абсциссе фокуса \(\frac p2\).
Для ординаты y каждой из точек \(Р_1, Р_2\):
\(y^{2\;}=\;2p\;\times\;\frac p2\;=\;p^2\).
Примеры расчета фокусного расстояния в задачах
Пример 1
Определить координаты фокуса параболы \(y^{2\;}=\;4х\).
Решение
Находим параметр p:
4 = 2p
p = 2
Координаты (1; 0).
Пример 2
Определить координаты фокуса параболы \(y^{2\;}=\;6х\).
Решение
Находим параметр p:
6 = 2p
p = 3
Координаты (1,5; 0).
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так