Что можно вычислить по формуле Герона

Формула Герона

Формула Герона носит такое название в честь греческого математика и инженера Герона Александрийского. Он жил в I веке нашей эры. Герон занимался механикой, оптикой, геометрией и гидростатикой. Учёный интересовался треугольниками с целочисленными сторонами и целочисленными площадями. Такие фигуры получили название Героновых треугольников.

Формулировка теоремы Герона

Формула Герона – это арифметическая формула для вычисления площади треугольника по длинам его сторон. В таком случае площадь равна корню из произведения разностей полупериметра и каждой из его сторон.

Формула и доказательство

Формула Герона выглядит следующим образом:

\(S\;=\;\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)

где S – это площадь треугольника; a, b, c – это стороны треугольника; p – это полупериметр треугольника.

Чтобы вычислять полупериметр, нужно пользоваться формулой:

\(p\;=\;\frac{a+b+c}2\)

Приведем доказательство.

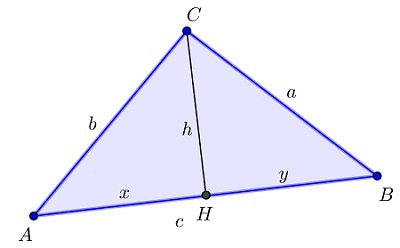
Для этого рассмотрим треугольник ABC.

\(\left|AB\right|=c,\;\left|BC\right|=a,\;\left|AC\right|=b\)

CH – высота треугольника.

\(\left|CH\right|=h,\;\left|AH\right|=x,\;\left|BH\right|=y\)

Тогда \(c=x+y\).

По теореме Пифагора из треугольников ACH и BCH получаем:

\(h^2=b^2-x^2=a^2-y^2\)

Из этого:

\(y^2-x^2=a^2-b^2\)

\((y-x)(y+x)=a^2-b^2\)

\(x+y=c\)

Соответственно:

\((y-x)c=a^2-b^2\) и \(y-x=\frac1c (a^2-b^2)\)

Если сложить последнее равенство с \(y+x=c\), то получается

\(y\;=\;\frac{c^2+a^2-b^2}{2c}\)

Найдем высоту треугольника.

\(h^2\;=\;a^2-y^2=\left(a-y\right)\left(a+y\right)=\left(a-\frac{c^2+a^2-b^2}{2c}\right)\left(a+\frac{c^2+a^2-b^2}{2c}\right)=\frac{2ac-c^2-a^2+b^2}{2c}\times\frac{2ac+c^2+a^2-b^2}{2c}=\frac{b^2-\left(a-c\right)^2}{2c}\times\frac{\left(a+c\right)^2-b^2}{2c}=\frac{\left(b-a+c\right)\times\left(b+a-c\right)}{2c}\times\frac{\left(a+c-b\right)\times\left(a+c+b\right)}{2c}\)

Так как \(p=\frac12\left(a+b+c\right)\), то \( b+c=2p-a\),\( a+b=2p-c\), \(a+c=2p-b\), \(a+b+c=2p\).

С помощью этих равенств найдем высоту.

\(h^2=\frac{\left(2p-2a\right)\left(2p-2c\right)\left(2p-2b\right)2p}{4c^2}=\frac{4p\left(p-a\right)\left(p-c\right)\left(p-b\right)}{c^2}\)

А так как \(S=\frac12ch\), то теорема доказана.

Для каких треугольников действует теорема

Применение формулы Герона допустимо для треугольников, у которых известны длины всех их сторон.

Примеры решения задач

Задача 1

Рассчитать площадь треугольника, если a=6, b=8, c=6.

Решение

\(p=\frac{6+8+6}2=10\)

Тогда площадь треугольника равна:

\(S=10\sqrt{\left(10-6\right)\left(10-8\right)\left(10-6\right)}=320\)

Ответ: 320 см².

Задача 2

Вычислить площадь параллелограмма, если одна из его сторон равна 51, а диагонали равны 40 и 74.

Решение

Диагонали AC и BD  пересекаются в точке O.

Если  AD = 51,  AC = 40  и  BD = 74,  то  AO = 20,  OD = 37.

По формуле Герона:

\(S_{ABCD} = 4S_{AOD} = \sqrt{54\left(54-51\right)\left(54-37\right)\left(54-20\right)}=1224\)

Ответ: 1224 см². 

Задача 3

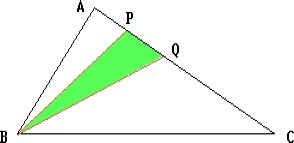
В треугольнике ABC три стороны:  AB = 26,  BC = 30  и  AC = 28. Найти часть площади этого треугольника, заключённую между высотой и биссектрисой, проведёнными из вершины B.

Решение

BP и BQ – высота и биссектриса треугольника.

По формуле Герона:

\(S=\sqrt{42\left(42-30\right)\left(42-28\right)\left(42-26\right)}=336\)

\(S = ½ AC·BP\)

Поэтому  \(BP =\frac{2S}{AC}=\frac{2\times336}{28}=24\).

По свойству биссектрисы треугольника:

\(\frac{AQ}{QC}=\frac{AB}{BC}=\frac{26}{30}=\frac{13}{15}\)

Соответственно \(AQ=\frac{13}{28}AC = 13\).

По теореме Пифагора из треугольника APB получаем:

\(AP=\sqrt{AP^2-BP^2}=\sqrt{26^2-24^2}=\sqrt{2\times50}=10\)

Следовательно,  \(PQ = AQ – AP = 13 – 10 = 3\)

\(S_{BPQ} = ½ PQ·BP = \frac{3\times24}2=36\)

Ответ: 36 см².