Применение формулы Грина для вычисления криволинейных интегралов
Формула Грина — что из себя представляет
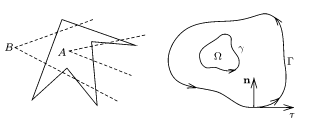
Перед рассмотрением темы важно подчеркнуть, что область в \(\boldsymbol{R}^{2} \) представляет собой открытое связное множество. К замыканию области приводит присоединение границ. Согласно теореме Жордана, любая простая, исключая точки самопересечения, замкнутая кривая образует в плоскости пару областей, ограниченную и неограниченную. Данная кривая является общей границей полученных областей.
Область \(\Omega \subset \boldsymbol{R}^{2} \)представляет собой односвязную область в том случае, когда для любого простого контура \(\gamma \subset \Omega\) ограничиваемая этим контуром область \(\Omega_{1} \subset \Omega\). Например, область, изображенная на рисунке, является односвязной.
Предположим, что простой контур \(\Gamma\) имеет положительную ориентацию тогда, когда при обходе контура ограничиваемая им область остается с левой стороны. Контур, ориентированный в противоположном направлении, можно обозначить, как \(\Gamma^{-}\).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
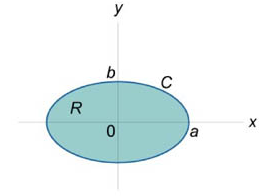
Допустим, что плоскость Oxy содержит область R, ограниченную замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некой области, в которой находится R, задана непрерывная векторная функция:
\(\mathbf{F} = P\left( {x,y} \right)\mathbf{i} + Q\left( {x,y} \right)\mathbf{j}\).
Рассматриваемая функция обладает непрерывными частными производными первого порядка:
\(\large\frac{{\partial P}}{{\partial y}}\normalsize\);
\(\large\frac{{\partial Q}}{{\partial x}}\normalsize\).
В таком случае, справедлива формула Грина:
\({\iint\limits_R {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)dxdy} } = {\oint\limits_C {Pdx + Qdy} ,}\)
где символ \(\oint\limits_C {}\) говорит о том, что кривая (контур) \(C\) является замкнутой, и обход в процессе интегрирования вдоль рассматриваемой кривой выполняется против часовой стрелки.
Если \(Q = x, P = -y\), то формула Грина принимает вид:
\(S = \iint\limits_R {dxdy} = \frac{1}{2}\oint\limits_C {xdy - ydx}\),
где S — обозначает площадь области R, которая ограничена контуром C.
Формулу Грина допускается записывать в векторной форме. Перед этим следует ввести определение ротора векторного поля.
Предположим, что векторное поле можно описать с помощью функции:
\(\mathbf{F} = P\left( {x,y,z} \right)\mathbf{i} + Q\left( {x,y,z} \right)\mathbf{j} + R\left( {x,y,z} \right)\mathbf{k}\)
Ротор или вихрь векторного поля \(\mathbf{F}\) — это вектор, обозначенный как \(\text{rot}\,\mathbf{F}\) или \(\nabla \times \mathbf{F}\), и равный: \({\text{rot}\,\mathbf{F} = \nabla \times \mathbf{F} } = {\left| {\begin{array}{*{20}{c}} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ {\frac{\partial }{{\partial x}}}&{\frac{\partial }{{\partial y}}}&{\frac{\partial }{{\partial z}}}\\ P&Q&R \end{array}} \right| } = {{\left( {\frac{{\partial R}}{{\partial y}} - \frac{{\partial Q}}{{\partial z}}} \right)\mathbf{i} } + {\left( {\frac{{\partial P}}{{\partial z}} - \frac{{\partial R}}{{\partial x}}} \right)\mathbf{j} } + {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)\mathbf{k}.}}\)
Формула Грина в векторной форме имеет следующий вид: \({\iint\limits_R {\left( \text{rot}\,\mathbf{F} \right) \cdot \mathbf{k}\,dxdy} } = {\oint\limits_C {\mathbf{F} \cdot d\mathbf{r}} .}\)
При рассмотрении формулы Грина можно заметить, что она является следствием теоремы Стокса при переходе от трехмерного случая к случаю двух координат.
Вывод, доказательство для чайников
Определение
При наличии функций \(P(x, y)\) и \(Q(x, y)\), непрерывно дифференцируемых в односвязной области \(\Omega \subset \boldsymbol{R}^{2}\), и простого кусочно гладкого контура \(\Gamma \subset \Omega\), ограничивающего область \( G \subset \Omega\), справедлива формула Грина: \(\int\limits_{\partial G} P\ dx + Q\ dy = \iint\limits_{G} \left[\frac{\partial Q(x, y)}{\partial x}-\frac{\partial P(x, y)}{\partial y}\right]\ dx\ dy\), где \(\partial G\) — является положительно ориентированной границей области \(G\).
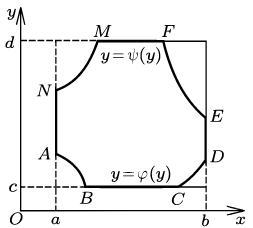
В процессе доказательства теоремы следует в первую очередь подтвердить корректность формулы, записанной в максимально простой форме, при элементарной относительно обеих координатных осей области \(G\). То есть имеются такие кусочно непрерывно дифференцируемые и непрерывные функции:
- \(\varphi(x)\);
- \(\psi(x)\);
- \(x \in [a, b]\);
- \(\alpha(y)\);
- \(\beta(y)\);
- \(y \in [c, d]\).
\(\overline{G} = \{(x, y): a \leq x \leq b,\ \varphi(x) \leq y \leq \psi(x)\} = \{(x, y): c \leq y \leq d,\ \alpha(x) \leq x \leq \beta(x)\}.\)
В качестве примеров подобных областей можно привести внутренние пространства в круге, эллипсе, треугольнике.
Путем применения формулы сведения двойного интеграла к повторному можно записать следующее выражение:
\(\iint\limits_{G} \frac{\partial P}{\partial y} (x, y)\ dx\ dy =-\int\limits_{a}^{b} dx \int\limits_{\varphi(x)}^{\psi(x)} \frac{\partial P}{\partial y} (x, y)\ dx\ dy =\\= \int\limits_{a}^{b} P(x, \varphi(x))dx-\int\limits_{a}^{b} P(x, \psi(x))dx =\\= \int\limits_{ABCD} P\ dx + \int\limits_{DE} P\ dx + \int\limits_{EFMN} P\ dx + \int\limits_{NA} P\ dx = \int\limits_{\partial G} P\ dx.\)
При выводе уравнения применена формула для криволинейного интеграла \(\int\limits_{\Gamma} P\ dx\) по кривой \Gamma, которая представляет собой график функции. Добавленные интегралы по вертикальным отрезкам DE и NA имеют нулевые значения. Это объясняется \(x = \operatorname{const}\).
Аналогичным методом можно доказать равенство:
\(\iint\limits_{G} \frac{\partial Q(x, y)}{\partial x}\ dx\ dy = \int\limits_{\partial G} Q(x, y)\ dy.\)
Путем сложения записанных формул получим формулу Грина.
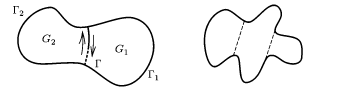
В другом случае предположим, что область G ограничена кусочно гладкой замкнутой кривой \(\partial G\). Представим, что при делении данной области с помощью кусочно гладкой простой кривой \(\Gamma\) (перегородкой) получаем две области простейшего вида, которые были рассмотрены на первом рисунке. В таком случае:
\(\partial G_{1} = \Gamma \cup \Gamma_{1},\ \partial G_{2} = \Gamma^{-} \cup \Gamma_{2} \)
Применив формулу Грина для каждой из областей \(G_{1} и G_{2}\), получим:
\(\iint\limits_{G_{1}} \left[\frac{\partial Q(x, y)}{\partial x}-\frac{\partial P(x, y)}{\partial y}\right]\ dx\ dy = \int\limits_{\partial G} P\ dx + Q\ dy = \int\limits_{\Gamma_{1}} P\ dx + Q\ dy + \int\limits_{\Gamma} P\ dx + Q\ dy,\)
\(\iint\limits_{G_{1}} \left[\frac{\partial Q(x, y)}{\partial x}-\frac{\partial P(x, y)}{\partial y}\right]\ dx\ dy = \int\limits_{\Gamma_{2}} P\ dx + Q\ dy + \int\limits_{\Gamma^{-}} P\ dx + Q\ dy.\)
Если сложить данные равенства с учетом взаимного исключения криволинейных интегралов по противоположно ориентированным кривым \(\Gamma и \Gamma^{-}\), то в результате будет доказана справедливость формулы Грина для области \(G = G_{1} \cup G_{2}\).
С помощью математической индукции достаточно просто привести формулу Грина к общему виду на односвязную область, которая при помощи n-1 непересекающихся гладких перегородок разбивается на области \(G_{1}, \ldots, G_{n}\) простейшего вида.
К примеру, формула Грина обобщается на области со многими углами, которые ограничены простыми замкнутыми ломаными. В общем случае можно доказать формулу Грина, аппроксимируя область с кусочно гладкой границей многоугольной областью.
В качестве практического примера можно решить задачу на проверку формулы Грина для области интегрирования R, которая является кругом с радиусом 2 и имеет центр, совпадающий с началом координат, и векторного поля \( \mathbf{F }\left( {P,Q} \right) = \left( {{x^2}{y^2},x{y^2}} \right)\).
В первую очередь следует определить криволинейный интеграл для рассматриваемого векторного поля. Контур интегрирования в данном случае представляет собой соответствующую окружность, то есть область R.
\({I_1} = \oint\limits_C {Pdx + Qdy} = \oint\limits_C {{x^2}{y^2}dx + x{y^2}dy}\)
С помощью параметрических уравнений окружности запишем:
\({x = 2\cos t,}\;\; {y = 2\sin t,}\;\; {0 \le t \le 2\pi ,}\)
Таким образом:
\({{I_1} = \int\limits_0^{2\pi } {\left[ {{{\left( {2\cos t} \right)}^2} \cdot {{\left( {2\sin t} \right)}^2} \cdot \frac{{d\left( {2\cos t} \right)}}{{dt}} + 2\cos t \cdot {{\left( {2\sin t} \right)}^2} \cdot \frac{{d\left( {2\sin t} \right)}}{{dt}}} \right]dt} } = {\int\limits_0^{2\pi } {\left[ {16\,{{\cos }^2}t\,{{\sin }^2}t \cdot \left( { - 2\sin t} \right) + 8\cos t\,{{\sin }^2}t \cdot 2\cos t} \right]dt} } = {\int\limits_0^{2\pi } {\left[ {16\,{{\cos }^2}t\,{{\sin }^2}t\left( {1 - 2\sin t} \right)} \right]dt} } = {4\int\limits_0^{2\pi } {{{\left( {\sin 2t} \right)}^2}\left( {1 - \sin 2t} \right)dt} } = {4\int\limits_0^{2\pi } {\frac{{1 - \cos 4t}}{2} \cdot \left( {1 - \sin 2t} \right)dt} } = {2\int\limits_0^{2\pi } {\left( {1 - \cos 4t - \sin 2t + \sin 2t\cos 4t} \right)dt} } = {2\int\limits_0^{2\pi } {\left[ {1 - \cos 4t - \sin 2t + \frac{1}{2}\left( {\sin 6t + \sin \left( { - 2t} \right)} \right)} \right]dt} .}\)
В данной ситуации целесообразно использовать тригонометрическую формулу:
\({\sin \alpha \cos \beta } = {\frac{1}{2}\left[ {\sin \left( {\alpha + \beta } \right) + \sin \left( {\alpha - \beta } \right)} \right].}\)
В результате можно вычислить криволинейный интеграл \({I_1}\):
\({{I_1} = \int\limits_0^{2\pi } {\left( {2 - 2\cos 4t - 3\sin 2t + \sin 6t} \right)dt} } = {\left. {\left( {2t - \frac{{\sin 4t}}{2} + \frac{{3\cos 2t}}{2} - \frac{{\cos 6t}}{6}} \right)} \right|_0^{2\pi } } = {\left( {4\pi + \frac{3}{2} - \frac{1}{6}} \right) - \left( {\frac{3}{2} - \frac{1}{6}} \right) } = {4\pi .}\)
Далее необходимо определить двойной интеграл:
\({{I_2} = \iint\limits_R {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)dxdy} } = {\iint\limits_R {\left( {\frac{{\partial \left( {x{y^2}} \right)}}{{\partial x}} - \frac{{\partial \left( {{x^2}{y^2}} \right)}}{{\partial y}}} \right)dxdy} } = {\iint\limits_R {\left( {{y^2} - 2y{x^2}} \right)dxdy} .}\)
В полярных координатах интеграл обладает следующим значением:
\({{I_2} = \iint\limits_R {\left( {{y^2} - 2y{x^2}} \right)dxdy} } = {\int\limits_0^{2\pi } {\int\limits_0^2 {\left[ {{{\left( {r\sin \theta } \right)}^2} - 2r\sin \theta {{\left( {r\cos \theta } \right)}^2}} \right]rdrd\theta } } } = {\int\limits_0^{2\pi } {\left[ {\int\limits_0^2 {\left( {{r^2}{{\sin }^2}\theta - 2{r^3}\sin \theta \,{{\cos }^2}\theta } \right)rdr} } \right]d\theta } } = {\int\limits_0^{2\pi } {\left[ {\int\limits_0^2 {\left( {{r^3}{{\sin }^2}\theta - 2{r^4}\sin \theta \,{{\cos }^2}\theta } \right)dr} } \right]d\theta } } = {\int\limits_0^{2\pi } {\left[ {\left. {\left( {\frac{{{r^4}}}{4}{{\sin }^2}\theta - \frac{{2{r^5}}}{5}\sin \theta \,{{\cos }^2}\theta } \right)} \right|_{r = 0}^2} \right]d\theta } } = {\int\limits_0^{2\pi } {\left( {4{{\sin }^2}\theta - \frac{{64}}{5}\sin \theta \,{{\cos }^2}\theta } \right)d\theta } } = {4\int\limits_0^{2\pi } {{{\sin }^2}\theta d\theta } - \frac{{64}}{5}\int\limits_0^{2\pi } {\sin \theta \,{{\cos }^2}\theta d\theta } } = {4\int\limits_0^{2\pi } {\frac{{1 - \cos 2\theta }}{2}d\theta } } + {\frac{{64}}{5}\int\limits_0^{2\pi } {{{\cos }^2}\theta \,d\left( {\cos \theta } \right)} } = {2\left[ {\left. {\left( {\theta - \frac{{\sin 2\theta }}{2}} \right)} \right|_0^{2\pi }} \right] } + {\frac{{64}}{5}\left[ {\left. {\left( {\frac{{{{\cos }^3}\theta }}{3}} \right)} \right|_0^{2\pi }} \right] } = {4\pi .}\)
Таким образом, проверка выполнена:
{I_1} = {I_2}.
Вычисление площади области по формуле Грина
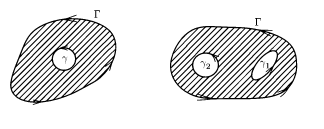
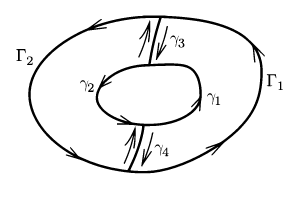
Допустимо обобщение формулы Грина в том случае, когда область является многосвязной (n-связной), ограничена внешним контуром \Gamma и внутренними контурами \(\gamma_{1}\), \(\ldots, \gamma_{n-1}\), которые не пересекаются. Каждый контур является кусочно гладким. На рисунке представлены ограниченные двусвязная и трехсвязная области:
Внешний контур следует направить таким образом, чтобы при его обходе область оставалась с левой стороны. Можно ввести для ориентированного контура обозначение \(\Gamma\). Внутренние контуры следует ориентировать так, чтобы при их обходе область G располагалась с правой стороны. В результате получим равенство:
\(\partial G = \left(\bigcup_{i=1}^{n} \gamma_{i}^{-}\right) \bigcup \Gamma\)
Предположим, что непрерывно дифференцируемое поле \((P(x, y), Q(x, y))\) задано в двусвязной области \(G\), которая ограничена кусочно гладкими простыми контурами:
- внешним \(\Gamma\);
- внутренним \(\gamma\).
С помощью гладких перегородок \(\gamma_{3}\) и \(\gamma_{4}\) можно выделить в двусвязной области \(G\) пару:
- \(G_{1}\);
- \(G_{2}\).
\(\Gamma = \Gamma_{1} \cup \Gamma_{2},\ \gamma = \gamma_{1} \cup \gamma_{2}\)
Если применить формулу Грина для областей \(G_{1} и G_{2}\), то получим следующее равенство:
\(\iint\limits_{G_{1}} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) dx\ dy = \int\limits_{\partial G_{1}} P\ dx + Q\ dy = \left(\int\limits_{\Gamma_{1}} + \int\limits_{\gamma_{3}} + \int\limits_{\gamma_{1}^{-}} + \int\limits_{\gamma_{4}}\right) (P\ dx + Q\ dy)\),
\(\iint\limits_{G_{2}} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) dx\ dy = \int\limits_{\partial G_{1}} P\ dx + Q\ dy = \left(\int\limits_{\Gamma_{2}} + \int\limits_{\gamma_{4}^{-}} + \int\limits_{\gamma_{2}^{-}} + \int\limits_{\gamma_{3}^{-}}\right) (P\ dx + Q\ dy)\)
В данном случае справа находится сокращенное обозначение для суммы четырех криволинейных интегралов по соответствующим кривым. Суммируя записанные выражения с учетом взаимного исключения криволинейных интегралов по противоположно ориентированным кривым, получим:
\(\iint\limits_{G} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) dx\ dy = \int\limits_{\Gamma} P\ dx + Q\ dy + \int\limits_{\gamma^{-}} P\ dx + Q\ dy = \int\limits_{\partial G} P\ dx + Q\ dy.\)
Формально формула Грина для двусвязной области обладает таким же видом, как и в случае односвязной области при условии, что \(\displaystyle\int\limits_{\partial G} P\ dx + Q\ dy\) является суммой криволинейных интегралов по \(\Gamma и \gamma^{-}.\)
С помощью индукции формулу Грина можно обобщить и на n-связную область:
\(\iint\limits_{G} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) dx\ dy = \int\limits_{\partial G} P\ dx + Q\ dy = \int\limits_{\Gamma} P\ dx + Q\ dy + \sum_{i=1}^{\substack{n-1}} \int\limits_{\gamma_{i}^{-}} P\ dx + Q\ dy.\)
При вводе обозначений \(\eqref{ref1} Q = x, P = -y\) в формулу Грина можно записать уравнение для определения площади, которая ограничена гладким контуром:
\(m(G) = \frac{1}{2} \int\limits_{\partial G} x\ dy-y\ dx\).
В некоторых практических случаях при использовании представленной формулы целесообразно учитывать, что:
\(x\ dy-y\ dx = (x^{2} + y^{2})d\left(\operatorname{arctg} \frac{y}{x}\right)\)
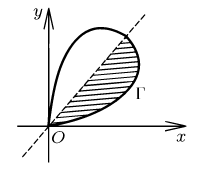
Расчет площади с помощью формулы Грина удобно рассмотреть на примере задачи. Допустим, что имеется некая площадь, ограниченная кривой, которую необходимо определить:
\(x = \frac{3at}{1 + t^{3}},\quad y = \frac{3at^{2}}{1 + t^{3}},\quad 0 \leq t \leq +\infty.\)
Рассматриваемая кривая (декартов лист) симметрична по отношению к прямой \(y = x\). В связи с этим, в процессе решения задачи допустимо ограничиться вычислением площади ½ листа, для которой \(0 \leq t \leq 1\). В таком случае:
\(x\ dy-y\ dx = (x^{2} + y^{2})d\left(\operatorname{arctg} \frac{y}{x}\right) = \frac{9a^{2}t^{2}(1 + t^{2})}{(1 + t^{3})^{2}}d(\operatorname{arctg} t) = \frac{9a^{2}t^{2}}{(1 + t^{3})^{2}}dt = -3a^{2}\ d\left(\frac{1}{1 + t^{3}}\right)\).
Исходя из формулы Грина, площадь половины листа Декарта составляет:
\(m(G) = \frac{1}{2} \int\limits_{\Gamma} x\ dy-y\ dx = -\frac{3a^{2}}{2} \int\limits_{0}^{1} d\left(\frac{1}{1 + t^{3}}\right) = \frac{3a^{2}}{4}\),
Искомая площадь равна:
\(\displaystyle\frac{3a^{2}}{2}\).
Усложняя условия задачи, предположим, что требуется определить площадь области R, которая ограничена астроидой:
\(x = a\,{\cos ^3}t, y = a\,{\sin ^3}t, 0 \le t \le 2\pi\).
В таком случае можно рассчитать площадь рассматриваемой области, применяя криволинейный интеграл по формуле:
\({\large\frac{1}{2}\normalsize}\oint\limits_C {xdy - ydx}\) .
В параметрическом виде уравнение будет записано таким образом:
\(S = \frac{1}{2}\int\limits_\alpha ^\beta {\left( {x\left( t \right)\frac{{dy}}{{dt}} - y\left( t \right)\frac{{dx}}{{dt}}} \right)dt} \).
Путем подстановки в формулу астроиды, получим:
\({S = \frac{1}{2}\int\limits_\alpha ^\beta {\left[ {a\,{{\cos }^3}t \cdot \frac{{d\left( {a\,{{\sin }^3}t} \right)}}{{dt}} - a\,{{\sin }^3}t \cdot \frac{{d\left( {a\,{{\cos }^3}t} \right)}}{{dt}}} \right]dt} } = {\frac{1}{2}\int\limits_0^{2\pi } {\left[ {a\,{{\cos }^3}t \cdot 3a\,{{\sin }^2}t\cos t - a\,{{\sin }^3}t \cdot 3a\,{{\cos }^2}t\left( { - \sin t} \right)} \right]dt} } = {\frac{{3{a^2}}}{2}\int\limits_0^{2\pi } {\left[ {{{\cos }^4}t\,{{\sin }^2}t + {{\sin }^4}t\,{{\cos }^2}t} \right]dt} } = {\frac{{3{a^2}}}{8}\int\limits_0^{2\pi } {\left[ {4\,{\sin^2}t\,{{\cos }^2}t\left( {{{\cos }^2}t + {{\sin }^2}t} \right)} \right]dt} } = {\frac{{3{a^2}}}{8}\int\limits_0^{2\pi } {{{\left( {\sin 2t} \right)}^2}dt} } = {\frac{{3{a^2}}}{8}\int\limits_0^{2\pi } {\frac{{1 - \cos 4t}}{2}dt} } = {\frac{{3{a^2}}}{{16}}\int\limits_0^{2\pi } {\left( {1 - \cos 4t} \right)dt} } = {\frac{{3{a^2}}}{{16}}\left[ {\left. {\left( {t - \frac{{\sin 4t}}{4}} \right)} \right|_0^{2\pi }} \right] } = {\frac{{3{a^2}}}{{16}} \cdot 2\pi } = {\frac{{3{a^2}\pi }}{8}.}\)
Применение формулы Грина для вычисления криволинейных интегралов
Допустим, что область \(G \subset \boldsymbol{R}^{2}\) имеет непрерывное векторное поле \((P(x, y), Q(x, y))\). К примеру, данным полем является силовое поле. Можно задать в области \(G\) пару произвольных точек:
- \(A\)\((x_{0}, y_{0})\);
- \(B(x, y)\).
Далее следует соединить эти две точки с помощью кусочно гладкой кривой \(\Gamma_{AB}\), принадлежащей области \(G\), и определить интеграл:
\(\displaystyle\int\limits_{\Gamma_{AB}} P\ dx + Q\ dy\).
Записанный интеграл допустимо интерпретировать в виде работы силы в процессе движения точки по кривой \(\Gamma_{AB}\). Таким образом, \(\displaystyle\int\limits_{\Gamma_{AB}} P\ dx + Q\ dy\) определяется точками \(A\) и \(B\), а также путем, соединяющим точки \(А\) и \(В\). Требуется установить, каковы условия независимости величины рассматриваемого интеграла (работы силы) от пути интегрирования.
Теорема
Следующие три условия являются эквивалентными:
- для любой замкнутой ломаной \(L \subset G: \int\limits_{L} P\ dx + Q\ dy = 0\);
- \(\displaystyle\int\limits_{L_{AB}} P\ dx + Q\ dy\) не зависит от ломаной \(L_{AB} \subset G\), которая соединяет точки \(A\) и \(B\);
- поле \((P(x, y), Q(x, y))\) является потенциальным, то есть имеется такая непрерывно дифференцируемая функция \(U(x, y)\) (потенциал поля), что: \(P(x, y)\ dx + Q(x, y)\ dy = dU, P(x, y) = \frac{\partial U(x, y)}{\partial x},\quad Q(x, y) = \frac{\partial U(x, y)}{\partial y}.\)
В процессе доказательства данной теоремы следует придерживаться круговой схемы: \(1.\Rightarrow 2. \Rightarrow 3.\Rightarrow 1\).
Необходимо прийти к выводу, что:
- \(\Rightarrow 2.\)
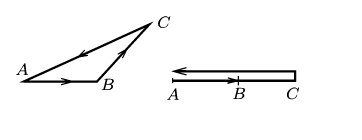
Допустим, первое условие выполнено. Следует задать пару произвольных точек A и B в области G и провести через них ломаную \(L_{AB}\). Предположим, что \(L’_{AB} \) является любой другой ломаной, которая соединяет точки A и B. В таком случае, \(L = L_{AB} + L’_{BA}\) представляет собой замкнутую ломаную. Согласно условию 1, получим:
\(0 = \int\limits_{L} P\ dx + Q\ dy = \int\limits_{L_{AB}} P\ dx + Q\ dy + \int\limits_{L’_{BA}} P\ dx + Q\ dy =\\= \int\limits_{L_{AB}} P\ dx + Q\ dy-\int\limits_{L’_{BA}} P\ dx + Q\ dy,\)
\(\int\limits_{L_{AB}} P\ dx + Q\ dy = \int\limits_{L’_{BA}} P\ dx + Q\ dy\)
Таким образом, интеграл \(\nonumber\int\limits_{L_{AB}} P\ dx + Q\ dy\) не зависит от ломаной \(L_{AB}\), которая соединяет точки \(A\) и \(B\).
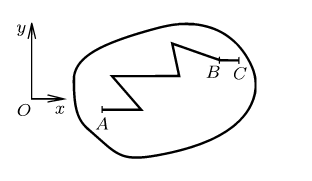
Затем необходимо доказать второе утверждение \(2. \Rightarrow 3\). Допустим, что \(\displaystyle\int\limits_{L_{AB}} P\ dx + Q\ dy\) не зависит от ломаной \(L_{AB}\), соединяющей точки \(A\) и \(B\). Определим точку \(A(x_{0}, y_{0})\), а точку \(B(x, y)\) можно принять за переменную. В таком случае, \(\displaystyle\int\limits_{L_{AB}} P\ dx + Q\ dy \) зависит лишь от точки B. Можно сделать вывод о том, что в области \(G\) определена функция:
\(U(x, y) = \int\limits_{L_{AB}} P\ dx + Q\ dy\).
Продемонстрируем, что функция \(U(x, y)\) является потенциалом поля. Можно соединить точки \(B(x, y) и C(x + \Delta x, y)\) с помощью отрезка \(BC\), который принадлежит области \(G\), как показано на рисунке. Данные действия выполнимы, если \Delta x является достаточно малым, так как \(G\) представляет собой открытое множество. Таким образом:
\(\frac{1}{\Delta x} (u(x + \Delta x, y)-U(x, y)) = \frac{1}{\Delta x} \left[\int\limits_{L_{ABC}} P\ dx + Q\ dy-\int\limits_{L_{AB}} P\ dx + Q\ dy\right] =\\= \frac{1}{\Delta x} \int\limits_{BC} P\ dx + Q\ dy = \frac{1}{\Delta x} \int\limits_{x}^{x + \Delta x} P(\xi, y) d\xi.\)
Далее следует использовать интегральную теорему о среднем для непрерывной функции \(P(\xi, y)\):
\(\frac{1}{\Delta x} (U(x + \Delta x, y)-U(x, y)) = P(x + \theta \Delta x, y),\ \mbox{где}\ 0 < \theta < 1\).
С помощью непрерывности функции \(P(x, y)\) и перехода к пределу при \(\Delta x \rightarrow 0\), получим:
\(\lim_{\Delta x \rightarrow 0} \frac{U(x + \Delta x, y)-U(x, y)}{\Delta x} = P(x, y) = \frac{\partial U}{\partial x}\).
Аналогичным способом подтверждается, что:
\(\displaystyle\frac{\partial U}{\partial y} = Q(x, y)\).
Исходя из того, что \(P(x, y) и Q(x, y)\) являются непрерывными в области \(G \) функции, функция \(U(x, y)\) непрерывно дифференцируема в области \(G\).
Представим доказательства 3. \(\Rightarrow 1\). Данный факт вытекает из более общего утверждения: при \(P(x, y)\ dx + Q(x, y)\ dy = dU\) для любого кусочно гладкого контура \(\gamma\) справедливо равенство:
\(\displaystyle\int\limits_{\gamma} P\ dx + Q\ dy = 0.\)
В действительности, если при \(x = x(t),\ y = y(t),\ \alpha \leq t \leq \beta\) существует уравнение кривой \(\gamma\), то:
\(\int\limits_{\gamma} P\ dx + Q\ dy = \int\limits_{\alpha}^{\beta} [P(x(t), y(t))x'(t) + Q(x(t), y(t))y'(t)] dt =\\= \int\limits_{\alpha}^{\beta} \left[\frac{\partial U}{\partial x} (x(t), y(t))x'(t) + \frac{\partial U}{\partial y} Q(x(t), y(t))y'(t)\right] dt =\\= \int\limits_{\alpha}^{\beta} \frac{d}{dt} [U(x(t), y(t))] dt = U(x(\beta), y(\beta))-U(x(\alpha), y(\alpha)) = 0\)
Записанное выражение следует из совпадения начала и конца замкнутой кривой.
При \(\displaystyle\int\limits_{\gamma} P\ dx + Q\ dy\) с нулевым значением по какой-либо замкнутой ломаной данный интеграл равен нулю и по любому кусочно гладкому контуру \(\gamma\).
Представим, что \(\displaystyle\int\limits_{L} P\ dx + Q\ dy = 0\) для любой замкнутой ломаной \(L. В\) таком случае, имеется потенциал \(U(x, y)\) и справедливо равенство:
\(P\ dx + Q\ dy = \frac{\partial U}{\partial x} (x, y)\ dx + \frac{\partial U}{\partial y} (x, y)\ dy\).
Из этого следует, что:
\(\displaystyle\int\limits_{\gamma} P\ dx + Q\ dy = 0.\)
С помощью рассмотренной теоремы нет возможности установить на практике потенциальность поля \(P, Q\). Для односвязной области \(G\) следует доказать эффективный критерий, который построен на основании формулы Грина.
Для того чтобы дифференцируемое в области \(G\) поле было потенциальным, необходимо (а в случае односвязной области и достаточно), чтобы выполнялось условие: \(\frac{\partial P(x, y)}{\partial y} = \frac{\partial Q(x, y)}{\partial x}.\)
В первую очередь следует доказать необходимость условия. Допустим, что поле \( (P(x, y), Q(x, y))\) непрерывно дифференцируемо и потенциально. В таком случае:
\(P(x, y) = \frac{\partial U(x, y)}{\partial x},\quad Q(x, y) = \frac{\partial U(x, y)}{\partial y}\)
Из записанного выражения следует:
\(\frac{\partial Q(x, y)}{\partial x} = \frac{\partial^{2} U(x, y)}{\partial x \partial y},\quad \frac{\partial P(x, y)}{\partial y} = \frac{\partial^{2} U(x, y)}{\partial y \partial x}.\)
Исходя из того, что производные \(\partial P/\partial y и \partial Q/\partial x\) являются непрерывными, смешанные производные \(U_{xy}, U_{yx}\) также непрерывны, а следовательно, равны. Первое условие теоремы выполняется для области \(G\).
Далее можно определить достаточность условия. Предположим, что поле \( P, Q\) задано в односвязной области \(G \subset \boldsymbol{R}^{2}\) и выполнено условие теоремы. Зададим некую простую замкнутую ломаную \(L \subset G\). Исходя из того, что область \(G\) является односвязной, ограничиваемая ломаной \(L\) область \(\Omega \subset G\), и к ней применима формула Грина:
\(\int\limits_{L} P\ dx + Q\ dy = \int\limits_{\Omega} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\ dx\ dy = 0.\)
В результате рассматриваемый интеграл будет иметь нулевое значение для любой простой замкнутой ломаной \(L\). Далее можно определить, что этот интеграл равен нулю в случае любой замкнутой ломаной, даже имеющей точки самопересечения.
В случае трехзвенной ломаной интеграл всегда обладает нулевым значением при условии, что рассматриваемая ломаная является замкнутой. При условии, что три вершины ломаной не располагаются на одной прямой, она является простой: согласно доказательствам, интеграл равен нулю. В том случае, когда все три вершины лежат на одной прямой, интеграл также обладает нулевым значением.
С помощью индукции по количеству звеньев ломаной можно доказать, что интеграл равен нулю для любой n-звенной замкнутой ломаной. Предположим, что интеграл обладает нулевым значением по любой замкнутой ломаной, количество звеньев которой меньше, чем \(n\). В таком случае, нужно показать, что криволинейный интеграл равен нулю и по любой замкнутой \(n\)-звенной ломаной.
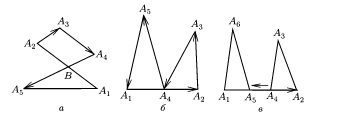
В случае, когда ломаная\( L(A_{1}, A_{2}, \ldots, A_{n}, A_{1})\) простая, данное утверждение доказано. Допустим, что \(L\) имеет точки самопересечения. Представим, что два звена, \(A_{1}A_{2} \)и \(A_{k}A_{k + 1}\), пересекаются. В таком случае, либо они пересекаются в единственной точке В, либо эти два звена пересекаются по целому отрезку. При этом точки \(A_{1}, A_{2}, A_{k}, A_{k + 1}\) расположены на одной прямой.
На рисунке в случаях а) и б) ломаная \(L\) объединяет замкнутые ломаные \(L_{1}(B, A_{k + 1}, \ldots, A_{n}, A_{1}, B) \) и \(L_{2}(B, A_{2}, \ldots, A_{k}, B)\). Количество звеньев \(L_{1} и L_{2}\) меньше, чем n. Согласно предположению индукции, интеграл по каждой из этих ломаных имеет нулевое значение. Таким образом, интеграл равен нулю и по их объединению в виде ломаной \(L\).
Аналогичным способом можно рассмотреть второй случай, при котором точки \(A_{1}, A_{2}, A_{k}, A_{k + 1}\) расположены на одной прямой, и отрезки \(A_{1}A_{2}\) и \(A_{k}A_{k + 1} \)обладают точками пересечения. Не ограничивая общность, можно прийти к выводу, что точка \(A_{k}\) расположена на отрезке \(A_{1}A_{2}\).
В таком случае,\( L\) является объединением замкнутых ломаных \(L_{1}(A_{k}, A_{k + 1}, \ldots, A_{n}, A_{1}, A_{k})\) и \(L_{2}(A_{k}, A_{2}, \ldots, A_{k-1}, A_{k})\), которые обладают неким количеством звеньев, меньшим, чем \(n\). Интеграл по \(L_{1}\) и \(L_{2}\) имеет нулевое значение. Таким образом, интеграл равен нулю и по ломаной \(L\).
Исходя из того, что интеграл равен нулю по любой замкнутой ломаной \(L \subset G\), согласно первой доказанной теореме, поле \((P, Q)\) будет потенциальным. Следует заметить, что условие односвязности области существенно для справедливости второй теоремы, что легко подтвердить с помощью решения практической задачи.
Требуется доказать, что непрерывно дифференцируемое при \(x^{2} + y^{2} > 0\) плоское векторное поле:
\(P(x, y) = -\frac{\omega}{2\pi} \frac{y}{x^{2} + y^{2}},\quad Q(x, y) = \frac{\omega}{2\pi} \frac{x}{x^{2} + y^{2}}\)
не является потенциальным при \(\omega \neq 0\) и соответствует условию:
\(\frac{\partial P(x, y)}{\partial y} = \frac{\partial Q(x, y)}{\partial x}\)
Указанное в задаче условие выполнимо, так как:
\(\frac{\partial P}{\partial y} = \frac{\omega}{2\pi} \frac{y^{2}-x^{2}}{(y^{2} + x^{2})^{2}} = \frac{\partial Q}{\partial x}.\)
Допустим, что имеется некая окружность \(C_{R}\), которую описывают уравнения:
\(x = R \cos t,\)
\(y = R \sin t, 0 \leq t \leq 2\pi.\)
В таком случае:
\(\int\limits_{C_{R}} P\ dx + Q\ dy = \frac{\omega}{2\pi} \int\limits_{C_{R}} \frac{x\ dy-y\ dx}{x^{2} + y^{2}} = \frac{\omega}{2\pi} \int\limits_{0}^{2\pi} dt = \omega\)
Согласно первой теореме, поле \((P, Q)\) не может быть потенциальным. Вторая теорема не может быть применена, так как поле определено в неодносвязной области:
\(G = \{(x, y): x^{2} + y^{2} > 0\}.\)
В гидродинамике рассмотренное поле определяют в виде поля скоростей точечного вихря, который расположен в точке \((0, 0)\) и имеет интенсивность \(\omega\). При переходе к полярным координатам r, \(\varphi\): \(v = (p, Q) = \frac{\omega}{2\pi r} (-\sin \varphi, \cos \varphi).\)
В физике жидкие частицы вращаются по концентрическим окружностям с постоянными скоростями, обратно пропорциональными расстоянию от точечного вихря.
Вычисление криволинейных интегралов разного типа с помощью формулы Грина
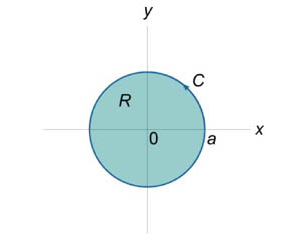
Требуется определить интеграл \(\oint\limits_C {xydx + \left( {x + y} \right)dy}\), где кривая C является окружностью радиуса R.
Решение
На первом этапе следует записать компоненты векторного поля:
\(P\left( {x,y} \right) = xy,\;\;Q\left( {x,y} \right) = x + y.\)
Используя формулу Грина, получим:
\({\iint\limits_R {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)dxdy} } = {\oint\limits_C {Pdx + Qdy} }\)
Преобразование криволинейного интеграла в двойной имеет вид:
\({I = \oint\limits_C {xydx + \left( {x + y} \right)dy} } = {\iint\limits_R {\left( {\frac{{\partial \left( {x + y} \right)}}{{\partial x}} - \frac{{\partial \left( {xy} \right)}}{{\partial y}}} \right)dxdy} } = {\iint\limits_R {\left( {1 - x} \right)dxdy} .}\)
При переходе к полярным координатам, можно рассчитать искомый интеграл:
\({I = \int\limits_R {\left( {1 - x} \right)dxdy} } = {\int\limits_0^{2\pi } {\int\limits_0^1 {\left( {1 - r\cos \theta } \right)rdrd\theta } } } = {\int\limits_0^{2\pi } {\left[ {\int\limits_0^1 {\left( {r - {r^2}\cos \theta } \right)dr} } \right]d\theta } } = {\int\limits_0^{2\pi } {\left[ {\left. {\left( {\frac{{{r^2}}}{2} - \frac{{{r^3}}}{3}\cos \theta } \right)} \right|_{r = 0}^1} \right]d\theta } } = {\int\limits_0^{2\pi } {\left( {\frac{1}{2} - \frac{{\cos \theta }}{3}} \right)d\theta } } = {\left. {\left( {\frac{\theta }{2} - \frac{{\sin \theta }}{3}} \right)} \right|_0^{2\pi } = \pi .}\)
Ответ: \(\pi\)
С помощью формулы Грина нужно вычислить интеграл \(\oint\limits_C {\left( {x - y} \right)dx + \left( {x + y} \right)dy}\), где кривая C является окружностью, которая задана уравнением: \({x^2} + {y^2} = {a^2}\).
Решение
Компоненты векторного поля можно записать таким образом:
\(P = x - y,\;\;Q = x + y\)
Далее следует рассчитать частные производные:
\({\frac{{\partial Q}}{{\partial x}} = \frac{{\partial \left( {x + y} \right)}}{{\partial x}} = 1,}\;\; {\frac{{\partial P}}{{\partial y}} = \frac{{\partial \left( {x - y} \right)}}{{\partial x}} = - 1.}\)
В результате получим интеграл в виде:
\({I = \oint\limits_C {\left( {x - y} \right)dx + \left( {x + y} \right)dy} } = {\iint\limits_R {\left( {1 - \left( { - 1} \right)} \right)dxdy} } = {2\iint\limits_R {dxdy} .}\)
Последнее выражение содержит двойной интеграл \(\iint\limits_R {dxdy}\), который численно равен площади круга \({x^2} + {y^2} = {a^2}\). Таким образом, интеграл соответствует \(\pi {a^2}\):
\(I = 2\iint\limits_R {dxdy} = 2\pi {a^2}\)
Ответ: \(2\pi {a^2}\)
Необходимо определить интеграл \(\oint\limits_C {{x^2}ydx - x{y^2}dy}\). Кривая C является окружностью \({x^2} + {y^2} = {a^2}\) (рисунок 1), обход которой производится против часовой стрелки, как показано на рисунке:
Решение
В первую очередь следует записать компоненты векторного поля и их производные:
\({P\left( {x,y} \right) = {x^2}y,}\;\; {Q\left( {x,y} \right) = - x{y^2},}\;\; {\frac{{\partial Q}}{{\partial x}} = \frac{{\partial \left( { - x{y^2}} \right)}}{{\partial x}} = - {y^2},}\;\; {\frac{{\partial P}}{{\partial y}} = \frac{{\partial \left( {{x^2}y} \right)}}{{\partial y}} = {x^2}.}\)
В таком случае:
\({I = \oint\limits_C {{x^2}ydx - x{y^2}dy} } = {\iint\limits_R {\left( { - {y^2} - {x^2}} \right)dxdy} } = { - \iint\limits_R {\left( {{x^2} + {y^2}} \right)dxdy} ,}\)
где R является кругом радиуса \(r=a\) с центром в начале координат.
При переходе к полярным координатам, можно определить искомый интеграл:
\({I = - \iint\limits_R {\left( {{x^2} + {y^2}} \right)dxdy} } = { - \int\limits_0^{2\pi } {d\theta } \int\limits_0^a {\left( {{r^2}{{\cos }^2}\theta + {r^2}{\sin^2}\theta } \right)rdr} } = { - \int\limits_0^{2\pi } {d\theta } \int\limits_0^a {{r^3}dr} } = { - 2\pi \cdot \left[ {\left. {\left( {\frac{{{r^4}}}{4}} \right)} \right|_0^a} \right] } = { - \frac{{\pi {a^4}}}{2}.}\)
Ответ: \(- \frac{{\pi {a^4}}}{2}\)
Нужно найти интеграл \(\oint\limits_C {\left( {x + y} \right)dx - \left( {x - y} \right)dy}\), где кривая \(C \) является эллипсом:
\(\large\frac{{{x^2}}}{{{a^2}}}\normalsize + \large\frac{{{y^2}}}{{{b^2}}}\normalsize = 1\)
Решение
Согласно формуле Грина:
\({\oint\limits_C {Pdx + Qdy} } = { \iint\limits_R {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)dxdy} . }\)
Таким образом:
\({P = x + y,}\;\; {Q = - \left( {x - y} \right),}\;\; {\frac{{\partial Q}}{{\partial x}} = - 1,}\;\; {\frac{{\partial P}}{{\partial y}} = 1.}\)
В результате получим:
\({I = \oint\limits_C {\left( {x + y} \right)dx - \left( {x - y} \right)dy} } = {\iint\limits_R {\left( { - 1 - 1} \right)dxdy} } = { - 2\iint\limits_R {dxdy} .}\)
Так как двойной интеграл \(\iint\limits_R {dxdy}\) численно равен площади эллипса \pi ab, то интеграл определяется, как:
\(I = - 2\iint\limits_R {dxdy} = - 2\pi ab\)
Ответ: \(- 2\pi ab\)
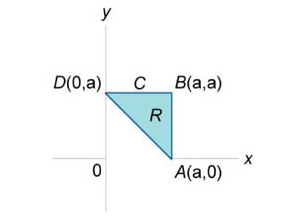
Требуется найти интеграл \(\oint\limits_C {{y^2}dx + {{\left( {x + y} \right)}^2}dy}\), где контур \(C\) является треугольником \(ABC\) с вершинами:
\(A\left( {a,0} \right)\);
\(B\left( {a,a} \right);\)
\(D\left( {0,a} \right).\)
Решение
В рассматриваемом криволинейном интеграле \(P = {y^2}, Q = {\left( {x + y} \right)^2}\). Таким образом:
\({\frac{{\partial Q}}{{\partial x}} = \frac{{\partial \left( {{{\left( {x + y} \right)}^2}} \right)}}{{\partial x}} = 2\left( {x + y} \right),}\;\; {\frac{{\partial P}}{{\partial y}} = \frac{{\partial \left( {{y^2}} \right)}}{{\partial y}} = 2y.}\)
Согласно формуле Грина:
\({I = \oint\limits_C {{y^2}dx + {{\left( {x + y} \right)}^2}dy} } = {\iint\limits_R {\left[ {2\left( {x + y} \right) - 2y} \right]dxdy} } = {2\iint\limits_R {xdxdy} .}\)
Уравнение стороны \(AD\):
\(y = -x + a.\)
В результате полученный двойной интеграл можно определить:
\({I = 2\iint\limits_R {xdxdy} } = {2\int\limits_0^a {\left[ {\int\limits_{ - x + a}^a {dy} } \right]xdx} } = {2\int\limits_0^a {\left[ {\left. y \right|_{ - x + a}^a} \right]xdx} } = {2\int\limits_0^a {\left[ {a - \left( { - x + a} \right)} \right]xdx} } = {2\int\limits_0^a {{x^2}dx} } = {2\left[ {\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^a} \right] } = {\frac{{2{a^3}}}{3}.}\)
Ответ: \(\frac{{2{a^3}}}{3}\)
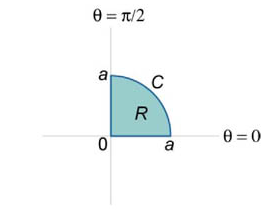
Необходимо вычислить интеграл \(\oint\limits_C {\left( {y - {x^2}} \right)dx - \left( {x + {y^2}} \right)dy}\). Контур \(C\) ограничивает сектор круга, лежащий в первом квадранте, радиус которого \(r=a\).
Согласно формуле Грина:
\({\oint\limits_C {Pdx + Qdy} } = { \iint\limits_R {\left( {\frac{{\partial Q}}{{\partial x}} - \frac{{\partial P}}{{\partial y}}} \right)dxdy}, }\)
Далее следует определить:
\({P = y - {x^2},}\;\; {Q = - \left( {x + {y^2}} \right),}\;\; {\frac{{\partial Q}}{{\partial x}} = - \frac{{\partial \left( {x + {y^2}} \right)}}{{\partial x}} = - 1,}\;\; {\frac{{\partial P}}{{\partial y}} = \frac{{\partial \left( {y - {x^2}} \right)}}{{\partial y}} = 1.}\)
Таким образом:
\({I = \oint\limits_C {\left( {y - {x^2}} \right)dx - \left( {x + {y^2}} \right)dy} } = {\iint\limits_R {\left( { - 1 - 1} \right)dxdy} } = { - 2\iint\limits_R {dxdy} .}\)
При переходе к полярным координатам можно вычислить интеграл:
\({I = - 2\iint\limits_R {dxdy} } = { - 2\int\limits_0^{\large\frac{\pi }{2}\normalsize} {d\theta } \int\limits_0^a {rdr} } = { - 2 \cdot \frac{\pi }{2} \cdot \left[ {\left. {\left( {\frac{{{r^2}}}{2}} \right)} \right|_0^a} \right] } = { - \frac{{\pi {a^2}}}{2}.}\)
Ответ:\( - \frac{{\pi {a^2}}}{2}\)
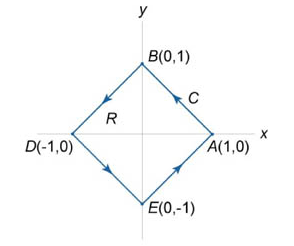
Требуется рассчитать значение интеграла \(\oint\limits_C {\large\frac{{dx - dy}}{{x + y}}\normalsize}\). Контур интегрирования \(C\) является геометрической фигурой — квадратом, с вершинами в точках:
\(A\left( {1,0} \right)\);
\(B\left( {0,1} \right)\);
\(D\left( {-1,0} \right)\);
\(E\left( {0,-1} \right)\).
Решение
Согласно теории формулы Грина:
\({P = \frac{1}{{x + y}},}\;\; {Q = - \frac{1}{{x + y}},}\;\; {\frac{{\partial Q}}{{\partial x}} = \frac{{\partial \left( { - \frac{1}{{x + y}}} \right)}}{{\partial x}} = \frac{1}{{{{\left( {x + y} \right)}^2}}},}\;\; {\frac{{\partial P}}{{\partial y}} = \frac{{\partial \left( {\frac{1}{{x + y}}} \right)}}{{\partial y}} = - \frac{1}{{{{\left( {x + y} \right)}^2}}}.}\)
Таким образом:
\({I = \oint\limits_C {\frac{{dx - dy}}{{x + y}}} } = {\iint\limits_R {\left( {\frac{1}{{{{\left( {x + y} \right)}^2}}} + \frac{1}{{{{\left( {x + y} \right)}^2}}}} \right)dxdy} } = {2\iint\limits_R {\frac{{dxdy}}{{{{\left( {x + y} \right)}^2}}}} .}\)
Далее следует записать уравнения для сторон квадрата:
\(AB:y = - x + 1\),
\(BD:y = x + 1\),
\(DE:y = - x - 1\),
\(EA:y = x - 1.\)
Затем целесообразно ввести новые переменные. Допустим, что:
\(u = y + x,\)
\(v = y - x.\)
Уравнения сторон квадрата можно записать с помощью новых переменных \(u\) и \(v\) в виде:
\(y = - x + 1,\;\; \Rightarrow y + x = 1,\;\; \Rightarrow u = 1,\)
\(y = x + 1,\;\; \Rightarrow y - x = 1,\;\; \Rightarrow v = 1,\)
\(y = - x - 1,\;\; \Rightarrow y + x = - 1,\;\; \Rightarrow u = - 1,\)
\(y = x - 1,\;\; \Rightarrow y - x = - 1,\;\; \Rightarrow v = - 1.\)
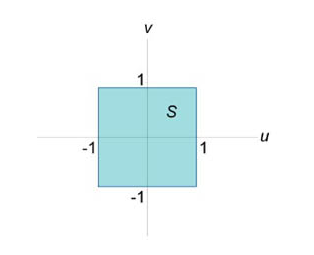
В результате полученный образ \(S\) первоначальной области интегрирования \(R \) стал более удобным для расчетов с квадратом:
Определим якобиан обратного преобразования координат:
\({\frac{{\partial \left( {u,v} \right)}}{{\partial \left( {x,y} \right)}} } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial u}}{{\partial x}}}&{\frac{{\partial u}}{{\partial y}}}\\ {\frac{{\partial v}}{{\partial x}}}&{\frac{{\partial v}}{{\partial y}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} {\frac{{\partial \left( {y + x} \right)}}{{\partial x}}}&{\frac{{\partial \left( {y + x} \right)}}{{\partial y}}}\\ {\frac{{\partial \left( {y - x} \right)}}{{\partial x}}}&{\frac{{\partial \left( {y - x} \right)}}{{\partial y}}} \end{array}} \right| } = {\left| {\begin{array}{*{20}{c}} 1&1\\ { - 1}&1 \end{array}} \right| = 2.}\)
Таким образом, абсолютное значение якобиана прямого преобразования определяется как:
\({\left| {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}} \right| } = {\left| {{{\left( {\frac{{\partial \left( {u,v} \right)}}{{\partial \left( {x,y} \right)}}} \right)}^{ - 1}}} \right| = \frac{1}{2}.}\)
В результате анализа:
\(dxdy = \left| {\frac{{\partial \left( {x,y} \right)}}{{\partial \left( {u,v} \right)}}} \right|dudv = \frac{1}{2}dudv\)
Значение интеграла:
\({I = 2\iint\limits_R {\frac{{dxdy}}{{{{\left( {x + y} \right)}^2}}}} } = {2\iint\limits_S {\frac{{\frac{1}{2}dudv}}{{{u^2}}}} } = {\iint\limits_S {\frac{{dudv}}{{{u^2}}}} } = {\int\limits_{ - 1}^1 {dv} \int\limits_{ - 1}^1 {\frac{{du}}{{{u^2}}}} } = {\left[ {\left. v \right|_{ - 1}^1} \right] \cdot \left[ {\left. {\left( { - \frac{1}{u}} \right)} \right|_{ - 1}^1} \right] } = {\left[ {1 - \left( { - 1} \right)} \right] \cdot \left[ { - 1 - \left( { - 1} \right)} \right] = - 4.}\)
Ответ: -4
Источник: www.math24.ru
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так