Ве формулы для окружности в геометрии

Что такое окружность — определение и свойства

Окружность обладает рядом характерных свойств:

1. Диаметр окружности в два раза больше, чем радиус окружности: D = 2r.
2. Минимальное расстояние от центра окружности к секущей (хорде) в любом случае меньше, чем радиус окружности.
3. Если существуют три точки, расположенные не на одной прямой, то через них можно провести единственно возможную окружность.
4. Из всех замкнутых кривых, обладающих аналогичной длиной, окружность обладает максимально возможной площадью.
5. При соприкосновении пары окружностей в определенной точке, эта точка расположена на прямой, которая проходит через центры заданных окружностей.

Через какие параметры ее можно найти

Окружность, радиус которой равен r, а центр совпадает с началом декартовой системы координат, можно описать уравнением:

\(r^{2}=x^{2}+y^{2}\)

Данная формула в алгебре является основной.

Если имеется окружность, радиус которой равен r, а центр совпадает с точкой, имеющей координаты (a, b) в декартовой системе координат, то уравнение рассматриваемой окружности приобретает следующий вид:

\(r^{2}=(x-a)^{2}+(y-b)^{2} \)

Параметрическое уравнение окружности, которая имеет радиус r и центр в точке с координатами (a, b) в декартовой системе координат, записывают следующим образом:

\(\begin{cases}x = a + r cos t\\y = b + r sin t\end{cases} \)

Формула длины окружности

Длину окружности можно определить, зная ее диаметр:

\(L = \pi D\)

При известном радиусе длину окружности можно вычислить по формуле:

\(L = 2\pi r\)

Формула диаметра окружности

Существует две формулы для определения диаметра окружности через радиус и длину:

\(d = 2 * R\)

\(d = \frac{C}{\pi}\)

Формула радиуса окружности

Радиус окружности можно определить двумя способами через диаметр и длину:

\(R = \frac{d}{2}\)

\(R = \frac{C}{2\pi}\)

Примеры задач с решением

Задача 1

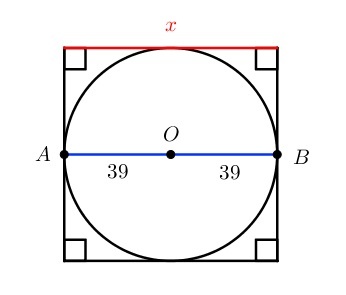
Существует некая окружность, вписанная в квадрат, радиус которой равен 39. Необходимо рассчитать площадь квадрата, представленного на графике.

Решение

Сначала требуется построить радиусы ОА и ОВ к точке, в которой окружность касается с квадратом.

Отрезок АВ можно определить, как сторону квадрата.

х = АВ = 39 + 39 = 78

Площадь квадрата:

\(S = x^{2} = 78^{2} = 6084\)

Ответ: площадь квадрата составляет 6084.

Задача 2

Диаметр окружности равен 5 см. Необходимо определить, какова длина заданной окружности.

Решение

Длину окружности можно рассчитать по формуле:

\(L = \pi D\)

Исходя из условий задачи, подставим значение диаметра в уравнение и выполним вычисления:

L = 3,14 * 5 = 15,7 (см)

Ответ: длина окружности равна 15,7 см.

Задача 3

Существует окружность с радиусом 3,5 м. Требуется определить длину данной окружности.

Решение

В первую очередь следует определить величину диаметра рассматриваемой окружности:

D = 2r = 3,5 * 2 = 7 (м)

Далее можно рассчитать длину окружности:

\(L = \pi D = 3,14 * 7 = 21,98 (м)\)

Ответ: длина окружности составляет 21,98 м.

Задача 4

Длина окружности составляет 7,85 м. Требуется определить радиус этой окружности.

Решение

Рассчитать радиус окружности, зная ее длину, можно путем деления длины на \(2\pi:\)

\(R = \frac{C}{2\pi}\)

Таким образом:

\(R = \frac{7,85}{2 * 3,14} = \frac{7,85}{6,28} = 1,25 (м)\)

Ответ: радиус окружности равен 1,25 м.