Формулы приведения в тригонометрии

Что такое формулы приведения в тригонометрии

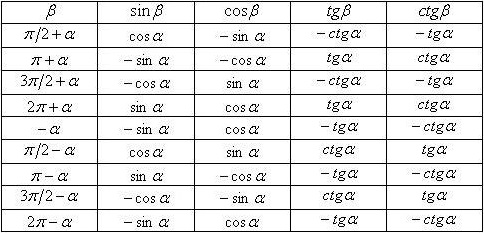
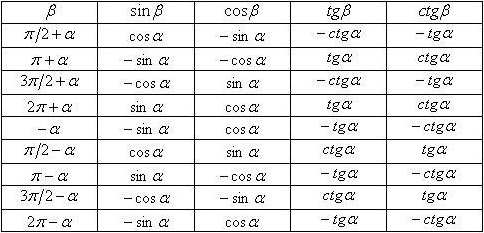
Список ФП:

Приведем доказательство данной теории. Заметим, что все ФП можно доказывать, отбросив при этом 2\pi\times z, потому что это число означает число полных оборотов, но значения никак не меняет.

Сначала докажем \(\sin\;\left(\frac\pi2+\alpha\right)=\cos\;\alpha\;и\;\cos\;\left(\frac\pi2+\alpha\right)=-\sin\;\alpha. \)

Рассмотрим единичную окружность.

В ней начальная точка А после на \(\angle\alpha\) переходит в точку А₁ (х, у), а после поворота на \(\angle\frac\pi2+\alpha\) — в точку А₂.

Если провести перпендикуляры А₁Н₁ и А₂Н₂ в прямой Ох, то можно увидеть, что получившиеся треугольники ОА₁Н₁ и А₂Н₂ равны по гипотенузе и прилежащим углам. Из равенства треугольников делаем вывод, что точка А₂ имеет координаты -у и х.

Тогда согласно определениям синуса и косинуса:

\(\sin\;\alpha=y,\;\cos\;\alpha=x,\;\sin\;\left(\frac\pi2+\alpha\right)=x,\;\cos\;\left(\frac\pi2+\alpha\right)=-y\)

Из этого:

\(\sin\;\left(\frac\pi2+\alpha\right)=\cos\;\alpha,\;\cos\;\left(\frac\pi2+\alpha\right)=-\sin\;\alpha\)

Если учесть, что

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}ф tg\;\left(\frac\pi2+\alpha\right)=\frac{\sin\;\left(\frac\pi2+\alpha\right)}{\cos\;\left(\frac\pi2+\alpha\right)}\;и\;ctg\;\left(\frac\pi2+\alpha\right)=\;\frac{\cos\;\left(\frac\pi2+\alpha\right)}{\sin\;\left(\frac\pi2+\alpha\right)}\)

и только что доказанные формулы, получим:

\(tg\;\left(\frac\pi2+\alpha\right)=\frac{\sin\;\left(\frac\pi2+\alpha\right)}{\cos\;\left(\frac\pi2+\alpha\right)}=\frac{\cos\;\alpha}{-\sin\;\alpha}=-ctg\;\alpha\;и\;ctg\;\left(\frac\pi2+\alpha\right)=\;\frac{\cos\;\left(\frac\pi2+\alpha\right)}{\sin\;\left(\frac\pi2+\alpha\right)}=\frac{-\sin\;\alpha}{\cos\;\alpha}=-tg\;\alpha\)

Так мы доказали еще одну ФП. Остальные следует доказывать и решать аналогичным путем.

Таблица значения тригонометрических функций для основных углов

Приведем таблицу, иллюстрирующую значения тригонометрических тождеств для часто встречающихся углов:

Примеры использования формул приведения

Для начало отметим, что существует довольно много способов представления угла под знаком тригонометрических функций в виде:

\(\pm\alpha+2\pi\times z,\;\frac\pi2\pm\alpha+2\pi\times z\;и\;\frac{3\pi}2\pm\alpha+2\pi\times z\)

Это обусловлено тем, что угол может принимать любое значение.

Например, возьмем угол \(\frac{16\pi}3\). Его можно представить как

\(\pi+\frac\pi3+2\pi\times2\)

или

\(-\frac{2\pi}3+2\pi\times3\)

или же

\(\frac{3\pi}2-\frac\pi6+2\pi\times2\)

Далее сравним, какие формулы приведения будут работать в зависимости от представления угла. Например, \(tg\;\frac{16\pi}3.\)

Если представить этот угол как \(\pi+\frac\pi3+2\pi\times2\), то ему будет соответствовать ФП вида:

\(\;\left(\pi+\alpha+2\pi\times z\right)=tg\;\alpha\)

Откуда получается:

\(tg\;\frac{16\pi}3=tg\;\left(\pi+\frac\pi3+2\pi\times2\right)=tg\;\frac\pi3\)

В таком случае можно указать значение ТФ:

\(tg\;\frac\pi3=\sqrt3\)

Для того, чтобы выразить \(-\frac{2\pi}3+2\pi\times3\) необходимо использовать следующую формулу:

\(tg\;\left(-\alpha+2\pi\times z\right)=-tg\;\alpha\)

Это равенство приводит к результату:

\(tg\;\frac{16\pi}3=tg\;\left(-\frac{2\pi}3+2\pi\times3\right)=-tg\;\left(\frac{2\pi}3\right)=-\left(-\sqrt3\right)=\sqrt3\)

Далее:

\(tg\;\frac{16\pi}3=tg\;\left(\frac{3\pi}2-\frac\pi6+2\pi\times2\right)=сtg\;\left(\frac\pi6\right)=\sqrt3\)

потому что соответствующая ФП имеет вид:

\(tg\;\left(\frac{3\pi}2-\alpha+2\pi\times z\right)\)

Рассмотрим объяснение еще одного примера, где используются ФП.

Задача

Представить \(\sin\;197^\circ\) через синус и косинус острого угла.

Решение

Для того, чтобы применить ФП, нужно заданный угол представить в виде:

\(\pm\alpha+360^\circ\times z,\;90^\circ\pm\alpha+360^\circ\times z,\;180^\circ\pm\alpha+360^\circ\times z\;или\;270^\circ\pm\alpha+360^\circ\times z\)

Важно не забывать, что угол острый. Тогда можно поступить двумя способами, то есть сложением или вычитанием:

\(197^\circ=180^\circ+17^\circ\;\)

или

\(\;197^\circ=270^\circ-73^\circ\)

Получается, что

\(\sin\;197^\circ=\sin\left(180^\circ+17^\circ\right)\;\)

или

\(\;197^\circ=\sin\left(270^\circ-73^\circ\right)\)

Обратимся к описанным выше ФП и получим:

\(\sin\;197^\circ=\sin\left(180^\circ+17^\circ\right)=-\sin\;17^\circ\;и\;\sin\;197^\circ=\sin\left(270^\circ-73^\circ\right)=-\cos\;73^\circ\)

Ответ: \(\sin\;197^\circ=-\sin\;17^\circ\;и\;\sin\;197^\circ=-\cos\;73^\circ.\)

Мнемоническое правило формул приведения, как их запомнить

Запомнить ФП можно с помощью вывода определенных закономерностей в них. Мнемоническое правило запоминания содержит алгоритм, состоящий из трех этапов:

1. Аргумент исходного выражения нужно представить таким образом: \(\;\pm\alpha+2\pi\times z,\;\pi\pm\alpha+2\pi\times z,\;\frac\pi2\pm\alpha+2\pi\times z\;и\;\frac{3\pi}2\pm\alpha+2\pi\times z\). При этом \(\angle\alpha\) должен находиться в промежутке от 0 до 90 градусов.
2. Дальше необходимо определить знак исходного уравнения. Функция в правой части ФП будет иметь тот же знак, что изначально.
3. Для углов \(\pm\alpha+2\pi\times z,\;\pi\pm\alpha+2\pi\times z\;\) название изначальной функции остается неизменным, а для \(\frac{3\pi}2\pm\alpha+2\pi\times z,\;\frac\pi2\pm\alpha+2\pi\times z\; \)название меняется на кофункцию. Это значит, что синус сменяется косинусом, косинус — синусом, тангенс — котангенсом и котангенс — тангенсом.