Функция тангенса: формула, свойства, график

Что такое тангенс

Понятие тангенса угла можно проиллюстрировать таким образом:

Источник: microexcel.ru

Что такое функция тангенса: формула

При решении задач можно нередко встретить примеры с тригонометрическими функциями, в том числе, функцией тангенса. Эта функция обладает специфическими свойствами, которые значительно упрощают вычисления. Запись имеет следующий вид:

\(у = tg х\)

Здесь х обозначает аргумент тригонометрической функции и играет роль независимой переменной, а у определяет непосредственно функцию, то есть зависимую переменную.

Свойства функции

С помощью знаний свойств функций в тригонометрии достаточно просто решать самые сложные и громоздкие примеры. Перечислим закономерности, характерные для функции тангенса:

1. Функция тангенса определяется в области \((x\ne\frac\pi2+\pi k)\), то есть на множестве, в состав которого включены действительные числа, за исключением точек, характеризующихся нулевым значением для косинуса.
2. Функция на графике не имеет ограничений в верхней и нижней части, поэтому ее область значений можно записать как \(y\in\mathbb{R}\).
3. Функция тангенса является нечетной, что целесообразно записать в виде соотношения \(tg(-x)=-tgx\).
4. Тригонометрическая функция тангенса является периодической, а ее период составляет pi. Таким образом:\(tg(x+\pi k)=tgx\) .
5. Стремление функции \(к +\infty\) можно наблюдать при сближении с левой стороны с точками \(x=\frac\pi2+\pi k\). Приближение к точке, обозначенной за a, слева формулируют таким образом: \(x\rightarrow\) \(a-0 \lim_{x\rightarrow\frac\pi2+\pi k-0} tgx=+\infty\) .
6. Стремление функции \(к -\infty\) можно наблюдать при сближении с правой стороны с точками \(x=\frac\pi2+\pi k\). Приближение к точке, обозначенной за а, справа следует зафиксировать как \(x\rightarrow\) \(a+0 \lim_{x\rightarrow\frac\pi2+\pi k+0} tgx=-\infty\).
7. Нули рассматриваемой функции \(y_{0}=0\) определены точками \(x_0=\pi k\).
8. Возрастание функции можно наблюдать на всей области, где она определена.
9. Функция разрывается в точках \(x=\frac\pi2+\pi k\), которые пересечены вертикальными асимптотами. На отрезках между ними функция не прерывается, то есть \(\left(-\frac\pi2+\pi k;\ \frac\pi2+\pi k\right).\)
10. Функция не обладает максимальными и минимальными значениями.

Как построить график

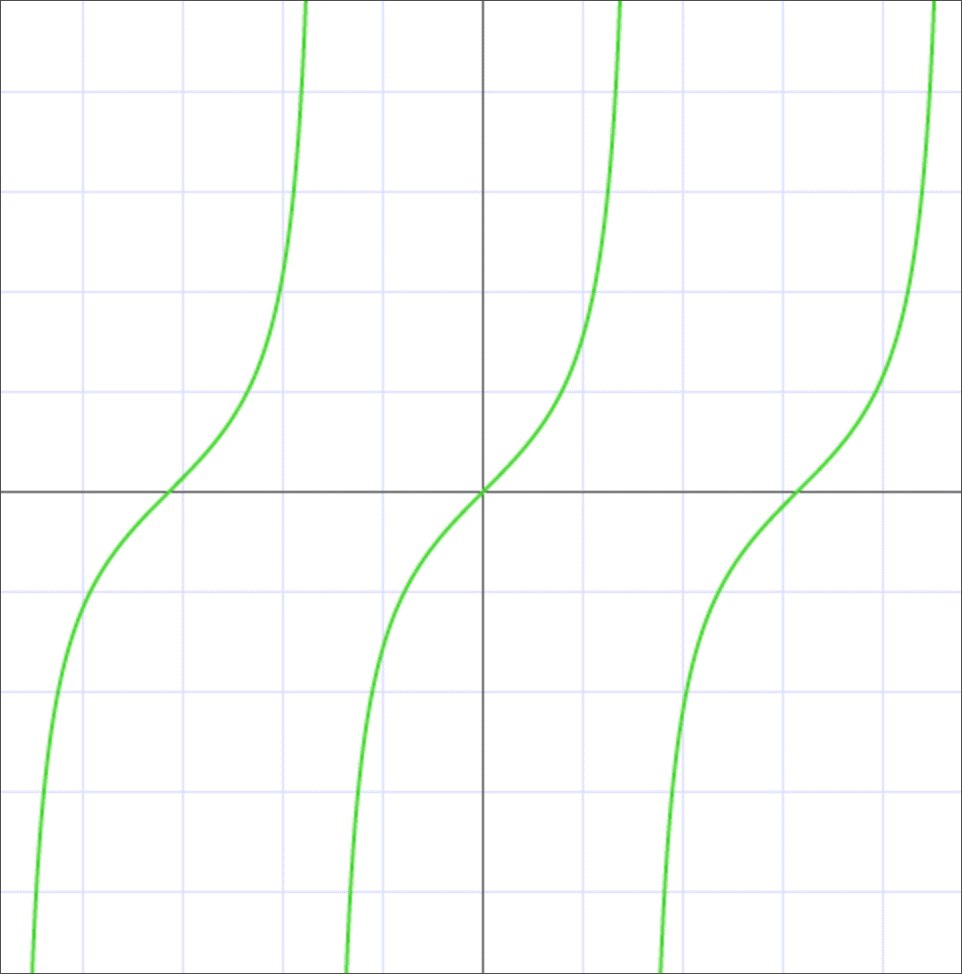
Как и любую другую тригонометрическую функцию, тангенс достаточно просто изобразить в системе координат. Графическое изображение функции тангенса в обобщенном виде представлено на рисунке ниже:

Источник: microexcel.ru

Построить график функции тангенса несложно. Нужно лишь последовательно выполнять действия согласно стандартному алгоритму:

• определить контрольные точки для построения;
• начертить плавную кривую линию на плоскости координат;
• для выбранного промежутка построить значения, которые расположены симметрично по отношению к началу координат;
• так как для значений функции характерны повторы с некоторым периодом, то целесообразно скопировать график для каждого из промежутков области определения;
• в результате получен график под названием тангенсоида.

Примеры решения задач

Решение

Зная, что функция тангенса не может быть определена в точках при нулевом значении косинуса, запишем справедливое соотношение и выполним необходимые преобразования:

\(\cos \left( 2x+\frac{\pi }{3} \right)=0\)

\(2x+\frac{\pi }{3}\ne \frac{\pi }{2}+\pi n,n\in Z\)

\(x\ne \frac{\pi }{12}+\frac{\pi n}{2},n\in Z\)

В результате получена область, в которой определена функция из условия задания:

\(D(y)=\left( -\frac{\pi }{12}+\frac{\pi n}{2},\frac{\pi }{12}+\frac{\pi n}{2} \right),n\in Z\)

Ответ: \(D(y):x\in \left( -\frac{\pi }{12}+\frac{\pi n}{2},\frac{\pi }{12}+\frac{\pi n}{2} \right),n\in Z\) 

Решение

Выполним преобразования исходного соотношения. В результате получим:

\(\sin 2x=\sqrt{3}\cos 2x\)

После деления всех частей записи на выражение \(\cos 2x\) соотношение изменится таким образом:

\(\text{tg}2x=\sqrt{3}\)

При этом ОДЗ для полученного выражения примет следующий вид:

\(\left( -\frac{\pi }{4}+\frac{\pi n}{2},\frac{\pi }{4}+\frac{\pi n}{2} \right),n\in Z.\)

Далее целесообразно приступить к решению уравнения:

\(2=\frac{\pi }{3}+\pi n,n\in Z\)

\(x=\frac{\pi }{6}+\frac{\pi n}{2},n\in Z\)

Заметим, что корни, которые получились по итогам расчетов, соответствуют ОДЗ. Можно записать ответ.

Ответ: \(x=\frac{\pi }{6}+\frac{\pi n}{2},n\in Z\)