Функция обратной пропорциональности

Какая функция называется обратной пропорциональностью

Исходя из данного описания, во сколько раз увеличивается аргумент, во столько же раз уменьшается функция, и, наоборот, во сколько раз уменьшается аргумент, во столько же раз увеличивается функция.

Функцию обратной пропорциональности можно записать на математическом языке так:

\(y=\frac kx\)

В данной формуле переменные x и k — не равно нулю.

Свойства обратно пропорциональной функции

1. Область определения — все действительные числа, кроме значения x, равного нулю, то есть промежуток D(x):(−∞; 0) U (0; +∞).
2. Множество значений — все числа, исключая y=0, то есть: E(y):(−∞; 0) U (0; +∞).
3. У функции отсутствуют максимальное и минимальное значения.
4. Функция нечетная, ее график симметричен по отношению к точке (0; 0), то есть началу координат.
5. Функция неповторяющаяся, следовательно, не является периодической.
6. График не пересекает оси абсцисс и ординат.
7. Функция не имеет 0.
8. При k>0 у функции y=k/x на промежутках от −∞ до 0 и от 0 до +∞ наблюдается убывание. При k<0 у функции y=k/x на промежутках от −∞ до 0 и от 0 до +∞ наблюдается возрастание.
9. y=k/x (k>0) на промежутке от −∞ до 0 отрицательна, а на участке от 0 до +∞ — положительна. y=k/x (k<0) на участке (0; +∞) — меньше нуля, а на промежутке (−∞; 0) — больше нуля.

Что представляет собой график обратно пропорциональной зависимости

График функции y=k/x при x≠0 и y≠0 имеет вид гиперболы.

Ветви гиперболы лежат в разных четвертях системы координат симметрично по отношению к началу координат (0; 0). Если коэффициент k принимает значения, больше нуля, то компоненты диаграммы располагаются в первой и третьей четвертях, если k меньше нуля — во второй и четвертой.

Особенности построения, пример

Пусть, функция задана формулой:

\(y=\frac3x\)

1. Так как коэффициент 3 положительный, то гипербола расположится в 1 и 3 четвертях.
2. Вычислим значения y, задав произвольные значения независимой переменной x. Так определим координаты точек, по которым произведем построение графика. Напомним, что x и y не должны ровняться нулю.
3. Так как ветви гиперболы располагаются в двух четвертях, возьмем абсциссы больше 0 (x=1, x=2, x=3, x=6) и меньше 0 (x=−1, x=−2, x=−3, x=−6).
4. Далее вычислим ординаты, подставив выбранные значения x в исходное уравнение: у=3/1=3; y=3/2= 1,5; у=3/3=1; у=3/6=0,5; у=3/−1=−3; y=3/−2=−1,5; у=3/−3=−1; y=3/−6=−0,5.
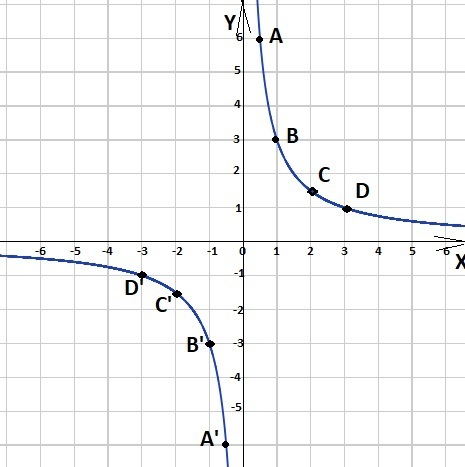
5. В результате предыдущих математических операций получилось восемь точек с координатами: A(6; 0,5), B(3; 1), C(2; 1,5), D(1; 3), A₁(−6; −1/2), B₁(−3; −1), C₁(−2; −1,5), D₁(−1; −3). Плавно проведем через них кривые и получим график заданной функции: