Основные сведения о функции нескольких переменных

Общее определение

В случае функции двух переменных, рассматривается некоторое множество упорядоченных пар $\left(x,y\right)$, где \(x\in X,\;y\in Y\).

Она будет записываться следующим образом:

$z=z\left(x,y\right)$, $z=f\left(x,y\right)$, $z=F\left(x,y\right)$

$Функцию z = f(x,y)\; можно\; изобразить\; при\; помощи\; некоторой\; поверхности\; в\; пространстве\; в\; прямоугольной\; системе.\; Тогда\; область\; определения\; функции\; двух\; переменных\; будет\; представлять\; собой\; множество\; точек\; плоскости,\; в\; то\; же\; время\; область\; функции\; трех\; переменных\; будет\; представлять\; собой\; некоторое\; множество\; точек\; трехмерного\; пространства.$

Функция с любым иным количеством переменных (n) будет определяться аналогичным образом.

Функции нескольких переменных: основные определения

Для более полного понимания, рассмотрим понятия, которые используются для функции нескольких переменных.

Независимые переменные (x₁, x₂, x₃, x_n) являются аргументами функции.

U — область значений (обозначают: E(u));

u (\(u \in U\)) — зависимая переменная (функция).

Функцию нескольких переменных можно задать четырьмя разными способами:

• словесный;
• табличный;
• аналитический;
• графический.

Аналитический способ в свою очередь подразделяется на два варианта — явный и неявный. Явный способ задания функции нескольких переменных выглядит как формула u = f(x₁, x₂, x₃ ... x_n), в то время как при неявном способе используется уравнение F(x₁, x₂, x₃ ... x_n) = 0.

Графический способ — это начертание графика функции. Тогда график функции z = f(x,y) будет называться «поверхностью функции». В то время как непосредственное геометрическое место точек (x, y) на плоскости, в которых она принимает одно и то же значение С, будет называться «линией уровня функции z». 

• линия в D(z), имеющая уравнение f(x,y) = C будет называться линией функции;
• проекция на плоскость xOy линии пересечения графика функции z = f(x,y) и плоскости z = C будет называться линией функции.

С помощью этих линий и их распространения можно оценить характер изменения самой функции. В месте «густоты» линий она будет изменяться быстрее.

При этом существует также поверхность уровня функции u = f(x,y,z). Поверхностью называется геометрическое место точек пространства Oxyz, в которых функция принимает одно и то же значение C. Уравнение поверхности уровня выглядит следующим образом:

f(x,y,z) = C

Наибольшее и наименьшее значение в области

Функция, которая ограничена и дифференцируется в замкнутой области, имеет наибольшее и наименьшее значение либо во внутренних точках этой области, либо на ее границе. Используем пример для рассмотрения алгоритма нахождения наибольшего и наименьшего ее значения.

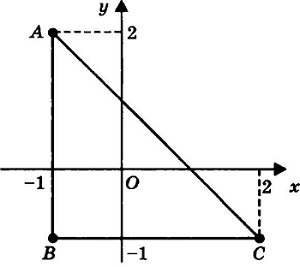
Перед нами функция \(z\;=\;\frac13x^3\;+\;3xy\;+\;\frac13y^3\) в замкнутой области \(х\geq-1,\;у\geq-1,\;х+у\leq1\).

Следующее действие поможет нам определить стационарные точки функции:

\(\frac{dz}{dx}\;=\;x^2\;+\;3y\;,\;\frac{dz}{dy}\;=\;3x\;+\;y^2\;\Rightarrow\left\{\begin{array}{l}x^2\;+3y\;=\;0\\3x\;+\;y^2\;=\;0\end{array}\right.\Rightarrow\;\left\{\begin{array}{l}x^2\;+\;3y\;=\;0\\x\;=\;-\frac{y^2}3\end{array}\;\Rightarrow\;\right.\frac{y^4}9+3y\;=\;0\;\Rightarrow\frac y9(y^3+27)\;=\;0\;\Rightarrow y_{}\;=\;0\;\Rightarrow y_2\;=\;-3\;\Rightarrow\;x_1\;=\;0\;\Rightarrow x_2\;=\;-3\)

Из этого следует, что стационарные точки функции всего две — O (0, 0) и M (-3, -3). При достижении функции наибольшего или наименьшего значения внутри области, это происходит исключительно в стационарных точках, которые принадлежат данной области. В этом случае имеет смысл рассматривать только точку O (0, 0).

Теперь рассмотрим границу области, состоящую из AB, BC и AC. Необходимо взглянуть на каждый участок в отдельности. Если подставить уравнение участка AB границы x = -1 в функцию:

\(z=\frac13y^3-3y-\frac13\) при \(-1\leq y\leq2\)

Тогда предстоит определить наибольшее и наименьшее значение указанной функции одной переменной на этом отрезке.

 \(\frac{dz}{dy}=y^3-3=0\\y_1=\sqrt3\\y_2=-\sqrt3\\y_2\not\in\lbrack-1,2\rbrack\)

Очевидно, что функция принимает наибольшее и наименьшее значение в точке \(y_1 = \sqrt3\), а также на границе отрезка в точках -1 и 2. Из этого следует, что к точке P нужно добавить точки В(-1, -1), K(-1,\(\sqrt3\)) и A(-1, 2).

Уравнение участка BC 

y = -1

Функция на этом участке имеет вид

\(z\;=\;\frac13x^3-3x-\frac13\\-1\leq x\leq2\\\frac{dz}{dx}=x^2-3=0\;\Rightarrow\;x_1=\sqrt3,\;x_2=-\sqrt3\\x_2\;\not\in\lbrack-1,\;2\rbrack\\\)

Из этого следует, что достижение наибольшего и наименьшего значения для функции возможно в точке \(x_1 = \sqrt3\) на границе отрезка в точках -1 и 2. Таким образом к выбранным ранее точкам добавятся еще две: К2(\(\sqrt3\), -1) и С(2, -1)

Уравнение участка AC

x + y = 1 или y = 1 - x

Теперь нужно вновь подставить уравнение этого участка границы в рассматриваемую функцию, учитывая, что \(-1\leq х\leq2\).

\(z\;=\;\frac13x3\;+\;3x(1-x)+\frac13{(1-x)}^3\;=-2x^2\;-\;2x+\frac13\)

\(\frac{dz}{dx}=-4x-2=0\;\Rightarrow\;x=-\frac12\;\Rightarrow\;y=1+\frac12=\frac32\)

Из этого появляется еще одна точка - M (\(-\frac12, \frac32\)).

Теперь предстоит вычислить значение функции в точках A, B, C, K1, K2 K3, O

\(z\;=\;\frac13x^3+3xy+\frac13y^3\)

\(z(A)\;=\;\frac13{(-1)}^3+3(-1)2+\frac132^3=-\frac13-6+\frac83=-\frac{11}3\\z(B)=\frac13{(-1)}^3+3(-1)(-1)+\frac13{(-1)}^3=-\frac13+3-\frac13=\frac73\\z(C)=\frac13{(2)}^3+3(-1)2+\frac13{(-1)}^3+\frac83-6-\frac13=-\frac{11}3\\z(K_1)=\frac13{(-1)}^3+3(-1)\sqrt3+\frac133\sqrt3=-\frac13-3\sqrt3+\sqrt3=-\frac13-2\sqrt3\\z(K_2)=\frac133\sqrt3+3(-1)\sqrt3+\frac13{(-1)}^3=\sqrt3-3\sqrt3-\frac13=-\frac13-2\sqrt3\\z(K_3)=\frac13{(-\frac12)}^3+3(-\frac12)\frac32+\frac13{(\frac32)}^3=-\frac1{24}-\frac14+\frac98=\frac{20}{24}=\frac56\\z(O)=\frac13{(0)}^3+3\cdot0\cdot0+\frac130=0\)

Выберем из полученных значений наибольшее и наименьшее, они же будут наибольшим и наименьшим значением функции на рассматриваемом множестве.

Наименьшее значение функции достигается на точках \(K_1 и K_2 (-\frac13 — \frac2{\sqrt3})\)

Ее наибольшее значение достигается на точке \(B (\frac73)\).

Примеры решения задач

Пример

Найдем область определения функции двух переменных 

\(z=\frac{4+x}{(x+3)(y-5)}\)

Если функция является дробью, то ограничение должно гарантировать, что выполняется следующее условие:

\(x\neq-3,\;y\neq5\)

Область определения функции 

\(D(z)=\{(x,y)\in R^2:x\neq-3,\;y\neq5\}\)

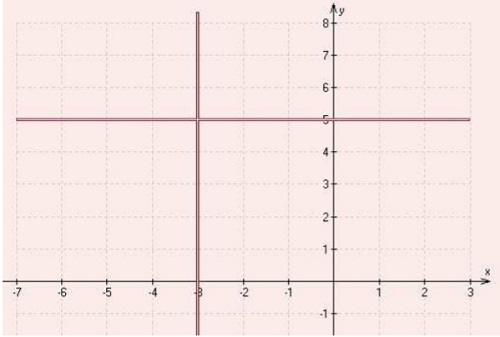
То есть вся числовая плоскость, за исключением точек двух прямых x=-3, y=5

Пример

Необходимо найти область существования функции

\(z=\frac1{\sqrt{4-x^2-y^2}}\)

Для этого решим систему уравнений

\(\left\{\begin{array}{l}y=x^2\\y^2=x,\;x^4=x,\;x^4-x=0,\;x(x-1)(x^2+x+1)=0\end{array}\right.\)

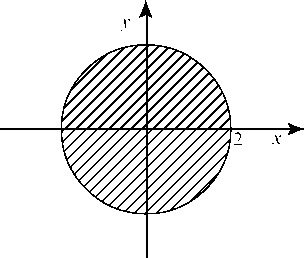
Функция будет иметь действительные значения, если x + у < 4. Этому условию удовлетворяют координаты точек, которые лежат внутри окружности радиуса 2 с центром в начале координат. Тогда область существования функции — это множество точек внутри окружности.