Геометрический смысл дифференциала функции

Что такое дифференциал

Термин дифференциал часто применяют при рассмотрении задач, связанных с построениями и вычислениями функций. Понятие присутствует в нескольких разделах математики, в том числе, дифференциальном и интегральном исчислении, а также обладает прямой связью с определением производной от функции.

В распространенных случаях дифференциал используют, когда расчет предполагает приближенный результат. Кроме того, дифференциал незаменим в процессе анализа погрешностей, которыми характеризуются какие-либо соотношения в уравнениях и измерения.

При необходимости в определении значения дифференциала какой-либо функции следует проанализировать конкретную точку, в которой функция приобретает значение, а также бесконечно минимальное значение, характерное для изменения аргумента.

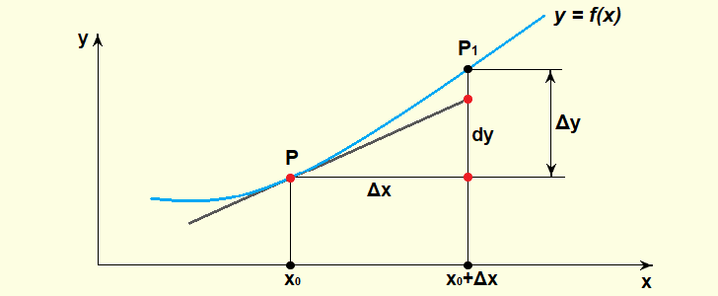
Предположим, что на плоскости отмечена точка х0. Пусть данная точка принадлежит области определения некоторой функции \(f(х)\). Изменение, характерное для х принимает бесконечно маленькое значение. В таком случае дифференциал исследуемой функции можно рассчитать путем умножения величины производной на приращение аргумента этой функции. Для обозначения дифференциала следует использовать \(df(x)\) .

Источник: math24.biz

В чем заключается геометрический смысл дифференциала

Смысл понятия дифференциала с точки зрения геометрии можно объяснить как равенство рассматриваемого дифференциала некоторой функции \(f(х)\) приращению ординаты касательной к графику анализируемой функции. Эта линия пересекает точку на графике, имеющую координаты (х,у), когда координата х меняется на \(\delta х = d(х)\).

Дифференциал играет роль ключевой линейной части некоторой функции по отношению к приращению аргумента. При этом уменьшение значения приращения функции сопровождается увеличением доли приращения, приходящейся на данную линейную часть.

В результате, если изменение х приобретает бесконечно минимальные значения, то справедливо равенство приращения рассматриваемой функции дифференциалу, который для нее характерен. Сформулированное свойство применимо к приблизительным расчетам и определении погрешности измерений.

Примеры решения задач

Решение

Запишем формулу для вычисления частного дифференциала. Озвученное соотношение имеет следующий вид:

\(d _{у}u(х_{0}, у_{0}, z_{0}) = \frac{du}{dy} (х_{0}, у_{0}, z_{0}) \cdot \triangle y\)

Используя представленное соотношение и данные из условия задания, запишем:

\(\frac{du}{dy} = \frac{2у}{ 2 \sqrt{x^{2}+y^{2}+z^{2}}} = \frac{у}{\sqrt{x^{2}+y^{2}+z^{2}}}\)

\(\frac{du}{dy} (-3,4,0) = \frac{4}{ \sqrt{9+16+0}} = \frac{4}{5} =0,8\)

\(d _{у}u (-3,4,0) = 0,8 \cdot \triangle y = 0,8\cdot 0,1 = 0,08\)

Ответ: 0,08

Решение

В первую очередь необходимо вычислить частные производные 1 порядка:

\(f'_x = 2\)

\(f'_y = 3\)

Путем подстановки вычислим значение для полного дифференциала, используя формулу из условия задания:

dz = 2dx + 3dy

Ответ: dz = 2dx + 3dy

Решение:

\(du = f'_x dx + f'_y dy + f'_z dz\)

\(u'_x = yz\)

\(u'_y = xz\)

\(u'_z = xy\)

\(du = yzdx + xzdy + xydz\)

Ответ: \(du = yzdx + xzdy + xydz\)