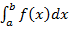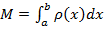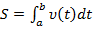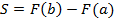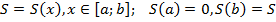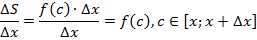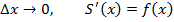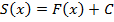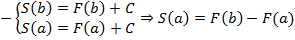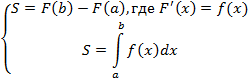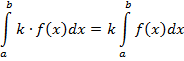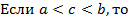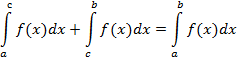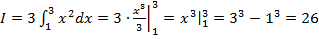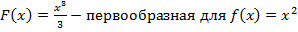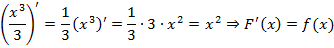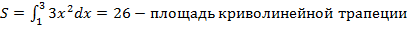Суть геометрического смысла определенного интеграла

Понятие определенного интеграла

В данном выражении:

• a и b являются пределами интегрирования;
• f(x) представляет собой подынтегральную функцию, площадь под которой требуется определить.

 представляет собой площадь криволинейной трапеции подынтегральной функции f(x) в пределах от a до b.

В чем заключается геометрический смысл определенного интеграла

Геометрический смысл определенного интеграла можно записать таким образом:

 

К примеру, масса неоднородного стержня AD будет представлена с помощью равенства:

Скорость перемещения точки вдоль прямой составит:

 

Вычисление определенного интеграла и площади криволинейной трапеции основано на теореме.

Теорема о вычислении определенного интеграла

Теорему можно записать в таком виде:

 

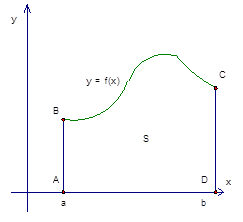
Полученное выражение можно представить с помощью графика:

Доказательство теоремы

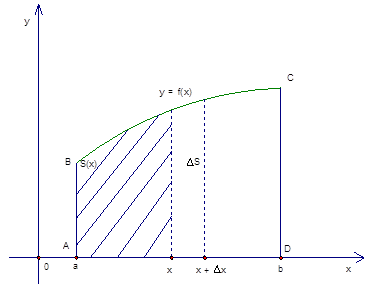
Доказать утверждение можно путем последовательных действий. Сначала требуется на интервале [a;b] зафиксировать х и найти площадь фигуры, которая расположены под кривой на отрезке [a;х]. Таким образом, каждому х соответствует S(х), и получится новая функция:

 

 

Таким образом, площадь криволинейной трапеции будет определяться, как приращение любой первообразной на интервале [a;b].

Формула Ньютона-Лейбница

 

 

Функция y = f (x) является непрерывной в интервале [a;b]. Непрерывную функцию можно представить на графике:

Свойства определенного интеграла

Определенный интеграл обладает рядом характерных свойств:

 

 

          

Как найти площадь криволинейной трапеции при помощи интеграла

В качестве примера можно рассмотреть определенный интеграл:

 

Решение:

В данном случае:

 

Таким образом:

 

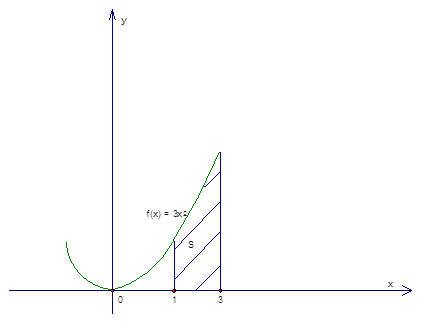
С помощью геометрической интерпретации можно определить площадь криволинейной трапеции:

 

Графически функцию и площадь трапеции можно изобразить, таким образом: