График производной функции
График производной функции — описание
Производная функции — это скорость изменения у при изменении х. При этом одна и та же функция может иметь разное значение производной в разных точках. Обозначается производная следующим образом: \(f'(x)\).
Зависимость производной функции от скорости изменения y заключается в том, что они прямо пропорциональны. Значение производной может быть как больше, так и меньше нуля. Производную функции используют для нахождения точек максимума и минимума функций, а также промежутков их возрастания и убывания.
При помощи вычисления производной и приравнивания её к нулю, возможно найти точки, разбивающие числовую ось на интервалы. Знак производной будет определяться на каждом из найденных интервалов, что позволит сделать в дальнейшем сделать вывод о возрастании или убывании функции.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Производная функции \(f(x)\) в точке \(x_0\) эквивалентна тангенсу угла наклона касательной к графику функции в \(x_0\).
\(f'(x_0)\;=\;tg\alpha\)
Свойства графика
- Производная будет положительной на интервалах возрастания функции. Таким образом, в случае если производная в определенной точке некоего интервала обладает положительным значением, график функции возрастает в обозначенном интервале.
- Производная будет отрицательной на интервалах убывания функции. Таким образом, в случае если производная в определенной точке некоего интервала обладает отрицательным значением, график функции убывает в обозначенном интервале.
- В точке х производная будет равняться угловому коэффициенту касательной к графику функции в обозначенной точке.
- Производная равняется нулю в точках максимума и минимума функции, в тех же случаях параллельности касательной к графику функции и оси \(ОХ\).
Знак производной на интервалах возрастания
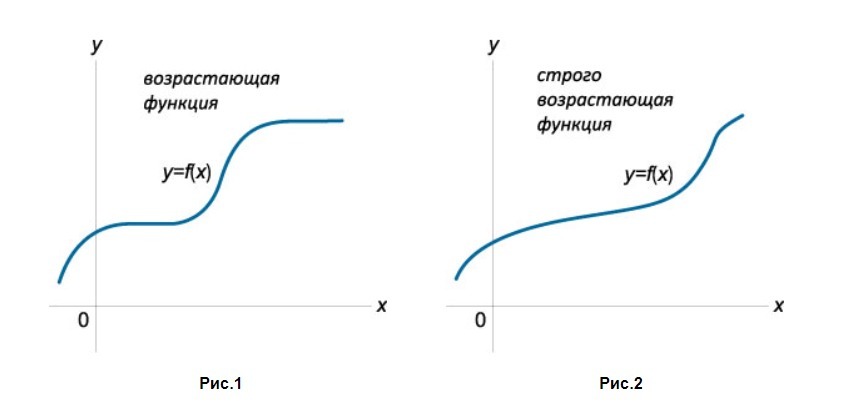
Определим, какая функция называется возвращающей.
\(y = f(x)\) будет возрастать на интервале \(X\), если для любых \(x_1\;\in\;X\) и \(x_2\;\in\;X\), где \(x_2\;>\;x_1\), справедливо неравенство \(f(x_2)\;\geq\;f(x_1)\).
В тех случаях, когда данное неравенство будет соответствовать определению строгого, то есть иметь вид \(f(x_1) < f(x_2)\), функция \(y = f(x)\) будет называться строго возрастающей на интервале \((a, b)\).
На интервалах возрастания производная будет иметь положительный знак. То есть при подстановке значения из интервала в производную, получившееся число будет положительным.
В тех случаях, когда производная функции \(y = f(x)\) положительна для любого x из интервала \(X\), функция возрастает на \(X\).
Знак производной на интервалах убывания
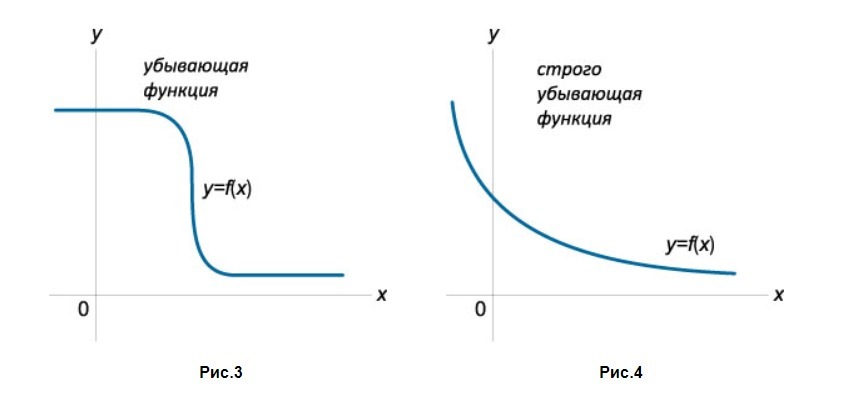
Определим, какая функция называется убывающей.
\(y = f(x)\) будет убывать на интервале \(X\), если для любых \(x_1\;\in\;X\) и \(x_2\;\in\;X\), где \(x_2\;>\;x_1\) справедливо неравенство \(f(x_2)\;\leq\;f(x_1).\)
В тех случаях, когда данное неравенство будет соответствовать определению строгого, то есть имеет вид \(f(x_1) < f(x_2)\), функция \(y = f(x)\) будет называться строго убывающей на интервале \((a, b)\).
На интервалах убывания производная будет иметь отрицательный знак. То есть при подстановке значения из интервала в производную, получившееся число будет отрицательным.
В тех случаях, когда производная функции \(y = f(x)\) отрицательна для любого x из интервала \(X\), функция убывает на \(X\).
Производная и угловой коэффициент касательной
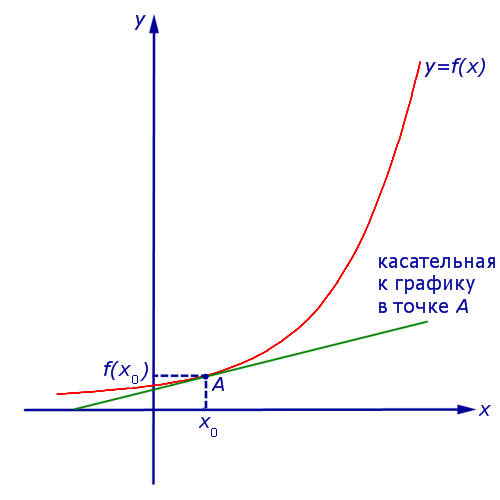
Касательная — прямая, которая имеет на определенном участке единственную общую точку с графиком.
В случае, когда при \(x_1\;\rightarrow\;x_0\) имеется предельное положение секущей графика функции \(y = f(x)\), оно будет носить название касательной к графику функции \(y = f(x)\) в точке \(A\;=\;((x_0;\;f(x_0))\). А значение производной в точке касания \(x_0\) будет эквивалентно угловому коэффициенту касательной.
Угловой коэффициент касательной равен значению производной в точке касания \(x_0\). И в соответствии с тем, что касательная параллельна прямой \(y = -x\), ее угловой коэффициент равен -1.
Геометрический смысл производной состоит в том, что производная в точке \(x_0\) равна угловому коэффициенту касательной к графику функции \(y = f(x)\) в этой точке.
Формула уравнения касательной к графику функции \(y = f(x)\) в точке \(x_0\) выглядит следующим образом:
\(y\;=\;f(x_0)\;+\;f'(x_0)(x\;-\;x_0)\)
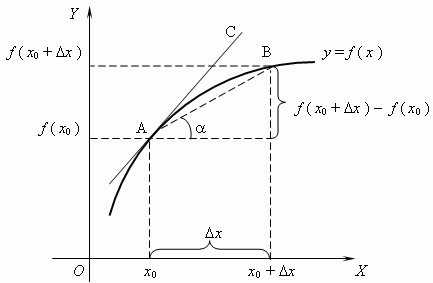
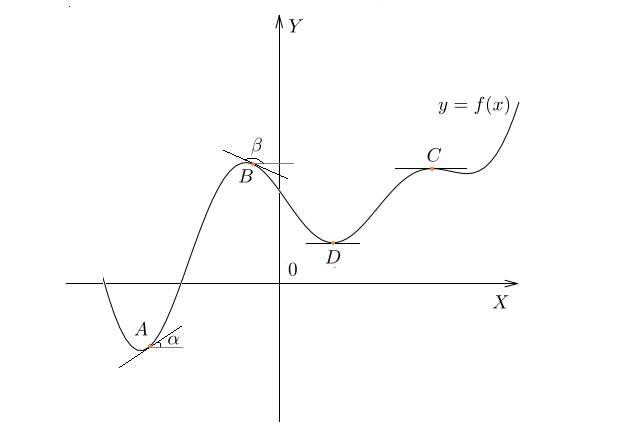
Рассмотрим рисунок графика функции \(y = f(x)\). Очевидно, что для каждой из точек \(A\) и \(B\) графика функции справедливо следующее разностное отношение:
\(\frac{f(x_0+\triangle x)}{f(x_0)\triangle x}=tg\alpha\)
Здесь \(\alpha\) — угол между прямой и осью \(ОХ\), а предел разностного отношения эквивалентен угловому коэффициенту касательной в точке \(A\).
Зафиксируем точку \(A\) и будем продвигать точку \(B\) в направлении к ней. Тогда \(\triangle x\) бесконечно уменьшается и приближается к 0, а секущая \(АВ\) приближается к касательной \(АС\).
Необходимо записать уравнение касательной к графику функции \(y=x+e^{-2x}\), если эта функция параллельна прямой \(y = -x.\)
При условии, что касательная параллельна прямой \(y = -x\), справедливо утверждение об эквивалентности углового коэффициента \(-1\). Этот вывод можно сделать из эквивалентности углового коэффициента касательной значению производной в точке касания \(х_0\). Таким образом \(f'(x0) = -1\).
\(f'(x_0)\;=\;(x_0\;+\;e^{-2x_0})'\;=\;1\;-\;2e^{-2x_0}\\1\;-\;e^{-2x_0}\;=\;-1\\2e^{-2x_0}\;=2\\e^{-2x_0}\;=\;1\\-2x\;=\;0\\x_0\;=\;0\)
Используем уравнение касательной
\(y\;=\;f(x_0)\;+f'(x_0)(x\;-\;x_0)\\x_0\;=\;0;\;f'(x_0)\;=\;-1;\;f(x_0)\;=\;1\\y\;=\;1\;-\;1(x-0)\;=\;1\;-\;x\)
В каких точках производная равна нулю
Производная будет эквивалентна нулю в точках минимума, максимума и перегиба, при параллельной оси \(ОX\) касательной. Рассмотрим следующий рисунок:
Очевидно, что в точках \(C\) и \(D\) касательная горизонтальна, тогда тангенс угла ее наклона будет равняться 0. Отсюда можно сделать вывод, что и производная равна 0. Точка C здесь будет являться точкой максимума. В этой точке возрастание функции изменяется на убывание, как меняется и знак производной — с плюса на минус. Точка \(D\) здесь — точка минимума. В это случае также происходят изменения, но в обратном порядке.
Важно отметить, что производная может не существовать в точке максимума. Такое происходит, если на графике изображен резкий излом, к которому невозможно провести касательную.
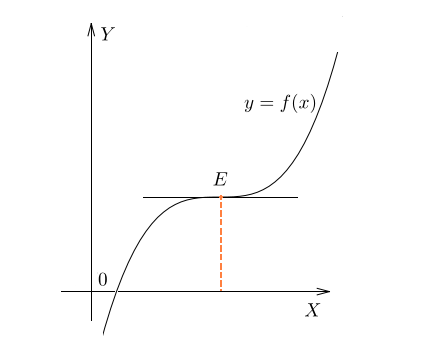
Рассмотрим еще одно изображение функции:
В данном случае производная будет эквивалентна нулю в точке перегиба, так как в точке \(E\) касательная к функции параллельна оси \(ОX\). В этом случае знак производной не будет изменяться, потому что до точки перегиба и после функция возрастает. Знак был и остается положительным.
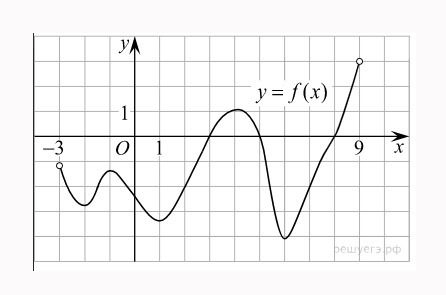
Рассмотрим рисунок, на котором начерчен график функции \(y = f(x)\). График определен на интервале (−3; 9). Необходимо определить количество точек, где производная функции \(f(x)\) эквивалентна 0.
На данном рисунке очевидно, что производная функции f(x) эквивалентна нулю в точках максимума и минимума, то есть в точках −2; −1; 1; 4 и 6. Таким образом производная равна нулю в 5 точках.
Примеры производной на графике функции
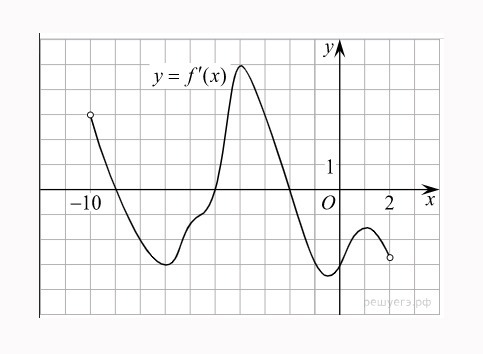
Рассмотрим рисунок.
Рисунок изображает график производной функции \(f(x)\). Функция определена на интервале (-10; 2). Необходимо найти, в скольких точках касательная к графику функции \(f(x)\) будет параллельна прямой \(y = -2x - 11\) или совпадать с ней.
Решение
Используем правило о значении производной, которое в точке касания эквивалентно угловому коэффициенту касательной. Тогда, зная, что касательная параллельна прямой \(y = -2x - 11\) или идентична с ней, можно утверждать, что угловые коэффициенты равны \(-2\).
Теперь необходимо найти число точек, в которых \(f'(x)\;=\;-2\). Искомое значение соответствует числу точек, где график производной пересекается с прямой \(y = -2\). На заданном интервале 5 таких точек.
Ответ: 5.
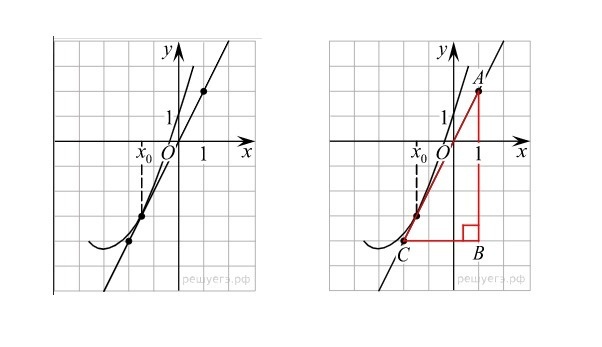
Первый рисунок изображает график функции \(y = f(x)\) и касательную к нему в точке с абсциссой \(x_0\). Необходимо установить значение производной функции \(f(x)\) в точке \(x_0\).
Решение
Используем правило, гласящее, что угловой коэффициент касательной эквивалентен значению производной в точке касания, который в свою очередь эквивалентен тангенсу угла наклона данной касательной к оси абсцисс. На втором рисунке показано, что решить задачу можно с помощью построения треугольника, вершины которого соответствуют точкам A (1; 2), B (1; -4), C(-2; -4). Тогда угол наклона касательной к оси абсцисс можно найти через угол \(ACB\), которому он будет равен:
\(y'(x_0)\;=\;tg\angle ABC\;=\;\frac{AB}{BC}\;=\;\frac{2+4}{1+2}\;=\;2\)
Ответ: 2.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так