Иррациональные числа

Что такое иррациональные числа

Если в ходе решения математической задачи получилась дробь, в которой нельзя полностью разделить числитель на знаменатель, то это иррациональное число.

Существует еще одно условие принадлежности такой дроби к иррациональным величинам. Это отсутствие периодов в наборе цифр после запятой, т.е. нет периодически повторяемой цифровой последовательности.

С таким множеством сталкивались еще математики древних веков. Для них, например, было понятно, что диагональ квадрата нельзя разделить на длину его стороны и получить при этом не бесконечную дробь. Аналогичным образом характеризуется соотношение постоянной π выбранной окружности к диаметру.

Говоря простыми словами, если в обычной десятичной дроби после запятой обнаруживается бесконечное количество цифр и в них отсутствует повторяемость периодов, то это представитель иррационального множества.

Термин, обозначающий данную категорию цифр, произошел в результате сложение двух частей: ratio, что означает «соотношение» и ir, что означает отрицание. В итоге слово «иррациональный» закрепилось за дробями, не способными дать четкое соотношение.

Например, диагональ квадрата, сторона которого равна 1, не может быть представлена рациональным числом, но она имеет определенное числовое выражение. К таким же случаям можно отнести √5, √7, √10. Именно для выражения таких значений введено множество иррациональных чисел, каждое из которых может быть представлено бесконечной непериодической дробью (в отличие от рационального, которое можно представить периодической десятичной дробью).

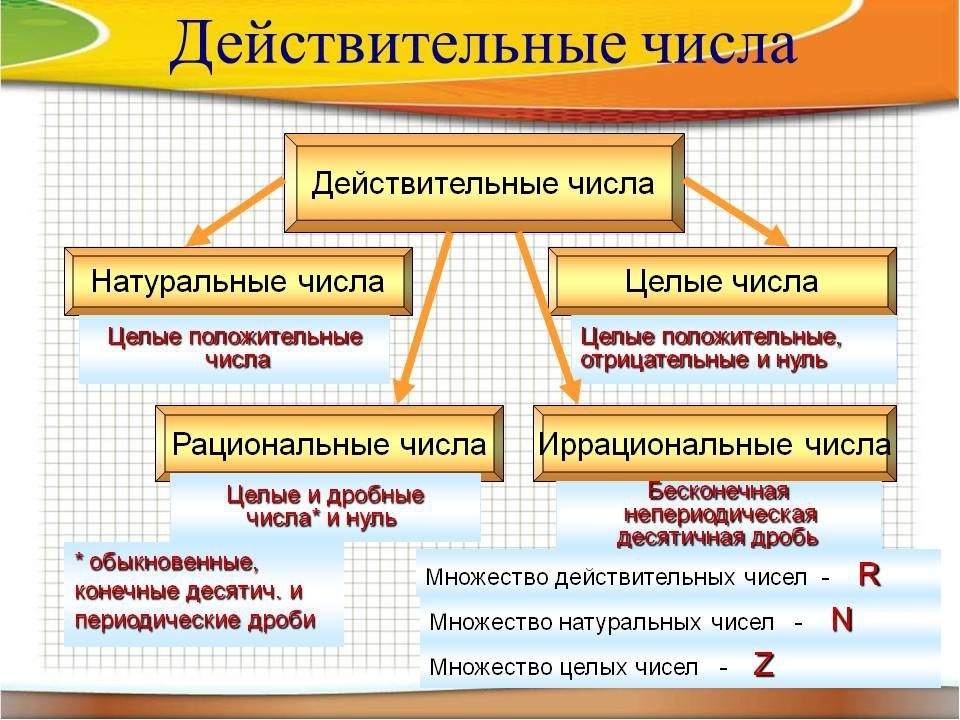
Виды, место в общей классификации, как обозначаются

В арифметической классификации иррациональным числам выделено четкое место, наравне с рациональными, которые делятся на целые и дробные.

Для обозначения множества используют букву I. Его математическое выражение выглядит так: I=R-Q.

Алгебраические и трансцендентные

В алгебре те величины, которые могут являться квадратными корнями с целыми коэффициентами из многочленов, относятся ко множеству алгебраических. Те же, которые не могут выступать в этой роли, образуют другое множество — трансцендентных.

Происхождение термина «трансцендентный» объясняется его переводом с латыни: transcendentis — выходящий за границы. Таким образом, это величины, которые находятся за пределами множества чисел, которые могут стать квадратным корнем с целым коэффициентом из различных многочленов.

О необходимости введения такого множества впервые заговорил в 1775 году Леонард Эйлер. Стоит отметить, что во время его деятельности еще не было известно никаких трансцендентных значений.

Вычислить их пример не удавалось математикам и в последующие много лет. Лишь в 1844 году Ж.Луивилль привел всем их пример. Его теореме досталось лидирующее место в теории диофантовых приближений.

Все числа типа m/n, где n отлично от нуля, а m и n представлены целыми значениями, являются алгебраическими. Для них справедливо равенство: nx-m=0.

К понятию «алгебраические», кроме рациональных, отнесены иррациональные, для которых характерна формула ⁿ√m. При этом m и n представлены целыми числами, а n больше либо равно 2.

При любых действиях с алгебраическими числами (сложение, вычитание, деление либо умножение) результат решения будет алгебраической величиной. Кроме этого, алгебраическими будут корни многочленов, коэффициенты которых также отнесены к этому множеству.

Для чего они используются

В математике использование иррациональных чисел объясняется списком их свойств. Например, возможность точного определения величины, полученной в результате извлечения квадратного корня из 2-х, не всегда нужна. Так, в геометрии измерения длины гипотенузы часто производят приблизительно (1,4, 1,41 и т.д.). Извлечение точного квадратного корня из 2-х понадобится только при работе с абстрактной математической моделью.

Однако такие ситуации в науке существуют. Поэтому существование множества иррациональных чисел оправданно. С помощью них можно высчитать дедекиндово сечение в рациональных числах, у которых отсутствует самое большое в нижнем сегменте и самое малое — в верхнем.

Представители иррациональных значений позволяют уплотнить числовую прямую с нанесенными рациональными значениями, таким образом, что между каждой такой парой можно записать иррациональное.

Например, в результате сложения корня из семи (любой степени) и такого корня из семи, только со знаком минус, получается рациональное число — 0.

Исходя из сказанного, следует сделать вывод, что введение множества иррациональных чисел необходимо для увеличения точности. Например, когда между натуральными числами единицей и двойкой не было промежуточных величин, нужно было ее ввести для расширения диапазона точности.

Как вычислить иррациональное число, действия

Чтобы вычислить иррациональное число проще всего предположить, что оно рациональное и его реально представить в виде дроби p/q, не поддающейся сокращению. В результате преобразующих действий доказывается, что натуральные p и q не являются взаимно простыми. Тогда понятно, что это именно иррациональное значение, а предположение о рациональности взятой дроби ошибочно.

В целом же под понятием «иррациональное» понимается число, записать которое в виде десятичной дроби невозможно. Часть после запятой будет бесконечной:

π =3,14159…;

e =2,7182…;

«золотого сечения» 1,61803398…

При этом степень точности результата зависит от количества знаков, взятых после запятой.

Правда, при описании таких величин чаще используют логарифмы, корни, степени и т.п.

Чтобы в текущий момент определить принадлежность данного числа к категории иррациональных, можно воспользоваться онлайн калькулятором, в котором можно произвести вычисления до оговоренной точности. 

На калькуляторе нужно задать число в виде правильной дроби (по определению, оно рациональное). Исходя из этого, результативным будет определение иррационального компонента для выражений в виде корней (со степенью n).

Получаем:

•  ²√2 = 1,414 (иррациональное);
•  ³√27 = 3 (рациональное);
•  ⁵√147 = 2,713 (иррациональное).

Видим, что, имея дело с квадратными и кубическими корнями, извлекаемая величина может быть рациональной.