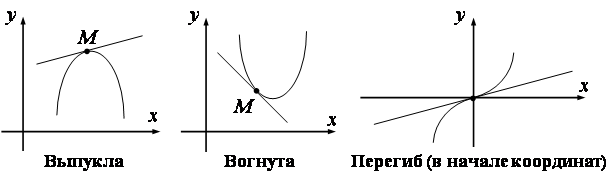Применение производной к исследованию функции
Как применить производную к исследованию функции
Производная функции — это скорость, с которой функция изменяется в зависимости от входной переменной. Другими словами, производная измеряет мгновенный наклон функции в любой заданной точке.
Производная функции \(f(x)\) обозначается как \(f'(x)\) и определяется как предел разности коэффициентов по мере приближения изменения x к нулю:
Формула: \(f'(x) = lim(h -> 0) [f(x + h) - f(x)] / h\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Чтобы найти функцию с помощью производной, необходимо проинтегрировать производную функции. Этот процесс называется антидифференцированием или интегрированием. Интегрирование, по сути, является обратным дифференцированию, поэтому оно позволяет восстановить исходную функцию по ее производной.
Алгоритм нахождения функции с помощью производной:
- Продифференцируйте функцию, чтобы найти ее производную. Например, если функция \(f(x) = x^3 + 2x^2 - 3x\)f, то ее производная \(f'(x) = 3x^2 + 4x - 3\)f'.
- Проинтегрируйте производную, отменив правило мощности. Если \(f'(x) = 3x^2 + 4x - 3, то f(x) = x^3 + 2x^2 - 3x + C\) , где C — постоянная интегрирования. Константа интегрирования возникает потому, что дифференцирование не является обратимым процессом; производная константы всегда равна нулю, поэтому любой постоянный член в исходной функции исчезает при дифференцировании.
- Если у вас есть начальные условия или граничные значения, вы можете использовать их для решения задачи о константе интегрирования. Например, если f(0) = 1, то 1 = 0 + 0 - 0 + C, поэтому C = 1. Исходная функция \(f(x) = x^3 + 2x^2 - 3x + 1\).
Вот несколько примеров решения задач с использованием производных функций:
Найдите наклон касательной к кривой: Если задана функция \(f(x)\), то наклон касательной к кривой в точке x=a определяется производной \(f'(a)\). Например, если \(f(x) = x^2\), то \(f'(a) = 2a\), поэтому наклон касательной к кривой в точке x=2 равен 4.
Найдите мгновенную скорость изменения функции: Если задана функция \(f(x)\), то мгновенная скорость изменения в точке x=a определяется производной \(f'(a)\). Например, если \(f(x) = 3x^2 + 2x + 1, то f'(a) = 6a + 2\), поэтому мгновенная скорость изменения в точке x=3 равна 20.
Найдите максимальное или минимальное значение функции: Чтобы найти максимальное или минимальное значение функции \(f(x)\), сначала найдите ее критические точки, установив производную \(f'(x)\) равной нулю. Затем оцените \(f(x)\) в каждой критической точке и в конечных точках области, чтобы определить максимальное или минимальное значение. Например, если \(f(x) = x^3 - 6x^2 + 9x + 2, то f'(x) = 3x^2 - 12x + 9\). Приравнивание \(f'(x)\) к нулю дает x=1 и x=3, которые являются критическими точками. Оценка при x=1, x=3 и конечных точках области дает \(f(-1)=-4, f(1)=6, f(3)=2 и f(5)=52\). Следовательно, максимальное значение \(f(x)\) равно 52, что происходит при x=5.
Найдите точки перегиба функции: Чтобы найти точки перегиба функции \(f(x)\) , найдите вторую производную \(f''(x)\) и приравняйте ее к нулю, чтобы найти любые точки перегиба. Например, если \(f(x) = x^3 - 3x^2 - 9x + 10, то f''(x) = 6x - 6\). Приравнивание \(f''(x)\) к нулю дает x=1, что является точкой перегиба кривой.
Применение производной
Основные способы использования производной при изучении функций:
- Нахождение наклона касательных линий позволяет нам изучить локальное поведение функции.
- Нахождение критических точек: Критические точки функции — это точки, в которых производная равна нулю или не определена. Эти точки важны для определения местоположения экстремумов и точек перегиба функции.
- Определение интервалов возрастания и убывания позволяет изучить глобальное поведение функции.
- Определение вогнутости и точек перегиба определяет расположение точек перегиба и набросать форму графика функции.
- Нахождение максимального и минимального значений, которые находятся в критических точках или в конечных точках области. Мы можем использовать производную, чтобы определить, является ли критическая точка локальным максимумом или минимумом.
Полная схема исследования функций
Область функции — это множество всех возможных входных значений (также называемых независимой переменной), для которых функция определена. Другими словами, это множество всех значений x, для которых функция дает допустимый результат. Область функции может быть задана явно или неявно, в зависимости от характера функции.
Например, рассмотрим функцию \(f(x) = 1/x\). Знаменатель функции не может быть нулевым, поэтому областью функции являются все действительные числа, кроме x = 0, то есть D = {x ∈ R | x ≠ 0}.
Другой пример - функция \(g(x) = √(x - 2)\). Радиканда (x - 2) должна быть неотрицательной, поэтому областью функции являются все действительные числа, большие или равные 2, т.е. D = {x ∈ R | x ≥ 2}.
Иногда область действия функции неявно определяется контекстом, в котором она используется. Например, в задаче о расстоянии, пройденном автомобилем за время, область функции неявно определяется как множество всех неотрицательных действительных чисел (поскольку время не может быть отрицательным).
Диапазон функции — это множество всех возможных выходных значений, или множество всех значений y, которые может выдать функция, т.е., множество всех значений, которые функция «выдает», когда мы подключаем различные входы из ее области.
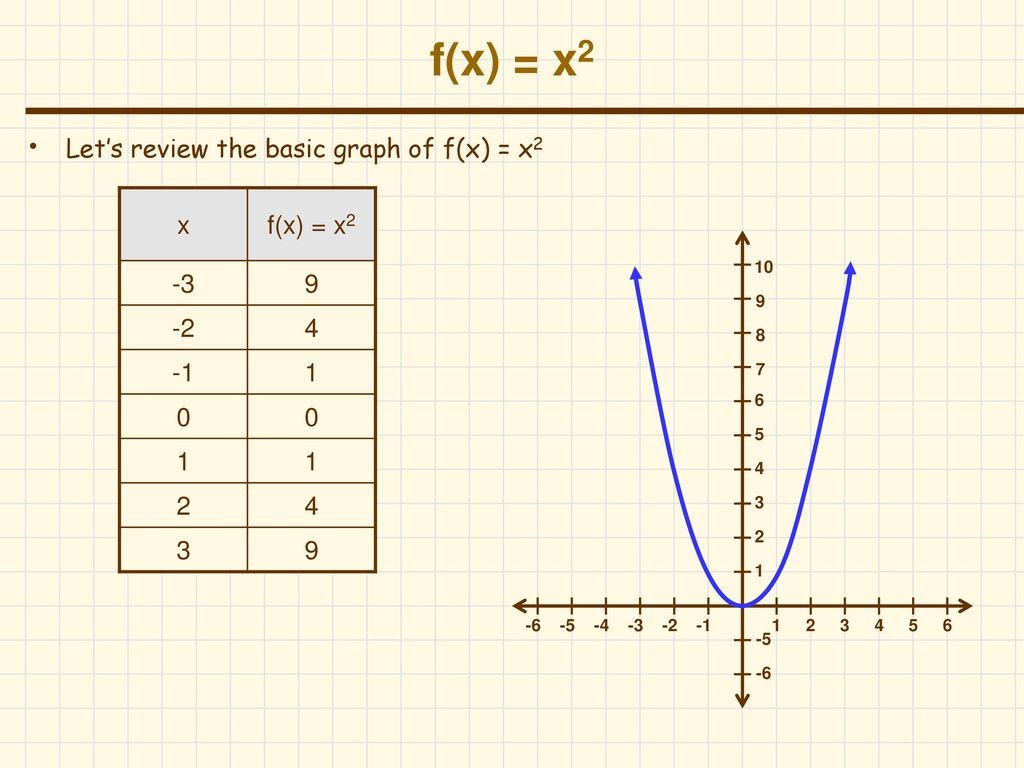
Например, рассмотрим функцию \(f(x) = x^2\). Область этой функции — все действительные числа, так как мы можем подставить любое число, которое захотим, для x. Однако диапазон — это только множество неотрицательных действительных чисел, так как квадрат любого действительного числа всегда неотрицателен.
Симметрия относится к объекту или функции, которые демонстрируют определенный вид баланса или сходства в своей структуре или поведении.
Для функций существует несколько типов симметрии, которые обычно изучаются:
- Равномерная: Считается, что функция \(f(x)\) обладает четной симметрией, если она удовлетворяет свойству \(f(-x) = f(x)\) для всех x в своей области. Геометрически это означает, что график функции симметричен относительно оси y. Примерами четных функций являются \(f(x) = x^2 и f(x) = cos(x)\).
- Нечетная: Функция \(f(x)\) обладает нечетной симметрией, если она удовлетворяет свойству \(f(-x) = -f(x)\) для всех x в своей области. Геометрически это означает, что график функции симметричен относительно начала координат. Примерами нечетных функций являются \(f(x) = x^3 и f(x) = sin(x)\) .
- Периодическая: Функция \( f(x)\) обладает периодической симметрией, если она удовлетворяет свойству \(f(x + T) = f(x)\) для некоторой фиксированной постоянной T и всех x в ее области. Геометрически это означает, что график функции повторяется через каждые T единиц. Примерами периодических функций являются \(f(x) = sin(x) и f(x) = cos(x).\)
Пересечения — это точки, в которых график пересекает ось x или y. Они полезны при анализе поведения функции и поиске важных особенностей ее графика.
- Х-пересечение — это точка, в которой график функции пересекает ось х, что означает, что значение функции в этой точке равно нулю. Чтобы найти х-пересечения функции, мы задаем функцию равной нулю и решаем для значений х. Эти значения представляют собой точки, в которых график пересекает ось х.
- Y-пересечение — это точка, в которой график функции пересекает ось y, а значит, значение функции в этой точке — это y-координата точки. Чтобы найти y-пересечение функции, мы задаем x равным нулю и оцениваем функцию при этом значении. Полученное значение представляет собой точку пересечения графика с осью y.
Асимптоты — это линии, к которым приближается график функции, но никогда не касается их. Они могут быть вертикальными, горизонтальными или косыми (наклонными).
Вот некоторые распространенные типы асимптот:
- Вертикальные возникают, когда функция приближается к вертикальной линии (x = a), но никогда не касается ее. Они могут возникать для рациональных функций, когда знаменатель равен нулю при x = a.
- Горизонтальные возникают, когда функция приближается к горизонтальной линии (y = b) при приближении x к бесконечности или отрицательной бесконечности. Они могут возникать для рациональных функций, когда степень числителя меньше или равна степени знаменателя.
- Косые (наклонные) возникают, когда функция приближается к наклонной прямой (y = mx + b) при приближении x к бесконечности или отрицательной бесконечности. Они могут возникать для рациональных функций, когда степень числителя на единицу больше степени знаменателя.
Условия
Экстремумы и монотонность
Экстремумы — это максимальные и минимальные значения, которых достигает функция в своей области. Они могут возникать либо в критических точках, либо в конечных точках области.
1. Проверка на первую производную предполагает нахождение критических точек функции, то есть точек, в которых производная равна нулю или не определена. Затем анализируем знак производной по обе стороны от каждой критической точки, чтобы определить, является ли она локальным максимумом, локальным минимумом или ни тем, ни другим.
Если в критической точке знак производной меняется с положительного на отрицательный, то это локальный максимум. Если знак меняется с отрицательного на положительный, то это локальный минимум. Если знак не меняется, то это ни максимум, ни минимум.
2. Проверка второй производной предполагает нахождение критических точек функции, а затем анализ вогнутости функции в каждой критической точке с помощью второй производной. Если вторая производная положительна, то критическая точка является локальным минимумом. Если вторая производная отрицательна, то критическая точка является локальным максимумом. Если вторая производная равна нулю, то тест не дает результатов, и нужно использовать другой метод, например, тест на первую производную.
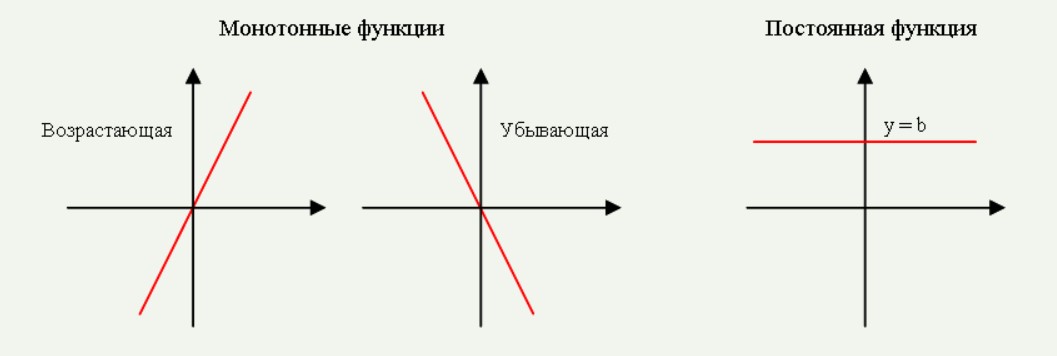
Монотонность относится к поведению функции в отношении ее возрастания или убывания на интервале. Считается, что функция монотонно возрастает, если ее значения увеличиваются по мере увеличения независимой переменной (обычно обозначаемой x) на этом интервале. Аналогично, функция монотонно убывает на интервале, если ее значения уменьшаются с увеличением x на этом интервале. Функция, которая не является ни возрастающей, ни убывающей на интервале, называется немонотонной на этом интервале.
Монотонность функции можно определить, анализируя ее производную. Если производная функции положительна на интервале, то функция монотонно возрастает на этом интервале. Если производная отрицательна на интервале, то функция монотонно убывает на этом интервале. Если производная равна нулю на интервале, то функция может иметь максимум или минимум в этой точке, но это не указывает на монотонность.
Важно отметить, что монотонность функции зависит от рассматриваемого интервала. Функция может быть монотонно возрастающей на одном интервале и монотонно убывающей на другом.
Выпуклость и точки перегиба
Выпуклость относится к форме графика функции. Считается, что функция выпуклая, если ее график выгнут или изогнут вверх, а функция вогнутая, если ее график выгнут внутрь или изогнут вниз. Термин «выпуклость» происходит от того, что график выпуклой функции похож на выпуклую линзу.
Точка перегиба — это точка на графике функции, в которой изменяется вогнутость. Это точка, в которой график меняется с вогнутого вверх (раскрывается вверх) на вогнутый вниз (раскрывается вниз), или наоборот.
График
Построение графика
\(f(x) = x2\) имеет производную \(f(x) = 2x\). Она является функцией общего наклона. Она дает наклон любой линии, касательной к графику f. Например, если нам нужен наклон касательной линии в точке (-2,4), мы оцениваем производную по координате x этой точки и получаем f(-2) = -4. На рисунке слева показано несколько касательных линий, каждая из которых обозначена своим наклоном.
При каждом x график f имеет наклон 1, поэтому при каждом x высота графика \(f'\) также 1.
При каждом x график f имеет наклон -1/2, поэтому при каждом x высота графика \(f' \) также -1/2.
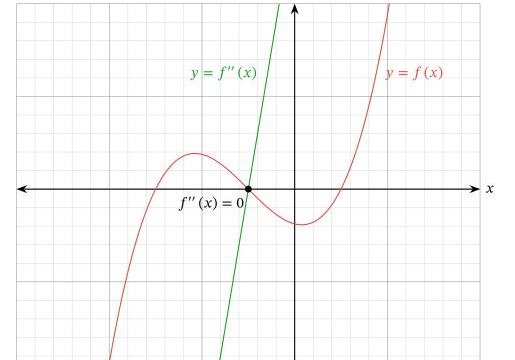
Когда кривая \(y = f'' (x)\) выше x — ось, вторая производная положительна, поэтому f вогнута вверх. Аналогично, когда кривая \(y = f'' (x)\) ниже x — ось, вторая производная отрицательна, поэтому f вогнута вниз.
Примеры решения задач
Нахождение монотонности функции по графику ее производной.
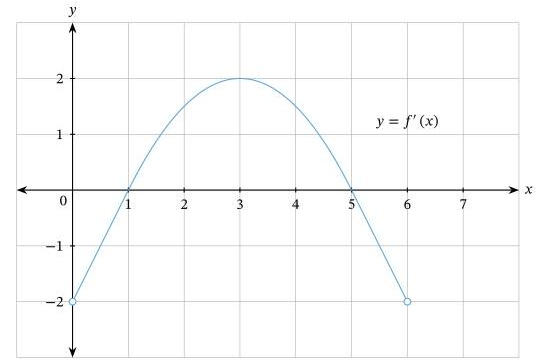
График производной \(f'\)функции fпоказан на рисунке. На каких интервалах f возрастает или убывает?
Ответ: В этом вопросе нам дана кривая \(y = f' (x)\) и попросили найти интервалы, на которых \(f (x)\) увеличивается. Обычно мы смотрим на график и ищем те части графика, где наклон положительный, чтобы увидеть, где функция возрастает, и где наклон отрицательный, чтобы увидеть, где функция убывает. Чтобы ответить на этот вопрос, нам нужно запомнить: наклон функции \(f (x)\) задается \(f' (x)\).
Это означает, что мы также можем увидеть эту информацию на графике \(y = f' (x)\). Производная \(f' (x)\) будет положительным, когда кривая находится выше отметки x и будет отрицательным, когда кривая находится ниже оси x.
Когда x ∈] 1,5 [, что мы имеем \(f′(x) >0\),поэтому наклон \(f (x)\) положительный. Это означает, что для этих значений x наша функция f должна быть возрастающей.
Аналогично, когда x ∈] 0,1 [ или x ∈] 5,6 [, мы видим, что \(f′ (x) <0\)f′, поэтому наклон \(f (x)\) отрицательный для этих значений x, что означает, что f уменьшается на этих интервалах.
Таким образом, мы смогли показать, что f увеличивается на интервале ] 1,5 [ и уменьшается на интервалах ]0,1[ и ]5,6 [.
Стоит отметить, что \(f′ (1) = 0 и f′ (5)=0\) . Поскольку эти значения x являются конечными точками возрастающих или убывающих интервалов, мы технически можем включить эти значения в наш ответ.
На самом деле, в некоторой литературе конечные точки с нулевой производной всегда включаются в интервалы, где функция возрастает или убывает. Включать или не включать конечные точки с нулевой производной в интервалы возрастания или убывания — это личное предпочтение. Кроме того, поскольку наша функция не дифференцируема, когда \(x ≤0 и x ≥6\).
Мы можем просто предположить, что и для этих значений она не увеличивается и не уменьшается.
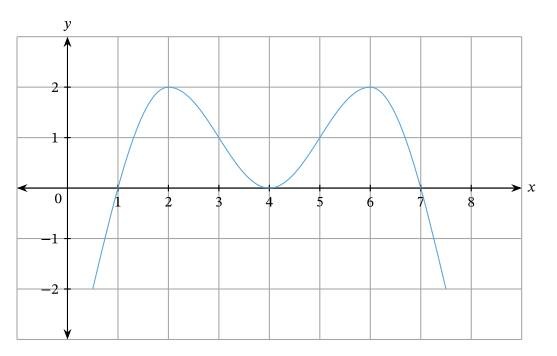
Нахождение x-координат точек перегиба функции по графику ее второй производной. Используйте заданный график функции f′′ для нахождения x-координат точек перегиба из f.
Ответ: Мы хотим найти точки перегиба функции \(f (x)\). Это точки, где \(f (x)\) непрерывна и изменяет вогнутость, либо с вогнутой вверх на вогнутую вниз, либо наоборот.
Мы знаем, что все точки перегиба возникают, когда \(f′′ (x) = 0\) или когда вторая производная не существует. Итак, из нашей диаграммы видно, что это может произойти только тогда, когда x = 1, x = 4 или x = 7.
Однако мы только показали, что наша кривая может иметь точки перегиба при этих значениях x.
Нам все еще нужно проверить, действительно ли это точки перегиба. Для этого нужно проверить, изменяет ли кривая вогнутость при этих значениях x.
Кривая вогнута вверх, если ее вторая производная положительна, и вогнута вниз, если ее вторая производная отрицательна. Нам дан график кривой \(y = f′′ (x)\), поэтому можем определить, когда она положительна или отрицательна, посмотрев, где кривая находится выше или ниже точки оси x.
Теперь видно, что когда x = 1, кривая y = f (x) изменится с вогнутой вниз на вогнутую вверх. Аналогично, когда x = 7, кривая y = f (x) изменится с вогнутой вверх на вогнутую вниз. Таким образом, обе эти точки являются точками перегиба для нашей кривой. Однако мы видим, что вогнутость не меняется с положительной на отрицательную или наоборот в точке x = 4, поэтому это не точка перегиба.
Таким образом, существует две точки перегиба для кривой y = f (x), один, когда x = 1 и другой, когда x =7.
Нахождение вогнутости функции по графику ее производной. График первой производной f' функции f показан на рисунке. На каких интервалах f вогнута вверх или вогнута вниз?
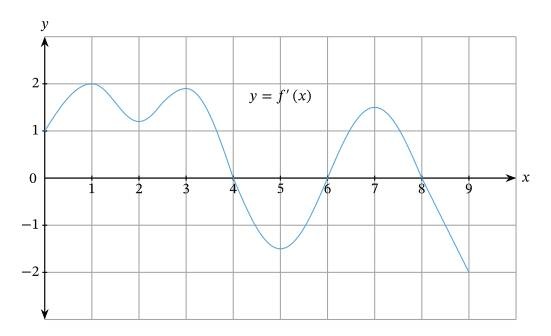
Ответ: Мы хотим определить интервалы, в которых кривая y = f(x) является вогнутой вверх и вогнутой вниз; однако вместо графика этой функции нам дается график ее производной. Поэтому, чтобы ответить на этот вопрос, придется начать с того, чтобы вспомнить связь между производной функции и ее вогнутостью.
Во-первых, кривая вогнута вверх, если ее вторая производная положительна, и вогнута вниз, если ее вторая производная отрицательна.
Это означает, что нужно определить знак второй производной по графику первой производной. Для этого нужно помнить, что если мы продифференцируем первую производную, то получим вторую производную — \(f'' (x)\) — это наклон кривой \(y = f' (x)\).
Поэтому, когда наклон \(y = f' (x)\) положительный, кривая \(y = f(x)\) вогнута вверх, и когда наклон \(y = f' (x)\) отрицательнsq, кривая \(y = f(x)\) вогнута вниз.
Мы можем отметить интервалы, где наклон положительный и отрицательный, на предоставленном нам графике. Мы видим, что f вогнута вверх на ]0,1[, ]2,3[, и ]5,7[ и вогнуты вниз на ]1,2[, ]3,5[, и ] 7,9[/
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так