Как извлечь корень из комплексного числа

Извлечение корня

Не существует однозначного извлечения корня из комплексного числа, так как он имеет то количество значений, которое равно его степени.

Тригонометрическая форма

Если число z представлено в тригонометрической форме \(z=\left|z\right|\cdot\left(\cos\left(ф\right)+i\sin\left(ф\right)\right)\), то значения корня n-ой степени находятся по формуле:

\(\sqrt[n]z=\sqrt[n]{\left|z\right|}\cdot(\cos\left(\frac{ф+2nk}n\right)+i\sin\left(\frac{\;ф+2nk}n\right)).\)

Где |z| — модуль комплексного числа, ф — аргумент, k — параметр, значения у которого 0,1,2…n-1.

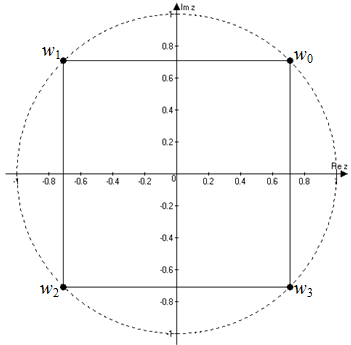
Если посмотреть на извлечение корня n-ой степени с точки зрения геометрии, центр окружности с радиусом \(\sqrt[n]z\) расположен в точке О (0; 0), а все полученные значения, расположенные на ней, образуют правильный n-угольник (как это представлено на чертеже выше).

Алгебраическая форма

Если из данного числа z нужно извлечь корень n-ой степени, а он представлен в алгебраической или показательной форме, необходимо выполнить извлечение по пунктам:

1. Представить число в тригонометрической форме: вычислить модуль \(\left|z\right|\) и аргумент (ф).
2. Полученные значения применить в тригонометрической форме: \(z=\left|z\right|\cdot\left(\cos\left(ф\right)+i\sin\left(ф\right)\right).\)
3. Извлечь корни по формуле, приведенной выше.

Алгоритм вычисления квадратного и кубического корня

Задача на кубический корень

Задача:

Извлечь кубический корень\( \sqrt[3]z\), где \(z=\frac12+\frac12\cdot i\) в алгебраической форме.

Решение:

Вспомним, что тригонометрическая форма записи комплексного числа выглядит так: \(z=\left|z\right|\cdot\left(\cos\left(ф\right)+i\sin\left(ф\right)\right).\)

По условию мы знаем, что \(a=\frac12\) и \(b=\frac12.\)

Можем вычислить исходное значение комплексного числа:

\(r=\sqrt{\left(\frac12\right)^2+\left(\frac12\right)^2}=\sqrt{\frac14+\frac14}=\sqrt{\frac12}=\frac1{\sqrt2}.\)

Теперь посчитаем аргумент исходного комплексного числа:

\(ф=arg(z)=arc\tan\left(\frac{1/2}{1/2}\right)=arc\tan\left(1\right)=\frac\pi4.\)

Далее подставим значения в тригонометрическую форму записи и получим:

\(z=\frac{\sqrt2}2\cdot\left(\cos\left(\frac\pi4\right)+i\sin\left(\frac\pi4\right)\right).\)

Мы знаем, что корнем n-ой степени некоторого числа \(z=\left|z\right|\cdot\left(\cos\left(ф\right)+i\sin\left(ф\right)\right)\) является комплексное число, определяемое следующим равенством:

\(\sqrt[n]z=\sqrt[n]{\left|z\right|}\cdot(\cos\left(\frac{ф+2nk}n\right)+i\sin\left(\frac{\;ф+2nk}n\right)).\)

Воспользуемся этой формулой:

Для k=0: \(w_1=\sqrt[3]z=\sqrt[3]{\frac2{\sqrt2}}\cdot\left(\cos\left(\frac\pi{12}\right)+i\cdot\sin\left(\frac\pi{12}\right)\right).\)

Для k=1 будет справедливо уравнение:

\(x w_2=\sqrt[3]z=\sqrt[3]{\frac2{\sqrt2}}\cdot\left(\cos\left(\frac{\pi/4+2\pi}3\right)+i\cdot\sin\left(\frac{\pi/4+2\pi}3\right)\right)=\sqrt[3]{\frac2{\sqrt2}}\cdot\left(\cos\left(\frac{3\pi}4\right)+i\cdot\sin\left(\frac{3\pi}4\right)\right).\)

Для k=2:

\(w_3=\sqrt[3]z=\sqrt[3]{\frac2{\sqrt2}}\cdot\left(\cos\left(\frac{\pi/4+4\pi}3\right)+i\cdot\sin\left(\frac{\pi/4+4\pi}3\right)\right)=\sqrt[3]{\frac2{\sqrt2}}\cdot\left(\cos\left(\frac{17\pi}{12}\right)+i\cdot\sin\left(\frac{17\pi}{12}\right)\right).\)

Задача на квадратный корень 

Задача:

Извлечь корень \(\sqrt z\)  для заданных комплексных чисел в показательной форме:

\(z=3\cdot e^{\frac\pi3\cdot i}.\)

Решение:

Определим значение модуля и аргумента в тригонометрической форме записи: \(z=\left|z\right|\cdot\left(\cos\left(ф\right)+i\sin\left(ф\right)\right):\)

r=3, \(ф=\frac\pi3.\)

Подставляем ф в равенство: \(z=3\cdot\left(\cos\left(\frac\pi3\right)+i\sin\left(\frac\pi3\right)\right).\)

Воспользуемся формулой \(\sqrt[n]z=\sqrt[n]{\left|z\right|}\cdot(\cos\left(\frac{ф+2nk}n\right)+i\sin\left(\frac{\;ф+2nk}n\right)).\)

Для k=0 справедливо уравнение:

\(w_1=\sqrt z=\sqrt3\cdot\left(\cos\left(\frac\pi6\right)+i\sin\left(\frac\pi6\right)\right);\)

Для k=1: \(w_2=\sqrt z=\sqrt3\cdot\left(\cos\left(\frac{\pi/3+2\pi}2\right)+i\sin\left(\frac{\pi/3+2\pi}2\right)\right)=\sqrt3\cdot\left(\cos\left(\frac{7\pi}6\right)+i\sin\left(\frac{7\pi}6\right)\right).\)