Четыре замечательные точки треугольника

Что такое замечательные точки треугольника

Всего замечательных точек четыре. Две из них открыл Евклид, вписывая в треугольник окружности, третья, точка пересечения медиан, обнаружена Архимедом. Четвертая, в которой пересекаются высоты треугольника, не упоминалась в трудах Евклида, но описывалась в трудах его современников. Возможно, Евклид и Архимед просто упорядочили и записали доказательства теорем, известных задолго до них.

Особенность замечательных точек в том, что они в любом треугольнике являются пересечением трех линий, при этом их свойства не меняются:

• биссектрисы пересекаются в центре вписанного круга;
• перпендикуляры от середин сторон пересекаются в центре описанного круга;
• высоты пересекаются в ортоцентре, точки, симметричные ортоцентру относительно сторон треугольника, находятся на описанном круге;
• медианы пересекаются в барицентре (он же центроид, или геометрический центр).

В XVIII веке математик Леонард Эйлер, исследуя геометрию треугольников, доказал, что три из этих точек — ортоцентр, барицентр и центр описанного круга — всегда расположены на одной линии. Она называется прямой Эйлера. Точки стали называть «замечательными» или «особенными».

Четыре замечательные точки треугольника

Точка пересечения медиан треугольника

В ней находится центр тяжести однородной треугольной пластины, также она является средним арифметическим положений всех точек треугольника.

Доказательство

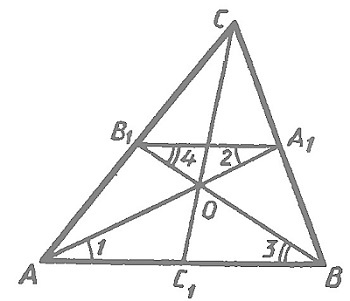
Обозначим точку пересечения медиан О и проведем среднюю линию треугольника \(А^1В^1\).

Отрезок \(А_1В_1\) параллелен \(АВ\), поэтому углы 1, 2, 3 и 4 равны друг другу. Таким образом, треугольники \(АОВ\) и \(А_1ОВ_1\) подобны по двум углам, и их стороны пропорциональны. \(АВ = 2А_1В_1\), значит, \(АО = 2А_1О\) и \(ВО = 2В_1О\), а точка О разделяет медианы на отрезки с отношением 2:1, считая от вершин. Аналогично она делит медиану \(СС_1\).

Точка пересечения биссектрис треугольника

Точка пересечения трех биссектрис расположена на равном расстоянии от всех сторон треугольника и находится в центре вписанного в треугольник круга.

Доказательство

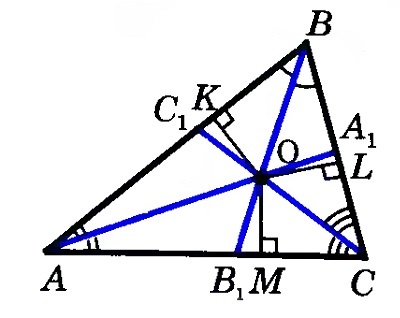
Проведем из точки пересечения биссектрис \(АА_1\) и \(ВВ_1\) отрезки \(ОК\), \(ОL\) и \(ОМ\), перпендикулярные трем сторонам треугольника.

Согласно теореме о равной удаленности точек биссектрисы от сторон угла, ОК = ОМ и ОК = ОL. Соответственно, ОМ = ОL, точка О находится на равном расстоянии от сторон угла АСВ и расположена на биссектрисе. Таким образом, все три биссектрисы пересекутся в одной точке.

Точка пересечения серединных перпендикуляров треугольника

Линии, проходящие через середины сторон треугольника перпендикулярно к ним, пересекаются в центре круга, описанного вокруг треугольника. В остроугольном треугольнике точка пересечения перпендикуляров расположена внутри него, в тупоугольном — снаружи. Если треугольник прямоугольный, точка находится на гипотенузе.

Доказательство

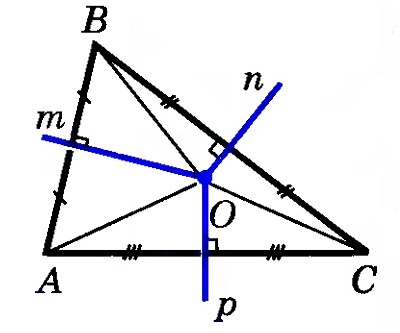
Изобразим внутри треугольника АВС перпендикуляры m и n, отметим точку их пересечения О. 

Согласно теореме о равной удаленности серединных перпендикуляров от концов отрезка, ОВ = ОА и ОВ = ОС. Соответственно, ОА = ОС, и точка О находится на одинаковом расстоянии от точек А и С. Таким образом, серединный перпендикуляр р к отрезку АС тоже будет проходить через точку О, и все три перпендикуляра пересекутся в одной точке.

Точка пересечения высот треугольника

Высоты или их продолжения могут пересекаться как внутри треугольника, если он остроугольный, так и вне его, если он тупоугольный. Если треугольник прямоугольный, тогда ортоцентр совпадает с вершиной прямого угла.

Доказательство

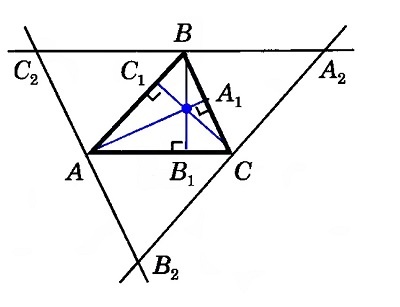
Изобразим произвольный треугольник \(АВС\) и прямые \(AA_1\), \(BB_1\) и \(СС_1\), содержащие его высоты. Проведем через каждую вершину прямые, параллельные противоположным сторонам треугольника, получив треугольник\( A_2B_2C_2\). Точки А, В и С окажутся серединами его сторон.\( АВ = A_2C = В_2C\), так как эти отрезки являются противоположными сторонами параллелограммов \(АВА_2С\) и \(АВСВ_2\). Соответственно, \(С_2А = АВ_2\) и \(С_2В = ВА_2\).

Из построения следует, что отрезок \(СС_1\) перпендикулярен \(А_2В_2\), \(АА_1 \perp В_2С_2\) и \(ВВ_1 \perp А_2С_2\). Следовательно, прямые \(АА_1\), \(ВВ_1\) и \(СС_1\) — серединные перпендикуляры сторон треугольника \(А_2В_2С_2\), которые пересекутся в одной точке.

Примеры решения задач

Задача 1

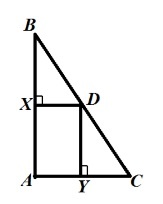
Серединные перпендикуляры к сторонам АВ и АС треугольника АВС пересекаются в точке D, лежащей на стороне треугольника ВС. Докажите, что точка D — середина стороны ВС.

Решение

Изобразим треугольник АВС.

Все серединные перпендикуляры должны пересекаться в одной точке, если два из них уже пересеклись, третий тоже должен проходить через точку D. Таким образом, точка D является основанием третьего серединного перпендикуляра и расположена посередине стороны ВС.

Задача 2

Биссектрисы \(AA_1\) и \(BB_1\) треугольника АВС пересекаются в точке D. Найдите углы АСD и ВСD, если известно, что угол АDB составляет \(136^\circ\).

Решение

Поскольку биссектрисы пересекаются в точке D, луч СD является биссектрисой. Тогда

\(\angle АСD\;=\;\angle BCD\;=\;\frac{\angle C}2\;=\;\frac{180^\circ\;-\;\angle A\;-\;\angle B}2\;=\;90^\circ\;-\;\frac{\angle A}2\;-\;\frac{\angle B}2\;=\;90^\circ\;-\;(180^\circ\;-\;\angle ADB)\;=\;\angle ADB\;-\;90^\circ\)

\(\angle АСD\;=\;\angle BCD\;=\;136^\circ\;-\;90^\circ\;=\;46^\circ\)