Как найти среднюю линию трапеции

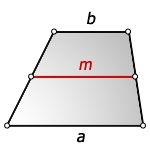
Средняя линия трапеции – что это?

Свойства

1. Параллельна обоим основаниям трапеции.
2. Вычисляется как половина суммы оснований.
3. Разбивает трапецию на две, площади которых соотносятся как \(\frac{S_1}{S_2}=\frac{3\,BC+AD}{BC+3\,AD}\)

Как вычислить, основные формулы

Через основания

\(m=\frac{a+b}2\)

Где \(a\) – нижнее основание, \(b\) – верхнее, \(m\) – средняя линия.

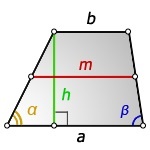
Через основание, высоту и углы при нижнем основании

\(m=a-h\times\frac{ctg\alpha+ctg\beta}2\)

\(m=b+h\times\frac{ctg\alpha+ctg\beta}2\)

Где \(a\) – нижнее основание, \(b\) – верхнее, \(m\) – средняя линия, \(h\) – высота, \(\alpha,\beta\) – углы при нижнем основании.

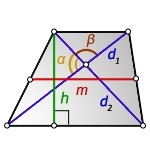
Через диагонали, высоту и угол между диагоналями

\(m=\frac{d_1d_2}{2h}\times\sin\alpha=\frac{d_1d_2}{2h}\times\sin\beta\)

Где \(a\) – нижнее основание, \(b\) – верхнее, \(m\) – средняя линия, \(h\) – высота, \(\alpha,\beta\) – углы между диагоналями, \(d_1\), \(d_2\) – диагонали трапеции.

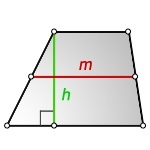
Через площадь и высоту

\(m=\frac{{}_S}h\)

Где \(h\) – высота трапеции, \(m\) – средняя линия, \(S\) – площадь.

Примеры задач

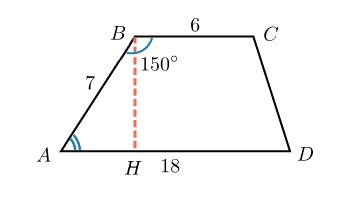
Задача 1

Найдите площадь трапеции, если большее основание равно 18, меньшее 6, боковая сторона равна 7. Угол между боковой стороной и одним из оснований 150 градусов.

\(\angle ABC\) и \(\angle BAH\) односторонние \(\Rightarrow \angle ABC+\angle BAH\;=\;180^\circ \Rightarrow \angle BAH\;=\;30^\circ\)

Рассмотрим \(\angle ABH\)

\(BH=\frac12AB=3,5\)

\(S_{ABCD}=\frac{AD+BC}2\times BH=\frac{6+18}2\times3,5=42\)

Ответ: 42

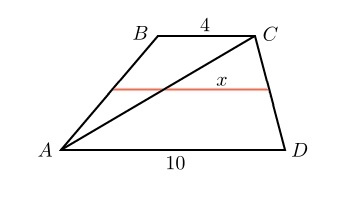
Задача 2

Основания трапеции равны 4 и 10. Чему равен больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей?

Средняя линия трапеции ABCD так же является средней линией треугольников ABC и ACD т.к. проходит через середину одной стороны и параллельна основанию. Значит, из треугольника ACD x = 5.

Ответ: 5

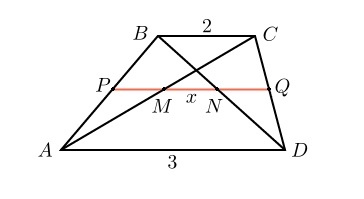
Задача 3

ABCD – трапеция, BC = 2, AD = 3, PQ – средняя линия, BD и AC – диагонали. Найти MN.

\(PQ=\frac{BC+AD}2=2,5\)

Отрезок MN лежит на средней линии трапеции. Докажем: PM и NQ средние линии треугольников ABC и BCD, значит M и N середины соответственно AC и BD. Из треугольника ABC находим длину PM = 1, из треугольника BCD находим NQ = 1, следовательно MN = 2,5 - 1 - 1 = 0,5

Ответ: 0,5